Квантование
1.4. Дискретизация и квантование Как уже отмечалось ранее, для описания различных информационных объектов используются различные функции времени. К ним относятся: 1. Непрерывная функция непрерывного аргумента t (рис. 1.7).
Функция в любой из бессчетного множества моментов времени из конечного интервала времени (t0,tn) может принимать любое значение из бесконечного множества значений, расположенных в конечном интервале (xmin, xmax).
2. Непрерывная функция дискретного аргумента t (рис. 1.8).
Функция может принимать любые значения из бесконечного множества значений, расположенных в конечном интервале (xmin, xmax), но только в фиксированные, наперед заданные моменты времени tk, k=0,1,2,...,n.
3. Дискретная функция непрерывного аргумента t (рис. 1.9).
Значения, которые может принимать функция, образуют дискретный конечный ряд значений, расположенных в интервале (xmin, xmax). Значения аргумента t могут быть любыми в интервале (t0,tn).
4. Дискретная функция дискретного аргумента t (рис. 1.10).
Значения, которые могут принимать аргумент t и функция x(t), образуют конечные дискретные ряды, заполняющие соответствующие интервалы (t0,tn) и (xmin, xmax).
Во многих случаях переход от непрерывного сообщения (сигнала) к дискретному осуществляется специально, поскольку это обеспечивает значительные преимущества при передаче, обработке и хранении информации. В связи с тем, что каждому из дискретных значений конечного множества можно сопоставить число, возникает возможность перейти к цифровому представлению информации, что позволит использовать ЭВМ при ее обработке. Для выполнения этого перехода над непрерывной функцией непрерывного аргумента осуществляются преобразования, называемые квантованием по времени или дискретизацией и квантованием по уровню. В дальнейшем во избежание путаницы под дискретизацией будем понимать квантование по времени, а квантование по уровню будем называть просто квантованием.
1.4.1. Дискретизация
Дискретизация сводится к замене непрерывной по аргументу функции, функцией дискретного аргумента. В результате непрерывная функция отображается конечным числом ее мгновенных значений, взятых через определенные (равные или неравные) промежутки времени Dt. Таким образом, дискретизация представляет собой по сути разложение непрерывной функции на совокупность составляющих ее элементарных функций. Для решения этой задачи используется упомянутое ранее обобщенное преобразование Фурье. Примером ортогонального базиса, кроме рассмотренных ранее гармонических функций, являются функции отсчета Котельникова. Наличие разнообразных базисов в различных областях (частотной и временной) говорит о возможности различных спектральных представлений процессов. Однако при любом из них возникает вопрос о возможности сколь угодно точного восстановления мгновенных значений процесса, исходя из отсчетных или выборочных значений, взятых через определенные интервалы. Дискретизация должна производиться так, чтобы по отсчетным значениям или коэффициентам разложения можно было получить воспроизводящую функцию, которая с заданной точностью отображает исходную функцию. Восстановление непрерывной функции по конечному числу ее значений на конечном интервале времени T=(t0,tn) приводит к погрешности, зависящей от числа взятых значений этой функции на этом интервале, т.е. от частоты дискретизации и от выбранного способа восстановления (интерполяции). Таким образом, при дискретизации приходится решать вопрос о том, как часто следует производить отсчеты функции, т.е. каков должен быть шаг дискретизации Dt или частота дискретизации f=1/Dt. При малом Dt количество отсчетов на интервале Т будет больше, точность воспроизведения - выше, но увеличится и количество информации, которое нужно хранить, передавать, обрабатывать. При большом Dt соответственно наоборот. Оптимальной является такая дискретизация, которая обеспечивает восстановление исходной функции с заданной точностью при минимальном количестве отсчетов. В этом случае все отсчеты существенны для восстановления исходной функции. В случае неоптимальной дискретизации, кроме существенных, производятся и избыточные отсчеты. Эти отсчеты не нужны для восстановления исходной функции с заданной точностью. Наличие избыточной информации нежелательно при ее передаче, обработке и хранении, так как требует больших ресурсов. Устранение этой избыточности может производиться в процессе дискретизации, в связи с чем дискретизацию можно рассматривать не только как операцию по преобразованию непрерывного сообщения в дискретное, но и как один из методов устранения избыточности. Методы дискретизации и восстановления непрерывных функций классифицируются по следующим основным признакам: а) регулярность отсчетов, б) критерии оценки точности дискретизации и восстановления, в) вида базисной функции. Регулярность отсчетов в многом предопределяет степень устранения избыточности и сложность устройств дискретизации и восстановления. В соответствии с этим признаком можно выделить равномерную и неравномерную дискретизации. Дискретизация называется равномерной, если Dt =const на всем интервале Т. Величина Dt выбирается на основе априорных сведений о характере дискретизируемой функции. Равномерная дискретизация применяется достаточно широко из-за простоты алгоритмов и аппаратуры для ее реализации. Однако при ее использовании возможна значительная избыточность отсчетов. Дискретизация называется неравномерной, если Dt =var. Выделяются два вида неравномерной дискретизации: адаптивная и программная. При адаптивных методах дискретизации Dt изменяется в зависимости от текущего изменения значений дискретизируемой функции. При программной дискретизации Dt изменяется в соответствии с заранее составленной на основе априорных сведений о поведении дискретизируемой функции программой. В качестве критериев оценки точности дискретизации и восстановления чаще других используются следующие критерии: а) наибольшего отклонения, б) среднеквадратический, в) вероятностный, г) интегральный. Все эти критерии предлагают метод оценки отклонения воспроизводимой функции от исходной (т.е. ошибки дискретизации) на каждом из интервалов дискретизации. Если максимальная величина ошибки дискретизации задана, то эти критерии позволяют выбрать величину интервала дискретизации Dt, который обеспечить требуемую точность воспроизведения. Существуют два способа воспроизведения исходного сигнала: воспроизведение с экстраполяцией и воспроизведение с интерполяцией. Методы дискретизации с экстраполяцией воспроизводящей функции не требуют задержки сигнала в пределах интервала дискретизации, т.е. могут использоваться в системах, работающих в реальном масштабе времени. Дискретизация с интерполяцией требует задержки сигнала на интервал интерполяции. Выбор системы базисных функций определяется, с одной стороны, требуемой точностью восстановления, с другой - требованиями ограничения сложности устройств и программ дискретизации и восстановления. Требованию простоты нахождения коэффициентов разложения прежде всего отвечают степенные алгебраические полиномы. Использование в качестве базисных ортогональных систем функций в ряде случаев оказывается целесообразным, так как для такой системы относительно просто вычисляются коэффициенты разложения, и вычисление их включает операцию интегрирования сигнала, что положительно сказывается на помехоустойчивости алгоритма дискретизации. Задача оптимального выбора конкретного узкого класса базисных функций может решаться лишь при наличии значительной априорной информации о характере дискретизируемой функции. Так, например, если известно, что сигналы являются периодическими, то поиск базисных функций следует направит в класс гармонических функций. Тот факт, что функция времени, отображающая непрерывной сообщение или сигнал, является произвольной и случайной, означает, что она может иметь временные изменения любой скорости - от самых медленных до бесконечно быстрых скачкообразных изменений. Это, в свою очередь, означает, что такая функция имеет бесконечный спектр. Реальные сообщения обладают спектром, основная часть энергии которых сосредоточена в ограниченной полосе частот. Это обусловлено тем, что устройства, формирующие и преобразующие сообщения и сигналы, обладают конечной ограниченной полосой пропускания. Функции, описывающие такие реальные процессы, называют функциями с ограниченным или финитным спектром. Для таких функций сформулирована и доказана теорема Котельникова, суть которой состоит в том, что функцию s(t) с финитным спектром можно точно восстановить по ее отсчетам s(kDt), взятым через интервалы времени Dt=1/2fв, где fв - верхняя частота спектра функции. Это осуществляется с помощью разложения функции в ряд Котельникова Функции
Рис. 1.11
Свойства функции отсчетов: 1) в моменты времени t=kDt, где k - любое целое число, jk достигает своего максимального значения равного единице; 2) в моменты времени t=nDt, где n - любое целое число, причем n¹k, jk =0; 3) функции отсчетов ортогональны на бесконечно большом интервале времени. Теорема Котельникова обобщается и на случайные процессы. В этом случае она формулируется следующим образом: «Для случайного процесса X(t) с финитным спектром ряд Котельникова Фундаментальное значение теоремы Котельникова состоит в том, что она, во-первых, позволяет заменить исследование непрерывных процессов более простой задачей исследования дискретных процессов. Во-вторых, она позволяет наряду с частотным представлением процессов (разложение в гармонический ряд Фурье, спектральные функции) применять и временное представление - разложение во временной ряд. Полезно сопоставить вид функции отсчетов и получаемое по теореме Котельникова значение Dt с результатами рассмотрения параметров квазибелого шума. Из этого сопоставления можно сделать вывод о том, что шаг дискретизации Dt не должен быть больше интервала корреляции tк дискретизируемого процесса. Однако применение этой теоремы встречает некоторые трудности. Строго говоря, функция с ограниченным спектром не ограничена (не финитна) во времени и, наоборот, финитная функция времени имеет неограниченный спектр. На практике часто приходится иметь дело с сообщениями и сигналами конечной длительности, энергия или мощность которых почти полностью сосредоточена в интервале времени от Т1 до Т2 и в полосе частот DF = fв - fн. Слово «почти» оправдывает применение к этим объектам теоремы Котельникова и позволяет представлять их не бесконечным рядом, а конечной суммой. Естественно, такое представление уже не является точным и выполняется с некоторой погрешностью. Будем полагать, что вся энергия сигнала содержится в полосе частот до fв, а все отсчеты за пределами интервала (Т1, Т2) равны нулю. Тогда Ограничение членов ряда конечным числом приводит к появлению ошибки, абсолютное значение которой равно Очень полезной и более простой формулой для определения допустимой величины шага дискретизации Dt при заданной погрешности Dt для стационарного случайного процесса X(t) является формула Не смотря на наличие указанной погрешности, достоинство такого преобразования состоит в переходе от бесконечномерного пространства к конечномерному пространству сигналов, т.е. сигналов, финитных и по спектру и по времени. Размерность этого пространства определяется числом элементов суммы членов ряда, которое равно Эту величину B=2DFT называют базой сигнала. Физически она указывает на количество отсчетов, необходимых для описания сигнала Обобщая сказанное о дискретизации можно заключить: 1. Представление процесса в виде разложения по ортонормированному базису называется обобщенным преобразованием Фурье. Энергия сигнала равна сумме энергий всех элементов обобщенного ряда Фурье. Разложение сигнала по ортонормированному базису обеспечивает минимум ошибки аппроксимации. 2. Ряд Котельникова представляет собой частный случай обобщенного ряда Фурье. Базисными функциями в этом случае являются функции отсчета, сдвинутые во времени относительно друг друга на интервалы, кратные 1/2fв. Коэффициентами ряда Котельникова служат отсчеты разлагаемого процесса, взятые через равные промежутки времени Dt=1/2fв. Если в спектре процесса отсутствуют составляющие с частотами выше fв, то ряд Котельникова дает точное в среднеквадратическом смысле представление процесса.
1.4.2. Квантование
После дискретизации реализации непрерывного процесса (сообщения) он может быть представлен совокупностью отсчетов, каждый из которых, вообще говоря, может иметь бесконечное множество значений. Реальные получатели сообщений имеют конечную разрешающую способность, т.е. весьма малый, но не нулевой интервал, внутри которого все разные значения отсчетов воспринимаются как одинаковые. Сказанное свидетельствует о целесообразности квантования. Квантование функции есть, по сути, отображение непрерывного множества ее возможных значений на конечное подмножество ее значений, каждое из которых представляется в виде одного из заранее определенных дискретных уровней, называемых уровнями квантования. Под шагом квантования понимается разность Dx = xm-xm-1 значений соседних уровней квантования. Число уровней квантования n на единицу больше числа интервалов квантования n-1. Если квантуемая функция x ограничена диапазоном от xmin до xmax, то n-1= (xmax- xmin)/ Dx. При квантовании обычно истинное значение функции x отождествляется или заменяется значением xi, соответствующим ближайшему уровню квантования. Естественно, замена истинных значений на значения уровней квантования приводит к ошибке e=xi-x, называемой ошибкой или шумом квантования. Обычно полагается, что при равномерном квантовании, когда Dx=const, шум квантования – случайная величина с равномерным законом распределения в пределах шага квантования. Максимальная ошибка квантования не превосходит половины шага квантования Dx / 2. Среднеквадратическая ошибка квантования равна корню квадратному из дисперсии равномерного распределения Таким образом, ошибка квантования уменьшается с уменьшением шага квантования Dx. Однако при уменьшении шага растет число уровней квантования, а, следовательно, растет и разрядность чисел, требуемая для их представления. Кроме того, при уменьшении шага квантования его величина может оказаться сопоставимой с уровнем помех. Так что к выбору величины шага квантования необходимо подходить с тех же позиций, что и к выбору шага дискретизации, т.е. выбирать оптимальный шаг квантования с точки зрения обеспечения минимума уровней квантования и заданной величины ошибки квантования. Рассмотренное квантование производилось с постоянным шагом Dx=const, вследствие чего квантованная функция состояла из одинаковых по величине ступенек. Некоторые функции, подлежащие квантованию, изменяются так, что их целесообразно квантовать с различным приращением уровней, т.е. с переменным шагом квантования Dx=var. Так, например, если необходимо получить более точные значения в какой-либо части квантуемой функции, то в этом диапазоне шаг квантования следует уменьшить. Таким образом, после выполнения операций дискретизации и квантования непрерывное сообщение представляется конечной последовательностью отсчетов, величина которых может принимать только вполне определенные значения, соответствующие уровням квантования. Если сопоставить каждому уровню квантования число, то непрерывное сообщение в результате выполнения операций дискретизации и квантования будет представлять собой последовательность чисел из конечного интервала, т.е. будет представлено в цифровой форме.
|

 Рис. 1.7
Рис. 1.7
 Рис. 1.8
Рис. 1.8
 Рис. 1.9
Рис. 1.9
 Рис. 1.10
Рис. 1.10
 .
. , образующие базис Котельникова, называют функциями отсчета. Они отличаются друг от друга только сдвигом по оси времени (рис. 1.11) на интервалы, кратные Dt.
, образующие базис Котельникова, называют функциями отсчета. Они отличаются друг от друга только сдвигом по оси времени (рис. 1.11) на интервалы, кратные Dt.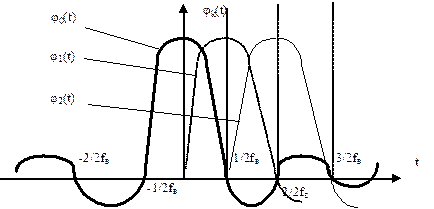
 , где X(kDt) - сечения процесса X(t), взятые через интервалы Dt, сходится в среднеквадратическом смысле к процессу X(t)».
, где X(kDt) - сечения процесса X(t), взятые через интервалы Dt, сходится в среднеквадратическом смысле к процессу X(t)».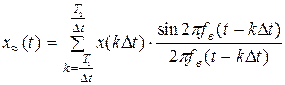 .
. , а относительное
, а относительное  , где знаменатель представляет собой полную мощность сигнала x(t), а числитель - часть его мощности, отброшенную при введении ограничения по времени и ограничения по спектру.
, где знаменатель представляет собой полную мощность сигнала x(t), а числитель - часть его мощности, отброшенную при введении ограничения по времени и ограничения по спектру. , где
, где  - значение коэффициента корреляции процесса X(t) при аргументе Dt. Из этой формулы при заданной погрешности dд можно получить выражение для допустимой величины шага дискретизации
- значение коэффициента корреляции процесса X(t) при аргументе Dt. Из этой формулы при заданной погрешности dд можно получить выражение для допустимой величины шага дискретизации  , где
, где  - функция, обратная коэффициенту корреляции процесса X(t).
- функция, обратная коэффициенту корреляции процесса X(t). или
или  .
. , т.е. в Ö3 раз меньше максимальной ошибки.
, т.е. в Ö3 раз меньше максимальной ошибки.


