КОЛИЧЕСТВЕННЫЕ ОЦЕНКИ ИНФОРМАЦИОННЫХ ОБЪЕКТОВ И ПРОЦЕССОВ
2.1. Подходы к определению количества информации
Одним из фундаментальных понятий теории информации является понятие количества информации. В связи с этим возникает вопрос об установлении меры количества информации. Существует множество различных подходов и, следовательно, различных мер количества информации. Основными из этих подходов являются структурный, статистический и семантический подходы. При структурном походе рассматривается строение и структура массивов информации и их измерение простым подсчетом максимально возможного количества информационных элементов, которое определяется этой структурой. Под информационными элементами понимаются неделимые частицы – кванты информации в дискретных моделях реальных информационных комплексов, а также элементы алфавитов в числовых системах. При структурном подходе различают геометрическую, комбинаторную и аддитивную меры информации. Геометрической мерой определяется потенциальное, т.е. максимально возможное количество информации в заданных структурных габаритах, называемое информационной емкостью информационной системы. Информационная емкость может быть представлена числом, показывающим, какое количество квантов содержится в массиве информации. К комбинаторной мере целесообразно прибегать тогда, когда требуется оценить возможность передачи информации при помощи различных комбинаций информационных элементов. Образование комбинаций есть одна из форм кодирования информации. Количество информации в комбинаторной мере вычисляется как количество комбинаций элементов. Таким образом, оценке подвергается комбинаторное свойство потенциального структурного разнообразия информационных систем. Комбинирование возможно в системах с неодинаковыми элементами, переменными связями или разнообразными позициями. Наибольшее распространение получила аддитивная мера, так называемая мера Хартли, измеряющая количество информации в двоичных единицах. Таким образом, структурный подход применяется для оценки потенциальных возможностей информационной системы вне зависимости от условий ее применения. При статистическом подходе учитывается вероятностный характер появления того или иного сообщения и устанавливается зависимость количества информации, содержащегося в сообщении, от вероятности появления этого сообщения. Таким образом, статистический подход учитывает конкретные условия применения информационных систем. С другой стороны, при статистическом подходе совершенно не учитывается смысловое содержание и субъективная ценность сообщения. Для оценки этих и других подобных характеристик используется семантический подход к установлению количественной меры информации. Семантический подход вводит меры содержательности, целесообразности и существенности информации. Оценка содержательности информации требует формализации смысла. За основу описания объекта берется атомарное, т.е неделимое предложение или квант сообщения. Мерой измерения смысла являются функции истинности и ложности логических высказываний. Эти функции имеют формальное сходство с функциями вероятности события и его отрицания в теории вероятностей. Отличие вероятностной оценки от логической состоит в том, что в первом случае учитывается вероятность реализации тех или иных событий, а во втором – меры истинности или ложности событий, что приближает их к оценке смысла информации. В качестве меры целесообразности информации предлагается использовать изменение вероятности достижения цели при получении информации. Полученная информация может не изменять вероятность достижения цели, и в этом случае мера ее целесообразности равна нулю, она может уменьшать вероятность достижения цели и тогда будет равна отрицательной величине, или увеличивать вероятность достижения цели и принимать положительное значение. Функция существенности отражает степень важности информации о том или ином значении параметра события с учетом времени и пространства. В настоящем курсе будет рассматриваться только статистический подход к установлению количественной меры информации. Это объясняется тем, что статистический подход так или иначе включает в себя структурный подход в качестве частного предельного случая, а основы семантического подхода являются предметом изучения в последующих дисциплинах учебного плана специальности.
2.2. Основы статистического подхода к определению количества информации
Интуитивно понятно, что количество информации, которое получает адресат, приняв сообщение, некоторым образом связано с априорной неопределенностью (доопытной, существовавшей до получения сообщения), которая, в свою очередь, зависит от числа возможных сообщений. Чем больше число возможных сообщений, тем больше априорная неопределенность получения одного из них и тем большее количество информации получает адресат, когда эта неопределенность снимается после получения сообщения. Первая попытка ввести научно обоснованную меру количества информации была сделана в 1928 году Р. Хартли. Он предложил и обосновал количественную меру, позволяющую сравнивать способность различных систем передавать информацию. Эта мера подходит как для систем передачи, так и для систем хранения информации, поэтому она явилась отправной точкой для создания теории информации. Естественным требованием, предъявляемым к информационной мере, является ее аддитивность: количество информации, которое можно сохранить в двух однотипных ячейках, должно быть в два раза больше, а в n одинаковых ячейках в n раз больше, чем в одной ячейке. Если ячейка для хранения информации имеет m возможных состояний, то две такие ячейки будут иметь m2 возможных состояний, а n одинаковых ячеек – mn возможных состояний. Следовательно, существует экспоненциальная зависимость между числом возможных состояний и числом ячеек. Учитывая эту зависимость, для количественной оценки способности системы хранить или передавать информацию Хартли ввел логарифмическую меру информационной емкости Ih=log m, (2.1) где m -число различных состояний системы. Такая мера удовлетворяет требованию аддитивности. Емкость устройства, состоящего из n ячеек и имеющего mn состояний, равна емкости одной ячейки, умноженной на число ячеек C= log mn=n log m. За единицу измерения информационной емкости принята двоичная единица – бит, равная емкости одной ячейки с двумя возможными состояниями. Хартли ограничился рассмотрением информационной емкости как величины характеризующей физическую систему. Эта оценка дает представление о потенциальной максимально возможной информационной емкости информационной системы, в ней не учтены вероятности различных состояний. Таким образом, мера Хартли, строго говоря, является не статистической, а структурной мерой количества информации. Дальнейшее развитие теория информации получила в трудах К.Шеннона, который ввел в нее понятия неопределенности и энтропии. Он ограничил применимость формулы Хартли (2.1) лишь тем случаем, когда все m исходов опыта X (т.е. состояний системы) равновероятны. В этом случае вероятность любого исхода
Принципиальное отличие этой формулы от (2.1.) состоит в том, что она показывает, что неопределенность исхода зависит от вероятности исхода. Далее Шеннон применил эту формулу к разновероятным событиям, усреднив затем полученные неопределенности по всем исходам. Для опыта X = {x1,... xm}, где x1,... xm - возможные исходы с вероятностями p1,... pm, неопределенность каждого исхода -logp1,... -logpm, а математическое ожидание по формуле
Получаемую по формуле (2.3) величину Шеннон назвал энтропией. Таким образом, неопределенность каждой ситуации характеризуется величиной, называемой энтропией. Понятие энтропии существует в ряде областей знаний. Энтропия в термодинамике означает вероятность теплового состояния вещества, в математике – степень неопределенности ситуации или задачи, в теории информации – способность источника отдавать информацию. Все эти понятия родственны между собой. Так, например, согласно второму закону термодинамики энтропия замкнутого пространства выражается как Поясним далее соотношение понятий энтропии и количества информации. В соответствии с определением понятия энтропия является мерой априорной неопределенности, существовавшей до получения сообщения. Под количеством информации, содержащимся в сообщении, понимается мера снятой неопределенности после получения сообщения. Предположим, что до получения сообщения ситуация характеризовалась энтропией H1, после получения сообщения энтропия уменьшилась и стала равной H2. Тогда количество информации, содержащееся в этом сообщении, равно I = H1 - H2. Если неопределенность в результате получения сообщения снимается полностью, т.е. H2 = 0, то I = H1 или I = Hаприорн. - Hапостериорн .. Энтропия обладает следующими свойствами: 1. Энтропия всегда неотрицательна, т.к. значения вероятностей выражаются числами, не превосходящими единицу, а их логарифмы, следовательно, отрицательными числами, так что члены суммы в формуле (2.3) всегда положительны. 2. Энтропия равна 0 в том и только в том случае, когда вероятность одного из исходов pk = 1, следовательно, вероятность всех остальных исходов равна 0. Это соответствует тому случаю, когда исход опыта может быть предсказан с полной достоверностью и отсутствует всякая неопределенность, сообщение об исходе не несет никакой информации. 3. Энтропия имеет наибольшее значение, когда вероятности всех исходов равны между собой p1 = p2... = pm = 1/m, тогда
Если полученное выражение сравнить с (2.1), то это явится еще одним доказательством того, что мера Хартли дает представление о потенциальных возможностях информационной системы. В случае неравенства вероятностей количество информации по Шеннону меньше информационной емкости системы. Рассмотрим простейший пример с элементарным двоичным событием. 1) пусть p1 = p2 = 0,5, тогда H = -(0,5log0,5 + 0,5log0,5) = 1 бит; 2) пусть p1 = 0,9, p2 = 0,1, тогда H = -(0,9log0,9 + 0,1log0,1) = 0,46 бит; 3) пусть p1 = 1, p2 = 0, тогда H = -(1log1 + 0log0) = 0 бит. Если во всех полученных выражениях под опытом X понимать способность некоторого дискретного источника формировать то или иное сообщение из их совокупности X, то все сказанное о количестве информации и энтропии может быть отнесено к источнику информации. Введение понятия энтропии источника позволяет дать точные определения упомянутых во введении характеристик, называемых избыточностью источника и производительностью источника. Относительная избыточность источника определяется по формуле
где m - объем алфавита источника, т.е. способность формировать m различных сообщений (символов). Относительная избыточность показывает, какая доля максимально возможной при данном объеме алфавита энтропии не используется источником. Пусть, например, источник выдает символы x1, x2, x3, x4 с вероятностями p(x1)=0,2, p(x2)=0,3, p(x3)=0,4, p(x4)=0,1. Найти количество информации в каждом из символов источника при их независимом выборе (источник без памяти). Требуется найти энтропию и избыточность данного источника. Количество информации в каждом из символов xi определяется по формуле (2.2)
Энтропия источника, выдающего эти символы, находится по формуле (2.3)
Избыточность источника зависит как от степени неравновероятности отдельных символов, так и от наличия и протяженности статистических связей между последовательно выбираемыми символами, т.е. от памяти источника. Если источник без памяти, т.е. последовательно передаваемые символы независимы, и все символы равновероятны, то H(X) = Hmax и rотн = 0. Источник, как и случайный процесс, называется стационарным, если описывающие его вероятностные характеристики не меняются во времени. Пусть, например, стационарный источник выдает за время Т=106 секунд 10 7 бит информации двоичными посылками длительностью t=10 мс. За какое время и каким количеством двоичных посылок можно передать тот же объем информации, если соответствующей обработкой полностью устранить избыточность источника. Определить избыточность источника. Заданное количество информации I = 107 бит источник передает n посылками или символами, где n = Т/t = 108. Тогда среднее количество информации, приходящееся на одну посылку или символ, H = I/n =0,1 бит/символ. Если в результате соответствующей обработки избыточность полностью устранена, то каждый символ двоичного источника несет в себе Hmax = 1 бит информации. Тогда заданное количество информации может быть передано n0= I/ Hmax = 107 посылками при той же их длительности t=10 мс за время T0 = t n0 =105 c. Избыточность источника по формуле (2.5) Если дискретный источник выдает сообщения, затрачивая в среднем время Т на каждое сообщение, то производительностью (в битах в секунду) такого источника называется суммарная энтропия сообщений, переданных в единицу времени
где
2.3. Энтропия объединения (ансамбля)
Формула (2.3) получена в предположении, что существует неопределенная ситуация X, которая характеризуется вполне определенным набором альтернатив x1, x2,..., xm и известными априорными вероятностями этих альтернатив p(x1), p(x2),..., p(xm). Таким образом, на множестве (ансамбле) возможных сообщений задается распределение вероятностей, и это позволяет вычислить по формуле (2.3) энтропию источника. Однако информационный акт в любой информационной системе состоит в передаче сообщения от источника к получателю. В связи с этим возникает необходимость в определении количества информации, содержащегося в одном ансамбле относительно другого. Для этого рассмотрим объединение двух дискретных ансамблей X и Y, вообще говоря, зависимых друг от друга. Интерпретировать это объединение в зависимости от решаемой задачи можно по-разному: а) как пару ансамблей сообщений, б) как ансамбль сообщений X и ансамбль сигналов Y, с помощью которого эти сообщения передаются, в) как ансамбль сообщений (сигналов) X на входе канала и ансамбль сообщений (сигналов) Y на выходе канала и т.д. При этом ансамбль Y задается аналогичной ансамблю X схемой
а схема объединения ансамблей выглядит следующим образом x1 x2... xm y1 p(x1y1) p(x2y1)... p(xmy1) y2 p(x1y2) p(x2y2)... p(xmy2) .... ym p(x1ym) p(x2ym)... p(xmym), где вероятности произведения совместных зависимых событий определяются по формуле С объединением событий связаны понятия совместной и условной энтропии и взаимной информации. Совместной энтропией H(XY) называется среднее количество информации на пару сообщений (например, переданного и принятого). По аналогии с теоремой умножения вероятностей (1.7)
Здесь Для условной энтропии справедливо неравенство Выражения для нахождения условных энтропий через вероятностные схемы ансамблей X и Y и их объединений могут быть получены исходя из следующего. Пусть на основании статистических данных могут быть установлены вероятности событий y1, y2,..., ym при условии, что имело место событие xi. Это будут условные вероятности p(y1/xi), p(y2/xi),..., p(ym/xi). Тогда частная условная энтропия будет равна по общему определению энтропии (2.3)
Далее нужно подсчитать среднее значение H(Y/X) для всех xi при i =1,..., n, т.е.
и аналогично
В общем случае условная энтропия H(X/Y) меньше H(X) и знание Y снижает в среднем априорную неопределенность X. Из этих соображений целесообразно назвать разность
количеством информации, содержащемся в Y относительно X. Эту величину называют взаимной информацией между X и Y. Взаимная информация измеряется в тех же единицах, что и энтропия, т.е. в битах. Величина I(X,Y) показывает, сколько в среднем бит информации получаем о реализации ансамбля X, наблюдая реализацию ансамбля Y. Основные свойства взаимной информации: 1. I(X, Y) ³0, причем равенство нулю имеет место тогда и только тогда, когда X и Y независимы друг от друга. (2.11) 2. I(X, Y) = I(Y, X), т.е. Y содержит такое же количество информации об X, какое X содержит относительно Y. (2.12) 3. I(X, Y) £ H(X), причем равенство имеет место тогда, когда по реализации Y можно однозначно восстановить X. (2.13) 4. I(Y, X) £ H(Y), причем равенство имеет место тогда, когда по реализации X можно однозначно восстановить реализацию Y. (2.14) 5. Полагая Y=X и учитывая, что H(X/X) = 0, получим, что I(X,X)=H(X). Это позволяет интерпретировать энтропию источника, как его собственную информацию, т.е. содержащуюся в ансамбле X о самом себе. (2.15) Все сказанное о безусловной, условной, совместной энтропии и взаимной информации можно свести в табл. 2.1. Таблица 2.1
Если обозначить T - среднее время передачи одного сообщения, а uк - количество символов, поступающих на вход канала в единицу времени, то величина
показывает количество информации, приходящееся не на одно сообщение, а на единицу времени и называется скоростью передачи информации от X к Y. Полученные соотношения позволяют взглянуть на сущность энтропии с другой точки зрения. Пусть X - ансамбль дискретных сообщений, а Y - ансамбль дискретных сигналов, в которые преобразуются сообщения X. Тогда (2.13, 2.14) I(X, Y) = H(X) в том и только в том случае, когда преобразование X ® Y обратимо. При необратимом преобразовании I(X, Y) < H(X) и разность H(X) - I(X,Y) = H(X/Y) можно назвать потерей информации при преобразовании X ® Y. Таким образом, информация не теряется только при строго обратимых преобразованиях. Далее, понимая под X ансамбль сигналов на входе дискретного канала, а под Y - ансамбль сигналов на его выходе, на основании (2.10) можно записать
Это соотношение можно проиллюстрировать рис. 2.1.
Рис. 2.1 Здесь H(X) - энтропия источника на входе канала, H(Y) - энтропия на выходе канала, H(X/Y) - потери информации в канале, эта величина называется иногда ненадежностью канала, H(Y/X) - посторонняя информация в канале, создаваемая действующими в нем помехами и называемая иногда энтропией шума. Соотношение между H(X/Y) и H(Y/X) определяется свойствами канала. Например, при передаче телефонного сигнала по каналу с узкой полосой частот и низким уровнем помех H(X/Y) >> H(Y/X). Если полоса частот канала достаточна, но сильны наводки от соседнего канала, то H(X/Y) << H(Y/X). Если в системе нет потерь информации, искажений и помех, то условные энтропии в выражении (2.17) равны нулю, а количество взаимной информации равно энтропии либо источника, либо приемника.
|

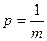 и тогда формулу Хартли (2.1.) можно переписать в следующем виде
и тогда формулу Хартли (2.1.) можно переписать в следующем виде . (2.2.)
. (2.2.)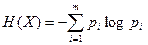 . (2.3.)
. (2.3.) , где N - общее количество молекул в данном пространстве, ni - количество молекул, имеющих скорость vi. Но
, где N - общее количество молекул в данном пространстве, ni - количество молекул, имеющих скорость vi. Но  есть частоты событий, следовательно, вероятности того, что молекулы имеют скорость vi,равна
есть частоты событий, следовательно, вероятности того, что молекулы имеют скорость vi,равна 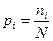 . Тогда
. Тогда  , что аналогично (2.3). Выбор основания логарифма несуществен, поскольку определяет лишь единицы измерения энтропии.
, что аналогично (2.3). Выбор основания логарифма несуществен, поскольку определяет лишь единицы измерения энтропии.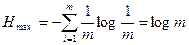 . (2.4.)
. (2.4.)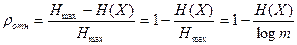 , (2.5)
, (2.5)
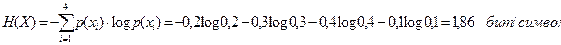 . Избыточность источника находится по формуле (2.5)
. Избыточность источника находится по формуле (2.5)  .
. .
. , (2.6)
, (2.6) - скорость источника, под которой понимается количество сообщений (символов), выдаваемых источником в единицу времени.
- скорость источника, под которой понимается количество сообщений (символов), выдаваемых источником в единицу времени. ,
,
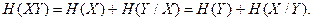 (2.7)
(2.7)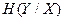 - условная энтропия Y относительно X или мера количества информации в приемнике, если известно, что передается X, а
- условная энтропия Y относительно X или мера количества информации в приемнике, если известно, что передается X, а  - условная энтропия X относительно Y или мера количества информации об источнике, когда известно, что принимается Y.
- условная энтропия X относительно Y или мера количества информации об источнике, когда известно, что принимается Y.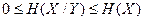 . При этом равенство
. При этом равенство 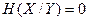 имеет место тогда, когда Y содержит полную информацию об X. Другое равенство
имеет место тогда, когда Y содержит полную информацию об X. Другое равенство  имеет место тогда, когда X и Y независимы, т.е. Y не содержит никакой информации об X.
имеет место тогда, когда X и Y независимы, т.е. Y не содержит никакой информации об X. .
.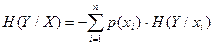 или в развернутом виде
или в развернутом виде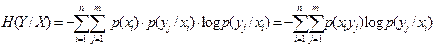 (2.8)
(2.8)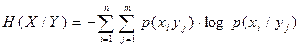 . (2.9)
. (2.9)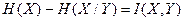 (2.10)
(2.10)





 (2.16)
(2.16)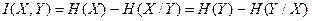 . (2.17)
. (2.17)



