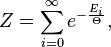Распределение по модулю скоростей
Обычно, более интересно распределение по абсолютному значению, а не по проекциям скоростей молекул. Модуль скорости, v определяется как:
поэтому модуль скорости всегда будет больше или равен нулю. Так как все
где
таким образом, функция плотности вероятности для модуля скорости равна
Распределение ферми дирака
Распределение (каноническое) Гиббса — распределение состояний макроскопической термодинамической системы частиц, находящейся в тепловом равновесии с термостатом (окружающей средой). В классическом случае плотность распределения равна
где
Часто используют следующую параметризацию распределения Гиббса:
где В квантовом случае предполагается счётное множество энергетических уровней, и вместо плотности распределения рассматривается вероятность нахождения системы в том или ином состоянии:
Условие нормировки имеет вид
что является аналогом интеграла состояний и называется суммой состояний или статистической суммой.
|

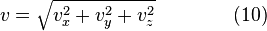
 распределены нормально, то
распределены нормально, то 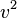 будет иметь хи-квадрат распределение с тремя степенями свободы. Если
будет иметь хи-квадрат распределение с тремя степенями свободы. Если 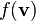 — функция плотности вероятности для модуля скорости, то:
— функция плотности вероятности для модуля скорости, то: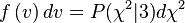 ,
,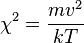


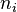 — среднее число частиц в состоянии
— среднее число частиц в состоянии 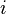 ,
,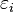 — энергия состояния
— энергия состояния  — кратность вырождения состояния
— кратность вырождения состояния 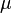 — химический потенциал (который равен энергии Ферми
— химический потенциал (который равен энергии Ферми 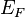 при абсолютном нуле температуры),
при абсолютном нуле температуры),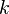 — постоянная Больцмана,
— постоянная Больцмана,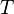 — абсолютная температура.
— абсолютная температура.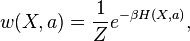
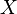 — совокупность
— совокупность 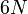 канонических переменных
канонических переменных 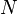 частиц (
частиц ( координат и
координат и  — совокупность внешних параметров,
— совокупность внешних параметров, 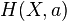 — гамильтониан (функция Гамильтона) системы,
— гамильтониан (функция Гамильтона) системы, 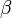 — параметр распределения. Величину
— параметр распределения. Величину 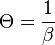 называют модулем распределения. Можно показать, что модуль распределения
называют модулем распределения. Можно показать, что модуль распределения 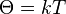 , где
, где  — параметр, определяемый исходя из условия нормировки
— параметр, определяемый исходя из условия нормировки 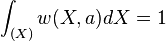 , откуда следует, что
, откуда следует, что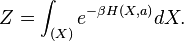
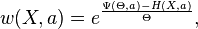
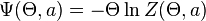 — так называемая свободная энергия системы.
— так называемая свободная энергия системы.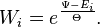
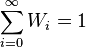 , следовательно
, следовательно