Распределение по вектору импульса
В случае идеального газа, состоящего из невзаимодействующих атомов в основном состоянии, вся энергия находится в форме кинетической энергии. Кинетическая энергия соотносится с импульсом частицы следующим образом
где Мы можем поэтому переписать уравнение (1) как:
где
Постоянная нормировки C, определяется из условия, в соответствии с которым вероятность того, что молекулы имеют какой-либо вообще импульс, должна быть равна единице. Поэтому интеграл уравнения (4) по всем значениям
Таким образом, чтобы интеграл в уравнении (4) имел значение 1 необходимо, чтобы
Подставляя выражение (6) в уравнение (4) и используя тот факт, что
|
,
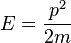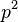— квадрат вектора импульса 
.
,
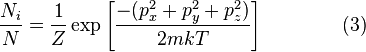— статсумма, соответствующая знаменателю в уравнении (1), 
— молекулярная масса газа,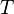 
— термодинамическая температура, и 
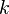—постоянная Больцмана. Это распределение 
пропорционально функции плотности вероятности 
нахождения молекулы в состоянии с этими значениями компонентов импульса. Таким образом:
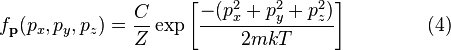
и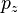 
должен быть равен единице. Можно показать, что:
.
.
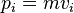, мы получим
.
