Энтропия. В курсе математики показано, чтобы дифференциальный двучлен превратить в полный дифференциал некоторой функцииВ курсе математики показано, чтобы дифференциальный двучлен превратить в полный дифференциал некоторой функции, необходимо умножить его на интегрирующий множитель (делитель). Для дифференциального уравнения I-го закона термодинамики δ q = Cv dT + p dV. Интегрирующим делителем является абсолютная температура, тогда
Выражение (11) является полным дифференциалом некоторой функции состояния рабочего тела dS, названной энтропией.
Энтропия S есть функция состояния рабочего тела. Отметим, что пари увеличении энтропии (dS > 0) тепло подводится к рабочему телу (δ q > 0). При уменьшении энтропии (dS < 0) тепло отводится (δ q < 0). В термодинамических расчетах пользуются величиной изменения энтропии. Вычислить изменение энтропии в термодинамическом процессе можно путем интегрирования выражения:
|
. 
, 
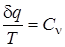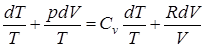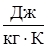. (11)
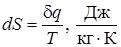. (12)
.
.
