Задача 1. Осевые опоры скольжения
Расчетно-графическая работа №2 Расчет опор и фрикционных соединений
Задача 1. Осевые опоры скольжения
Кроме того, предполагается, что интенсивность изнашивания каждого из сопрягаемых тел является линейной функцией давления, т. е. I = Kq. Кинетика изменения контактных давлений в сопряжении в процессе износа описывается дифференциальным уравнением
где
ki – коэффициент податливости упругого слоя, м×Па-1; Ki — коэффициент интенсивности изнашивания, Па-1; а и b — внутренний и наружный радиусы пяты, м; t — текущее время, с; q(r', t) — давление на контакте, Па; q (0) — давление в начальный момент времени; F2 (t) — функция, пропорциональная скорости сближения тел в процессе износа v(t), F2(t) = kSv (t); i = 1, 2 — индексы, относящиеся к пяте и подпятнику. Если полагать, что неровности имеют форму призм и сминаются упруго, то для коэффициента податливости, исходя из закона Гука для деформации растяжения сжатия, можно записать
где h0i – высота каждого из контактирующих элементов; F – фактическая площадь контакта двух поверхностей; ts – относительная опорная площадь. Тогда
Численный анализ (5.79) показал, что скорость изнашивания сопряжения может быть представлена в виде
где
Если t>>t*/l, то
Если t<<t*/l, то
Если известен предельный износ сопряжения h*, то учитывая, что t>>t*/l, из формулы (5.82) получим
Пример 1. Рассчитаем износ соединения пяты из Бр.ОЦС5—5—5 и стального подпятника из стали 20Х через 3 с работы. Осевая сила составляет P = 1000 Н. Е 1 = 9,45×1010 Па, Е 2 = 1,96×1011 Па. Внутренний диаметр пяты 2 а = 3×10-2 м, наружный диаметр пяты 2 b = 15×10-2 м. Высота пяты h01 = 5×10-2 м, подпятника h02 = 7,5×10-2 м. Значения коэффициента износа соответственно равны K 1 = 1,93×10-10, K 2 = 4×10-11 (табл. 5.6). Относительная опорная поверхность tS = 0,5. Рассчитаем также ресурс работы сопряжения, если предельный износ составляет h* = 2×10-2 м. Решение. По примечанию к формуле (5.79) определим суммарную высоту опоры, суммарный коэффициент податливости, суммарный коэффициент износа коэффициент b
По графику на рисунке 5.32 определяем, что l = 0,6. По примечанию к формуле (5.80) определим скорость изнашивания в начальный момент времени и устоявшуюся скорость изнашивания, а также характерной время
Поскольку t= 3 с » t*/l= 3,2 с, величину износа рассчитываем по формуле (5.81)
Если бы необходимо было определить износ опоры через 5 ч эксплуатации, то t = 18000 с >>; t*/l = 3,2 с, и по формуле (5.82)
Ресурс работы сопряжения
Варианты для расчета к задаче №1 даны в таблице 5.1.
|

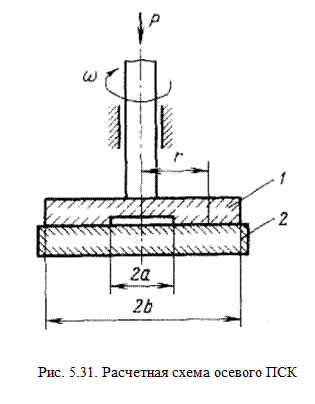 Расчетная схема осевого подшипника скольжения представлена на рис. 5.31. Он состоит из плоской кольцевой пяты 1, опирающейся на подпятник 2. Пята вращается с угловой скоростью w и нагружена осевой силой Р. Поскольку участки рабочих поверхностей пяты и подпятника, расположенные на разных расстояниях от оси вращения, изнашиваются с разной скоростью (у них разные пути трения), условие неразрывности контакта в процессе эксплуатации может быть выполнено лишь с учетом конечной жесткости контакта. В связи с этим рассмотрим задачу об износе такого сопряжения, считая, что пята и подпятник являются жесткими, а их контактные деформации w, обусловленные шероховатостью, пропорциональны давлению q, т. е. w = kq. При этом, несмотря на износ сопрягаемых тел, шероховатость поверхностей сохраняется, и в первом приближении деформационные свойства ее можно считать независящими от времени.
Расчетная схема осевого подшипника скольжения представлена на рис. 5.31. Он состоит из плоской кольцевой пяты 1, опирающейся на подпятник 2. Пята вращается с угловой скоростью w и нагружена осевой силой Р. Поскольку участки рабочих поверхностей пяты и подпятника, расположенные на разных расстояниях от оси вращения, изнашиваются с разной скоростью (у них разные пути трения), условие неразрывности контакта в процессе эксплуатации может быть выполнено лишь с учетом конечной жесткости контакта. В связи с этим рассмотрим задачу об износе такого сопряжения, считая, что пята и подпятник являются жесткими, а их контактные деформации w, обусловленные шероховатостью, пропорциональны давлению q, т. е. w = kq. При этом, несмотря на износ сопрягаемых тел, шероховатость поверхностей сохраняется, и в первом приближении деформационные свойства ее можно считать независящими от времени. , (5.79)
, (5.79) ,
,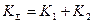 ,
,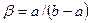 ,
, ,
, ,
,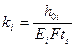 , (5.79 а)
, (5.79 а) . (5.79 б)
. (5.79 б) , (5.80)
, (5.80)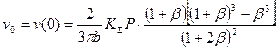 ;
;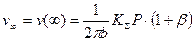 ;
; - характерное время;
- характерное время;











 l — параметр, зависящий от b (рис. 5.32).
l — параметр, зависящий от b (рис. 5.32).
 Износ сопряжения h за время t подсчитывается по формуле
Износ сопряжения h за время t подсчитывается по формуле . (5.81)
. (5.81) . (5.82)
. (5.82)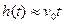 . (5.83)
. (5.83)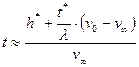 . (5.82а)
. (5.82а) м,
м, м×Па-1,
м×Па-1, Па-1,
Па-1, .
.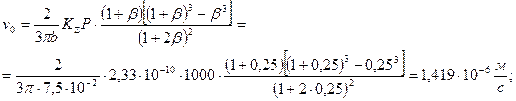
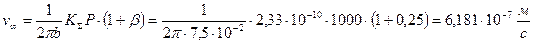 ;
;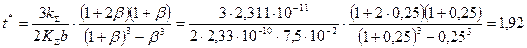 с.
с.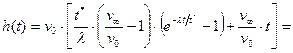
 м = 3,414 мкм.
м = 3,414 мкм. мм.
мм. с» 9 ч.
с» 9 ч.


