Задача 3. Расчет ресурса подшипника скольжения с учетом износа цапфы и втулки.
 Если значения износостойкости материалов цапфы и втулки не сильно разнятся, то предположение о неизнашиваемости одного из этих элементов является грубым. В этом случае износ сопряжения определяется износом как втулки, так и цапфы. Если значения износостойкости материалов цапфы и втулки не сильно разнятся, то предположение о неизнашиваемости одного из этих элементов является грубым. В этом случае износ сопряжения определяется износом как втулки, так и цапфы.
При расчете ресурса такого подшипника скольжения сделаем следующие дополнительные предположения: контактирующие тела считаются жесткими; интенсивность изнашивания каждого из сопрягаемых тел является линейной функцией давления.
Начальное состояние сопряжения в соответствии с первым допущением характеризуется нулевым углом контакта и соответственно бесконечно большими контактными давлениями. В дальнейшем по мере износа цапфы и втулки угол контакта сопряжения увеличивается, в связи с чем меняются контактные давления. Излагаемая далее методика учитывает кинетику изменения этих параметров в процессе эксплуатации.
Ресурс сопряжения определяется допустимым изменением первоначального зазора, которое складывается из износа цапфы и максимального износа втулки в середине дуги контакта.
Последовательность расчета.
1. Вычисляют параметр b1,2:
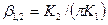 . (32) . (32)
2. Рассчитывают значения h* (10), y * (11) и h' = 1/ y*:
3. Используя табл. 9, по вычисленным значениям b1,2 и h' отыскивают предельный угол контакта j*0.
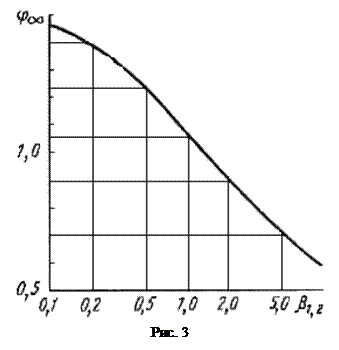
4. С помощью графика, приведенного на рис. 3, определяют значение угла j¥.
Таблица 9.
Значения предельного угла контакта j*0
| h'
| b1,2 = 0,2
| b1,2 = 0,4
| b1,2 = 0,6
| b1,2 = 0,8
| b1,2 = 1,0
| b1,2 = 2,0
| b1,2 = 3,0
| b1,2 = 4,0
| | 0,1
| 1,336
| 1,234
| 1,158
| 1,097
| 1,047
| 0,887
| 0,795
| 0,733
| | 0,2
| 1,276
| 1,185
| 1,115
| 1,060
| 1,014
| 0,864
| 0,776
| 0,716
| | 0,3
| 1,224
| 1,140
| 1,076
| 1,025
| 0,982
| 0,841
| 0,757
| 0,700
| | 0,4
| 1,177
| 1,100
| 1,041
| 0,933
| 0,953
| 0,819
| 0,739
| 0,684
| | 0,5
| 1,135
| 1,065
| 1,009
| 0,964
| 0,926
| 0,799
| 0,722
| 0,669
| | 1,0
| 0,979
| 0,926
| 0,884
| 0,849
| 0,819
| 0,716
| 0,652
| 0,607
| | 2,0
| 0,797
| 0,762
| 0,733
| 0,708
| 0,686
| 0,609
| 0,559
| 0,523
| | 4,0
| 0,617
| 0,596
| 0,577
| 0,561
| 0,547
| 0,493
| 0,457
| 0,431
| | 6,0
| 0,523
| 0,507
| 0,493
| 0,481
| 0,470
| 0,428
| 0,399
| 0,377
| | 8,0
| 0,461
| 0,449
| 0,438
| 0,428
| 0,419
| 0,385
| 0,360
| 0,341
| | 10,0
| 0,418
| 0,408
| 0,398
| 0,390
| 0,383
| 0,353
| 0,331
| 0,314
| 5. По найденным значениям j¥ и  рассчитывают условное значение предельного угла контакта: рассчитывают условное значение предельного угла контакта:
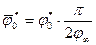 . (35) . (35)
6. Ресурс сопряжения рассчитывают по формуле
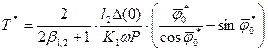 . (36) . (36)
Иногда необходимо оценить износ каждого элемента сопряжения в отдельности. Изложенная здесь постановка задачи позволяет это сделать. Сначала находят отношение износа цапфы к износу втулки:
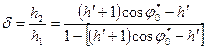 , (37) , (37)
а затем вычисляют отдельно износ цапфы
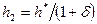 , (38) , (38)
и износ втулки
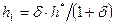 , (39) , (39)
Пример 3. Рассчитать ресурс подшипника скольжения при следующих исходных данных: R2 = 2,5×10-2 м, 12 = 5×10-2 м; Δ (0) = 5×10-5 М; Р = 5×103 Н; Δ* = 3,0×10-4 м; w = 1,57 с-1; К1 = 2,5×10-16 Па-1; К2 = 1,57×10-15 Па-1.
Из (32) получаем
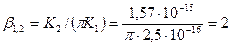 . .
Вычисляем значения h * по (10), y * по (11) и h’
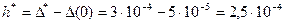 , ,
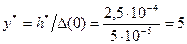 , ,
h' = 1/ y* = 1/5 = 0,2.
По таблице 9 для определенных ранее значений h' и b1,2 отыскиваем предельный угол контакта  = 0,863. = 0,863.
С помощью графика, приведенного на рис. 3, определяем j¥ = 0,912.
Вычисляем значение 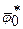 по (35): по (35):
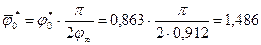 . .
В заключение рассчитываем ресурс сопряжения по (36):
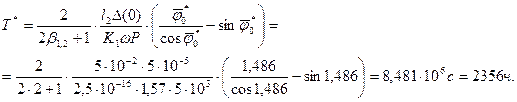
Износ каждого из элементов подвижного сопряжения в момент времени t = Т* рассчитывается по (38) и (39). Для данного примера
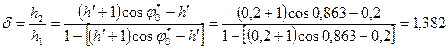 , ,
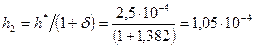 м, м,
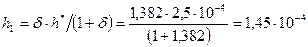 м. м.
Аналогично решаются и некоторые обратные задачи, когда по заданному ресурсу сопряжения требуется подобрать, например, геометрические размеры тел, нагрузку и т. п. Однако, если вопрос сводится к подбору материалов пары трения, то задача становится очень сложной: параметр b1,2, характеризующий относительную износостойкость элементов сопряжения, входит неявным образом в выражение в скобках, стоящее в правой части (36). Определенную помощь здесь оказывает графическое представление результатов расчетов, которое в силу своей наглядности существенно упрощает поиск решения задачи.
На рис. 4 приведена такая система графиков, построенная в координатах Tw, h' и d, h' где 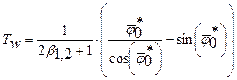 - параметр, зависящий от b1,2 и h’. - параметр, зависящий от b1,2 и h’.
Рассмотрим другую задачу. Требуется подобрать материал покрытия цапфы подшипника скольжения и толщину покрытия, если заданы характеристики сопряжения: l 2, Δ(0), K1, w, Р. Кроме того, известно, что долговечность подшипника должна быть не меньше 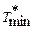 , а суммарный износ сопряжения при этом не должен быть больше , а суммарный износ сопряжения при этом не должен быть больше 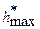 . В качестве материала покрытия могут быть использованы, скажем, три материала М1, М2, М3, характеризуемые соответственно коэффициентами интенсивности изнашивания . В качестве материала покрытия могут быть использованы, скажем, три материала М1, М2, М3, характеризуемые соответственно коэффициентами интенсивности изнашивания 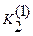 , , 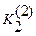 , , 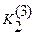 . .
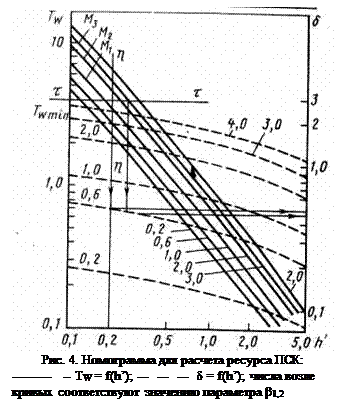 По исходным данным вычислим минимальное значение параметра По исходным данным вычислим минимальное значение параметра 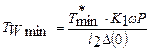 [см. формулу (36)]. Этому значению на рис. 5.30 соответствует прямая t - t. Через точку на оси абсцисс, соответствующую h* = h*max проведем прямую h — h. Условиям задачи будут удовлетворять лишь те кривые, отличающиеся по параметру b1,2 , которые проходят через часть плоскости, ограниченную снизу и слева прямыми t - t и h — h) соответственно. Пусть, например, для материала [см. формулу (36)]. Этому значению на рис. 5.30 соответствует прямая t - t. Через точку на оси абсцисс, соответствующую h* = h*max проведем прямую h — h. Условиям задачи будут удовлетворять лишь те кривые, отличающиеся по параметру b1,2 , которые проходят через часть плоскости, ограниченную снизу и слева прямыми t - t и h — h) соответственно. Пусть, например, для материала 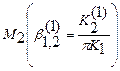 зависимость Tw от h' проходит вне этой части плоскости, а для материалов М2 и М3 — внутри нее. Следовательно, условиям задачи будут удовлетворять материалы М2 и М3. зависимость Tw от h' проходит вне этой части плоскости, а для материалов М2 и М3 — внутри нее. Следовательно, условиям задачи будут удовлетворять материалы М2 и М3.
Поскольку за ресурс сопряжения цапфа не должна износиться на величину, большую, чем толщина покрытия, то его минимальную толщину можно считать равной износу цапфы. Последний для двух материалов М1 и М2 может быть найден с помощью графиков, построенных в системе координат d, h', и последующих расчетов по (38) и (39). Максимальная толщина покрытия для данного материала получается при условии, что h* = h*max, а минимальная — при значении h*, соответствующем пересечению кривой Tw= f (h ') с прямой t - t.
Задания и варианты к выполнению расчетно-графической работы №1
Постоянные данные: h 0 = 10-3 м, D* = 5×10-4 м, f = 0,12, Е 1 = Е 2 = 1,96×1011 Па, Е 3 = 109 Па, m1 = m2 = 0,3, m2 = 0,4, l1 = 37 Вт/(м×К), a1 = 0,000013 K-1
Варианты выполнения работы.
| №
вар.
| R 2, м
| l 2, м
| D(0), м
| P, Н
| w, с-1
| l3,Вт/(м×К)
| a3, K-1
| K1
| m1
| K2
| m2
| | 1.
| 5×10-2
| 2,5×10-2
| 5×10-5
| 3×103
| 0,5
| 237 (Al)
| 0,004
| 2×10-19
|
| 4×10-18
|
| | 2.
| 5×10-2
| 2,5×10-2
| 5×10-5
| 3×103
|
| 91 (Cr)
| 0,003
| 10-19
| 1,2
| 10-18
| 1,5
| | 3.
| 5×10-2
| 2,5×10-2
| 5×10-5
| 6×103
| 0,5
| 69 (Co)
| 0,006
| 5×10-19
| 1,4
| 8×10-18
|
| | 4.
| 5×10-2
| 2,5×10-2
| 5×10-5
| 6×103
|
| 398 (Cu)
| 0,004
| 3×10-19
| 1,6
| 7×10-18
|
| | 5.
| 5×10-2
| 2,5×10-2
| 2,5×10-5
| 3×103
| 0,5
| 427 (Ag)
| 0,0038
| 2×10-19
| 1,8
| 4×10-18
| 1,5
| | 6.
| 5×10-2
| 2,5×10-2
| 2,5×10-5
| 3×103
|
| 315 (Au)
| 0,0035
| 10-19
|
| 10-18
|
| | 7.
| 5×10-2
| 2,5×10-2
| 2,5×10-5
| 6×103
| 0,5
| 67 (Sn)
| 0,00045
| 5×10-19
|
| 8×10-18
|
| | 8.
| 5×10-2
| 2,5×10-2
| 2,5×10-5
| 6×103
|
| 90,5 (Ni)
| 0,006
| 3×10-19
| 1,2
| 7×10-18
| 1,5
| | 9.
| 5×10-2
| 2×10-2
| 5×10-5
| 3×103
| 0,5
| 121 (Zn)
| 0,004
| 2×10-19
| 1,4
| 4×10-18
|
| | 10.
| 5×10-2
| 2×10-2
| 5×10-5
| 3×103
|
| 237 (Al)
| 0,004
| 10-19
| 1,6
| 10-18
|
| | 11.
| 5×10-2
| 2×10-2
| 5×10-5
| 6×103
| 0,5
| 91 (Cr)
| 0,003
| 5×10-19
| 1,8
| 8×10-18
| 1,5
| | 12.
| 5×10-2
| 2×10-2
| 5×10-5
| 6×103
|
| 69 (Co)
| 0,006
| 3×10-19
|
| 7×10-18
|
| | 13.
| 5×10-2
| 2×10-2
| 2,5×10-5
| 3×103
| 0,5
| 398 (Cu)
| 0,004
| 2×10-19
|
| 4×10-18
|
| | 14.
| 5×10-2
| 2×10-2
| 2,5×10-5
| 3×103
|
| 427 (Ag)
| 0,0038
| 10-19
| 1,2
| 10-18
| 1,5
| | 15.
| 5×10-2
| 2×10-2
| 2,5×10-5
| 6×103
| 0,5
| 315 (Au)
| 0,0035
| 5×10-19
| 1,4
| 8×10-18
|
| | 16.
| 5×10-2
| 2×10-2
| 2,5×10-5
| 6×103
|
| 67 (Sn)
| 0,00045
| 3×10-19
| 1,6
| 7×10-18
|
| | 17.
| 2,5×10-2
| 2,5×10-2
| 5×10-5
| 3×103
| 0,5
| 90,5 (Ni)
| 0,006
| 2×10-19
| 1,8
| 4×10-18
| 1,5
| | 18.
| 2,5×10-2
| 2,5×10-2
| 5×10-5
| 3×103
|
| 121 (Zn)
| 0,004
| 10-19
|
| 10-18
|
| | 19.
| 2,5×10-2
| 2,5×10-2
| 5×10-5
| 6×103
| 0,5
| 237 (Al)
| 0,004
| 5×10-19
|
| 8×10-18
|
| | 20.
| 2,5×10-2
| 2,5×10-2
| 5×10-5
| 6×103
|
| 91 (Cr)
| 0,003
| 3×10-19
| 1,2
| 7×10-18
| 1,5
| | 21.
| 2,5×10-2
| 2,5×10-2
| 2,5×10-5
| 3×103
| 0,5
| 69 (Co)
| 0,006
| 2×10-19
| 1,4
| 4×10-18
|
| | 22.
| 2,5×10-2
| 2,5×10-2
| 2,5×10-5
| 3×103
|
| 398 (Cu)
| 0,004
| 10-19
| 1,6
| 10-18
|
| | 23.
| 2,5×10-2
| 2,5×10-2
| 2,5×10-5
| 6×103
| 0,5
| 427 (Ag)
| 0,0038
| 5×10-19
| 1,8
| 8×10-18
| 1,5
| | 24.
| 2,5×10-2
| 2,5×10-2
| 2,5×10-5
| 6×103
|
| 315 (Au)
| 0,0035
| 3×10-19
|
| 7×10-18
|
| | 25.
| 2,5×10-2
| 2×10-2
| 5×10-5
| 3×103
| 0,5
| 67 (Sn)
| 0,00045
| 2×10-19
|
| 4×10-18
|
| | 26.
| 2,5×10-2
| 2×10-2
| 5×10-5
| 3×103
|
| 90,5 (Ni)
| 0,006
| 10-19
| 1,2
| 10-18
| 1,5
| | 27.
| 2,5×10-2
| 2×10-2
| 5×10-5
| 6×103
| 0,5
| 121 (Zn)
| 0,004
| 5×10-19
| 1,4
| 8×10-18
|
| | 28.
| 2,5×10-2
| 2×10-2
| 5×10-5
| 6×103
|
| 237 (Al)
| 0,004
| 3×10-19
| 1,6
| 7×10-18
|
| | 29.
| 2,5×10-2
| 2×10-2
| 2,5×10-5
| 3×103
| 0,5
| 91 (Cr)
| 0,003
| 2×10-19
| 1,8
| 4×10-18
| 1,5
| | 30.
| 2,5×10-2
| 2×10-2
| 2,5×10-5
| 3×103
|
| 69 (Co)
| 0,006
| 10-19
|
| 10-18
|
| | 31.
| 2,5×10-2
| 2×10-2
| 2,5×10-5
| 6×103
| 0,5
| 398 (Cu)
| 0,004
| 5×10-19
|
| 8×10-18
|
| | 32.
| 2,5×10-2
| 2×10-2
| 2,5×10-5
| 6×103
|
| 427 (Ag)
| 0,0038
| 3×10-19
| 1,2
| 7×10-18
| 1,5
|
[VeC1]Степень -10

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Билиодигестивные анастомозы Показания для наложения билиодигестивных анастомозов:
1. нарушения проходимости терминального отдела холедоха при доброкачественной патологии (стенозы и стриктуры холедоха)
2. опухоли большого дуоденального сосочка...
Сосудистый шов (ручной Карреля, механический шов). Операции при ранениях крупных сосудов 1912 г., Каррель – впервые предложил методику сосудистого шва.
Сосудистый шов применяется для восстановления магистрального кровотока при лечении...
Трамадол (Маброн, Плазадол, Трамал, Трамалин) Групповая принадлежность
· Наркотический анальгетик со смешанным механизмом действия, агонист опиоидных рецепторов...
|
Интуитивное мышление Мышление — это психический процесс, обеспечивающий познание сущности предметов и явлений и самого субъекта...
Объект, субъект, предмет, цели и задачи управления персоналом Социальная система организации делится на две основные подсистемы: управляющую и управляемую...
Законы Генри, Дальтона, Сеченова. Применение этих законов при лечении кессонной болезни, лечении в барокамере и исследовании электролитного состава крови Закон Генри:
Количество газа, растворенного при данной температуре в определенном объеме жидкости, при равновесии прямо пропорциональны давлению газа...
|
|

 Если значения износостойкости материалов цапфы и втулки не сильно разнятся, то предположение о неизнашиваемости одного из этих элементов является грубым. В этом случае износ сопряжения определяется износом как втулки, так и цапфы.
Если значения износостойкости материалов цапфы и втулки не сильно разнятся, то предположение о неизнашиваемости одного из этих элементов является грубым. В этом случае износ сопряжения определяется износом как втулки, так и цапфы.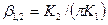 . (32)
. (32) рассчитывают условное значение предельного угла контакта:
рассчитывают условное значение предельного угла контакта: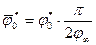 . (35)
. (35)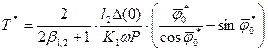 . (36)
. (36)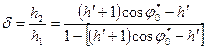 , (37)
, (37)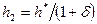 , (38)
, (38)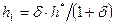 , (39)
, (39)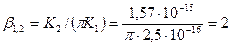 .
.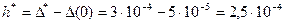 ,
,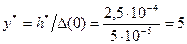 ,
,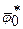 по (35):
по (35):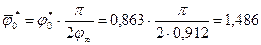 .
.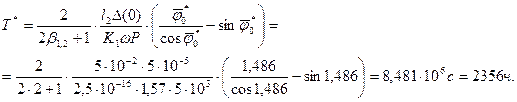
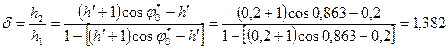 ,
,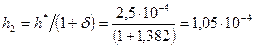 м,
м,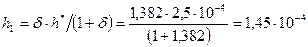 м.
м.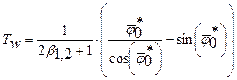 - параметр, зависящий от b1,2 и h’.
- параметр, зависящий от b1,2 и h’.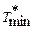 , а суммарный износ сопряжения при этом не должен быть больше
, а суммарный износ сопряжения при этом не должен быть больше 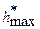 . В качестве материала покрытия могут быть использованы, скажем, три материала М1, М2, М3, характеризуемые соответственно коэффициентами интенсивности изнашивания
. В качестве материала покрытия могут быть использованы, скажем, три материала М1, М2, М3, характеризуемые соответственно коэффициентами интенсивности изнашивания 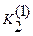 ,
, 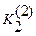 ,
, 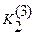 .
. По исходным данным вычислим минимальное значение параметра
По исходным данным вычислим минимальное значение параметра 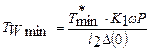 [см. формулу (36)]. Этому значению на рис. 5.30 соответствует прямая t - t. Через точку на оси абсцисс, соответствующую h* = h*max проведем прямую h — h. Условиям задачи будут удовлетворять лишь те кривые, отличающиеся по параметру b1,2 , которые проходят через часть плоскости, ограниченную снизу и слева прямыми t - t и h — h) соответственно. Пусть, например, для материала
[см. формулу (36)]. Этому значению на рис. 5.30 соответствует прямая t - t. Через точку на оси абсцисс, соответствующую h* = h*max проведем прямую h — h. Условиям задачи будут удовлетворять лишь те кривые, отличающиеся по параметру b1,2 , которые проходят через часть плоскости, ограниченную снизу и слева прямыми t - t и h — h) соответственно. Пусть, например, для материала 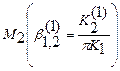 зависимость Tw от h' проходит вне этой части плоскости, а для материалов М2 и М3 — внутри нее. Следовательно, условиям задачи будут удовлетворять материалы М2 и М3.
зависимость Tw от h' проходит вне этой части плоскости, а для материалов М2 и М3 — внутри нее. Следовательно, условиям задачи будут удовлетворять материалы М2 и М3.


