Задача 2. Расчет подшипника скольжения с прямой парой трения.
При расчете такого ПСК делаются следующие дополнительные допущения. Цапфа в процессе эксплуатации не изнашивается, т. е. ресурс сопряжения полностью определяется износом АЭ (идеальная прямая пара). Цапфа и обойма втулки считаются недеформируемыми телами, а деформации локализованы в АЭ. Толщина АЭ мала по сравнению с размерами соприкасающихся тел, т. е. h0 /R2 << 1. Первое допущение выполняется тем точнее, чем больше отношение коэффициентов интенсивности изнашивания АЭ и цапфы. Можно руководствоваться такой оценкой, если K1/K2 > > 5, то с погрешностью, не превышающей 10%, допустимо считать цапфу неизнашиваемым элементом. Второе и третье допущения основаны на сложившейся практике конструирования опор скольжения, которая состоит в том, что модули упругости цапфы и обоймы на два-три порядка превосходят модуль упругости АЭ, а последний выполняется в виде тонкостенной втулки или тонкослойного покрытия. Следствием этих допущений является то, что АЭ ведет себя подобно телу Винклера, т. е. его осадка пропорциональна давлению. В методе расчета учитывается кинетика изменения контактных параметров сопряжения в процессе его эксплуатации и эволюция формы рабочей поверхности АЭ, обусловленная его изнашиванием. В связи с этим выделены две стадии процесса — начальная стадия (нестационарный режим), в течение которой изменение контактных параметров носит ярко выраженный нелинейный характер, и установившийся режим, когда на площадке контакта устанавливается распределение давления, близкое к косинусоидальному, а скорость изнашивания почти не меняется во времени. Последовательность расчета. 1. Вычисляют безразмерную нагрузку и толщину АЭ по формулам
где
Если при этом оказывается, что 1 < h'o < 100 и 0,5×10-3 < Р' < 4×10-3, то максимальный износ за время нестационарного режима составляет не более 0,1 начальной толщины АЭ. Учитывая, что скорость изнашивания в нестационарном режиме больше, чем в установившемся режиме, для соотношения продолжительности нестационарного режима изнашивания Т и ресурса Т* эта оценка заведомо справедлива. Если по условию задачи можно пренебречь нестационарным режимом изнашивания, то переходят сразу к п. 4 и в дальнейшем считают 2. С помощью табл. 6 и 7 находят значения вспомогательных Таблица 6. Значенияфункции N (P', h 'о)
Таблица 7. Значения функции М (в числителе) и L (в знаменателе)
3. Определяют угол контакта сопряжения в момент окончания не
и безразмерную продолжительность нестационарного режима
по которой затем рассчитывают реальное время нестационарного режима
4. Определяют предельное значение угла контакта в сопряжении, соответствующее предельно допустимому смещению оси вала относительно оси
5. Вычисляют продолжительность установившегося режима изнашивания, в конце которого радиальный зазор в сопряжении станет равным Δ*:
Значения функции F1 (m1,j0) приведены в табл. 8. 6. Определяют ресурс сопряжения: Т* = Частный случай. Если т1 = 1 и продолжительность нестационарного режима изнашивания составляет малую долю от ресурса подшипника (в случае 1 < h'o < 100 b; 0,5×10-8 < Р' < 4×10-3, T/T* ³ 0,95), ресурс рассчитывают по формуле
Пример 2. Определить ресурс подшипника скольжения при следующих значениях исходных параметров: R2 = 10-2м; l 2 = 2×10-2м; Δ(0) = 10-4м; h0 = 10-3 м; Р = 4×103 Н; Δ* = 5×10-4 м; w = 3,14 с-1; К1 = 3,82×10-18 Па-1.4; m1 = 1,4; Е3 = 109 Па; mз = 0,4.
Таблица 8. Значения функции F1(m1, j0)
Определим безразмерные параметры Р' и h'0 по (21) и (23)
Поскольку предельный износ подшипника h* = Δ* — Δ (0) составляет 4×10-4 м и отношение его к первоначальной толщине АЭ равно 0,25 и, кроме того, параметр Р не удовлетворяет условию, оговоренному в п. 1, то доля нестационарного режима изнашивания в общем ресурсе сопряжения уже значительна и ее следует учесть при расчетах. Определим значения вспомогательных функций N, М и L, пользуясь табл. 6 и 7. Поскольку в них отсутствует строка h'0 = 10 и столбец Р1’ = 9,34×10-3, то предстоит вычислить значения этих функций. Хороший результат дает метод параболической интерполяции по трем узлам. Выбирая в качестве узлов интерполяции Р1’ = 5×10-3; Р2’ = 7×10-3; Р3’ = 9×10-3 и h'0 = 1; h'0,2 = 2 1 и h'0,3 = 41, вычислим, например, сначала значения этих функций в точках (интерполяция по Р'), а затем (интерполяция по h'o) значение этих функций в точке (9,34×10-3; 10). В итоге получим N (9,34×10-3; 10) = 1,0641, М (9,34×10-3; 10) = 0,4762, L (9,34×10-3; 10) = -0,4326. Определим угол контакта в сопряжении в момент окончания нестационарного режима изнашивания по (25)
и безразмерную продолжительность нестационарного режима по (26)
Тогда реальное время нестационарного режима по (27)
Вычислим предельное значение угла контакта по (28)
С помощью табл. 5.13 определим значения функции F1 (m1, j0) при F1 (1,4, 61°) = 1,53, F2 (1,4, 78°46’) = 7,41.
а затем по (29) вычислим продолжительность стационарного режима изнашивания:
В заключение вычислим ресурс подшипника скольжения по (30):
|

 Расчетная модель. Традиционной конструктивной схемой ПСК является прямая пара трения, в которой роль АЭ выполняет втулка подшипника скольжения (рис. 2).
Расчетная модель. Традиционной конструктивной схемой ПСК является прямая пара трения, в которой роль АЭ выполняет втулка подшипника скольжения (рис. 2).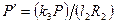 , (22)
, (22)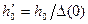 , (23)
, (23)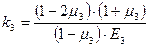 . (24)
. (24)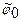 = 0,
= 0, 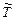 = 0. В противном случае переходят к следующему пункту методики расчета.
= 0. В противном случае переходят к следующему пункту методики расчета. (25)
(25)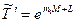 , (26)
, (26)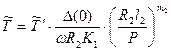 . (27)
. (27)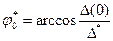 . (28)
. (28)
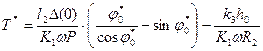 . (31)
. (31)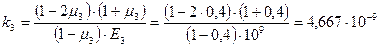 [VeC1] Па-1,
[VeC1] Па-1, ,
, .
.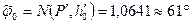
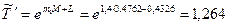 с.
с.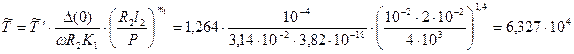 с.
с.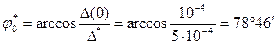 .
.

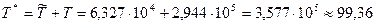 ч.
ч.


