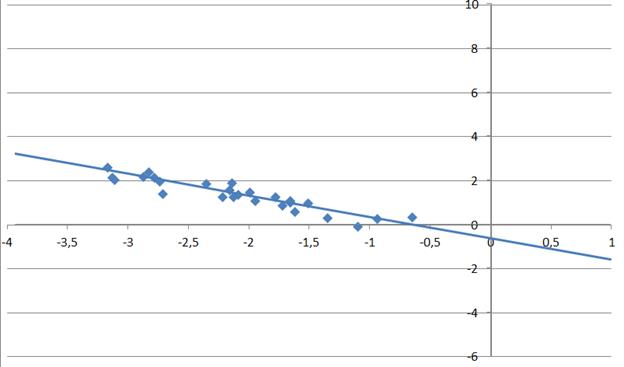
Двумерная выборка
Задание № 11
Исходные данные (столбцы xи y):
x
y
x2
y2
x*y
-1,1
-0,07
1,21
0,0049
0,077
-1,66
1,02
2,7556
1,0404
-1,6932
-2,35
1,88
5,5225
3,5344
-4,418
-2,87
2,17
8,2369
4,7089
-6,2279
-3,17
2,6
10,0489
6,76
-8,242
-2,13
1,26
4,5369
1,5876
-2,6838
-0,65
0,35
0,4225
0,1225
-0,2275
-1,72
0,87
2,9584
0,7569
-1,4964
-2,16
1,6
4,6656
2,56
-3,456
-2,83
2,38
8,0089
5,6644
-6,7354
-1,66
1,08
2,7556
1,1664
-1,7928
-3,13
2,16
9,7969
4,6656
-6,7608
-1,51
0,97
2,2801
0,9409
-1,4647
-1,95
1,09
3,8025
1,1881
-2,1255
-2,22
1,26
4,9284
1,5876
-2,7972
-3,11
2,06
9,6721
4,2436
-6,4066
-1,35
0,3
1,8225
0,09
-0,405
-2,71
1,42
7,3441
2,0164
-3,8482
-2,74
1,98
7,5076
3,9204
-5,4252
-2,14
1,91
4,5796
3,6481
-4,0874
-1,62
0,59
2,6244
0,3481
-0,9558
-1,78
1,27
3,1684
1,6129
-2,2606
-1,99
1,47
3,9601
2,1609
-2,9253
-0,94
0,27
0,8836
0,0729
-0,2538
-2,78
2,15
7,7284
4,6225
-5,977
среднее
-2,0908
1,3616
4,84882
2,360976
-3,30356
Количество двумерных чисел – 25.
В таблице получены:
- оценки математических ожиданий
mX =-2.0908
mY =1.3616
- оценки начальных моментов второго порядка по каждой переменной
- оценка смешанного начального момента второго порядка
На основе этих данных вычислим оценки дисперсий:
Оценка корреляционного момента равна:
XY =-0,47576
Точечная оценка коэффициента корреляции равна:
XY =-0,92836
Вычислим интервальную оценку коэффициента корреляции с надежностью g=0.95 по формуле:
zg- значение аргумента функции Лапласа, т.е. Ф(zg)=g/2=0.95/2=0.475, которое в нашем случае равно 1.96. Тогда коэффициенты a и b равны:
a=-2,06427
b=-1,22852
Таким образом, доверительный интервал для коэффициента корреляции имеет вид:
I(RXY )= [-0,9683; -0,84215]
Проверим гипотезу об отсутствии корреляционной зависимости:
Так как объём выборки невелик (n<50), то определяем значение критерия по следующей формуле:
t=11,9788
Из таблицы Стьюдента выбираем критическое значение tγ, n-2 , с учётом γ=1-α=0,95.
Значение tγ, n-2 =2,06. Так как t> tγ, n-2 , то гипотеза H0 отклоняется, т.е. величины X и Y коррелированы.
Вычисляем оценки параметров а0и а1линии регрессии
1 =-0,95675
0 =-0,63878
Уравнение линии регрессии примет вид:
<== предыдущая лекция | следующая лекция ==>
Отложение судебного разбирательства дела 2 страница | Програма курсу
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
Факторы, влияющие на степень электролитической диссоциации Степень диссоциации зависит от природы электролита и растворителя, концентрации раствора, температуры, присутствия одноименного иона и других факторов...
Йодометрия. Характеристика метода Метод йодометрии основан на ОВ-реакциях, связанных с превращением I2 в ионы I- и обратно...
Броматометрия и бромометрия Броматометрический метод основан на окислении восстановителей броматом калия в кислой среде...
Весы настольные циферблатные Весы настольные циферблатные РН-10Ц13 (рис.3.1) выпускаются с наибольшими пределами взвешивания 2...
Хронометражно-табличная методика определения суточного расхода энергии студента Цель: познакомиться с хронометражно-табличным методом определения суточного расхода энергии...
ОЧАГОВЫЕ ТЕНИ В ЛЕГКОМ Очаговыми легочными инфильтратами проявляют себя различные по этиологии заболевания, в основе которых лежит бронхо-нодулярный процесс, который при рентгенологическом исследовании дает очагового характера тень, размерами не более 1 см в диаметре...
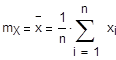
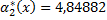
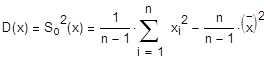D(x)=0,497266
D(y)=0,528147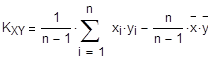
KXY=-0,47576
RXY=-0,92836
:
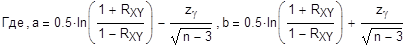
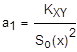a1=-0,95675
a0=-0,63878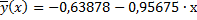
. Построим диаграмму рассеивания и линию регрессии:
