Дуополия Хотеллинга
Простая модель, предложенная в 1929 г. Г. Хотеллингом, в качестве одного из допущений использует пространственную дифференциацию продукта. Предполагается, что покупателями являются жители города, расположенного вдоль прямой (например, вдоль шоссейной или железной дороги). Длина города равна H, и он заселен равномерно. Две фирмы располагаются на противоположных концах города. Единственное различие производимого ими продукта состоит в том, что он продается в разных местах. Спрос — абсолютно неэластичный: в единицу времени жители желают приобрести a единиц товара на единицу длины вне зависимости от цены. Доставка товара требует от покупателя затрат в размере t за единицу товара на единицу расстояния. Покупатель, находящийся на расстояниях x 1 и x 2 от фирм, сравнивает свои расходы на покупку и доставку единицы товара от каждой из фирм (p 1 + tx 1 и p 2 + tx 2) и выбирает ту из фирм, чей товар обходится ему дешевле. Таким образом, город разбивается на две зоны, каждая из которых примыкает к «своей» фирме. Граница между зонами располагается на таких расстояниях x 1 и x 2 от фирм, где горожанам безразлично, у какой фирмы производить свои покупки. Положение границы определяется уравнениями p 1 + tx 1 = p 2 + tx 2; x 1 + x 2 = H, откуда x 1 = что позволяет записать функции спроса на продукцию фирм следующим образом: D 1(p 1, p 2) = Приведенные выражения справедливы, если более высокая цена превышает более низкую меньше, чем на величину tH — стоимость транспортировки единицы товара через весь город: при большей разнице цен фирма, назначившая высокую цену, не сможет продать ничего. Будем считать, что | p 1 – p 2| < tH. Выражения для спроса позволяют представить прибыль каждой фирмы в виде функции от обеих цен: P1(p 1, p 2) = P2(p 1, p 2) = Так как прибыль описывается непрерывно дифференцируемыми вогнутыми функциями, равновесие Нэша удовлетворяет дифференциальным условиям (¶P i / ¶ xi = 0, i =1, 2, …, N), которые применительно к рассматриваемой задаче принимают конкретный вид:
Разрешая первое из уравнений относительно p 1, второе — относительно p 2, получаем в явном виде функции реагирования фирм:
Совместное решение уравнений, порождаемых функциями реагирования, определяет равновесные цены:
В частном случае, когда затраты фирм одинаковы, p 1 = p 2 = c + tH. Приведенные результаты показывают, что пространственная дифференциация продукта создает условия для осуществления рыночной власти фирм, причем власть фирм оказывается тем сильнее, чем больше затраты на перевозку tH. И километровый тариф t, и взаимное удаление H мест продажи служат предпосылками рыночной власти фирм. Все выкладки, приведшие к результату (30), сделаны в предположении существования внутреннего равновесия Нэша. Но в дуополии Хотеллинга, как и в олигополии Курно, могут также существовать граничные положения равновесия, означающие несовместимость фирм в пределах одного рынка. Легко убедиться, что при | c 1 – c 2|³ 3 tH равенства (30) привели бы к таким ценам, при которых | p 1 – p 2|³ ³ tH, а ранее было оговорено, что в такой ситуации фирма с более дешевым товаром захватывает весь городской рынок. Пример с линейным городом служит иллюстрацией эффекта дифференциации продукта. Он служит метафорой дифференциации продукта в пространстве потребительских свойств товаров, где выбор потребителем той или иной разновидности определяется и соотношением цен, и степенью отличия свойств предлагаемых разновидностей от идеала данного потребителя.
|

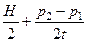 ; x 2 =
; x 2 = 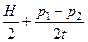 ,
,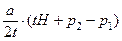 ; D 2(p 1, p 2) =
; D 2(p 1, p 2) = 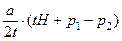 .
.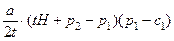 ;
;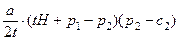 .
.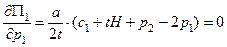 ;
;  .
. ;
; 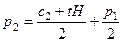 .
.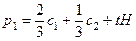 ;
; 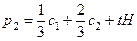 . (30)
. (30)



