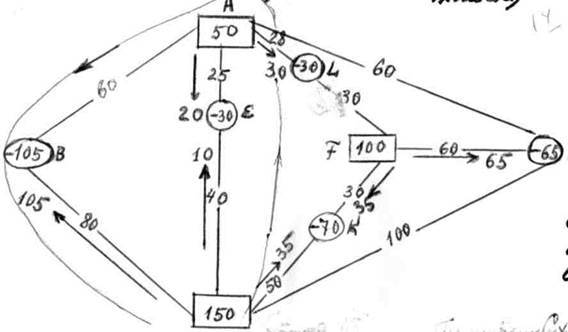
Схема 2. В результате улучшения (перераспределения) плана затраты на перевозку уменьшились на (+ 50 – 30 + 60 – 100) х 45 = - 900
В результате улучшения (перераспределения) плана затраты на перевозку уменьшились на (+ 50 – 30 + 60 – 100) х 45 = - 900 Исходя из первого условия критерия оптимальности, а именно: аjs – аis = Сs для хs > 0 определяем систему оценочных чисел. Пусть аA = 100 (задаём произвольно), тогда aE = 100 + 25 = 125 aL = 100 + 28 = 128 aF = 128 – 30 = 98 aD = 98 + 60 = 158 aK = 98 + 30 = 128 aC = 128 – 50 = 78 aB = 78 + 80 = 158. Проверим выполнение второго условия критерия оптимальности, а именно аjs - аis ≤ Сs для участков, на которых не осуществляется перевозка. aB – аA = 158 – 100 = 58 < 60 aD – аA = 158 – 100 = 58 < 60 aD – аC = 158 – 78 = 80 < 100 aE – аC = 125 – 78 = 47 > 40 - нарушение! Из проверки видно, что на участке СE не выполнено первое условие критерия оптимальности (47 > 40). Следовательно, по участку СЕ нужно осуществить перевозку. Строим кольцо (см. схему 2) и путём перераспределения вводим перевозку по участку СЕ. Получаем новый план (схема 3). ∆Э 3-2 = [(90 + 28 + 30) – (25 + 30 + 50)] … х 10... = - 70 ед.? Дальнейший процесс решения идентичен рассмотренному выше (составление системы оценочных чисел, проверка критерия оптимальности, введение перевозки на участке, где не выполнен критерий оптимальности).
|