1. Вычислить скалярное произведение двух векторов 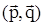 , зная их разложение по трем единичным взаимно перпендикулярным векторам
, зная их разложение по трем единичным взаимно перпендикулярным векторам 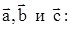
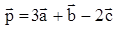 ;
; 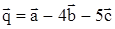 .
.
2. Найти длину вектора 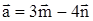 , зная, что
, зная, что  – взаимно перпендику-
– взаимно перпендику-
лярные орты.
3. Векторы  попарно образуют друг с другом углы, каждый из которых равен
попарно образуют друг с другом углы, каждый из которых равен  . Зная, что
. Зная, что 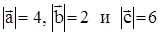 , определить модуль вектора
, определить модуль вектора  .
.
4. Доказать, что вектор  перпендикулярен к вектору
перпендикулярен к вектору 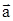 .
.
5. Даны векторы 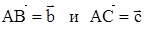 , совпадающие со сторонами треугольника АВС. Найти разложение вектора, приложенного к вершине В этого треугольника и совпадающего с его высотой BD по базису
, совпадающие со сторонами треугольника АВС. Найти разложение вектора, приложенного к вершине В этого треугольника и совпадающего с его высотой BD по базису 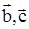 .
.
6. Вычислить угол между векторами 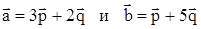 , где
, где 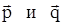 - единичные взаимно перпендикулярные векторы.
- единичные взаимно перпендикулярные векторы.
7. Даны силы 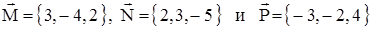 , приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения
, приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения  в положение
в положение 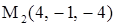 .
.
8. Даны вершины треугольника 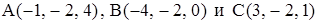 . Определить его внутренний угол при вершине В.
. Определить его внутренний угол при вершине В.
9. Вычислив внутренние углы треугольника с вершинами 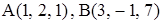 ,
, 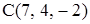 , убедиться, что этот треугольник равнобедренный.
, убедиться, что этот треугольник равнобедренный.
10. Найти вектор  , зная, что он перпендикулярен векторам
, зная, что он перпендикулярен векторам 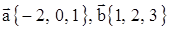 и
и  .
.
11. Найти вектор  , коллинеарный вектору
, коллинеарный вектору 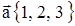 и удовлетворяющий условию
и удовлетворяющий условию  , где
, где 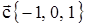 .
.
12. Вычислить проекцию вектора  на ось вектора
на ось вектора 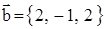 .
.
13. Даны векторы 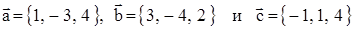 . Вычислить
. Вычислить 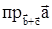 .
.
14. Даны точки 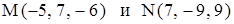 . Вычислить проекцию вектора
. Вычислить проекцию вектора  на ось вектора
на ось вектора 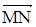 .
.

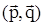 , зная их разложение по трем единичным взаимно перпендикулярным векторам
, зная их разложение по трем единичным взаимно перпендикулярным векторам 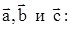
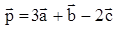 ;
; 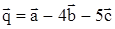 .
.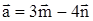 , зная, что
, зная, что  – взаимно перпендику-
– взаимно перпендику- попарно образуют друг с другом углы, каждый из которых равен
попарно образуют друг с другом углы, каждый из которых равен  . Зная, что
. Зная, что 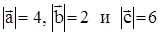 , определить модуль вектора
, определить модуль вектора  .
. перпендикулярен к вектору
перпендикулярен к вектору 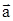 .
.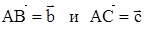 , совпадающие со сторонами треугольника АВС. Найти разложение вектора, приложенного к вершине В этого треугольника и совпадающего с его высотой BD по базису
, совпадающие со сторонами треугольника АВС. Найти разложение вектора, приложенного к вершине В этого треугольника и совпадающего с его высотой BD по базису 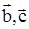 .
.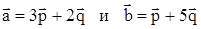 , где
, где 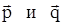 - единичные взаимно перпендикулярные векторы.
- единичные взаимно перпендикулярные векторы.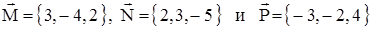 , приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения
, приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения  в положение
в положение 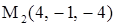 .
.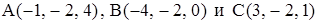 . Определить его внутренний угол при вершине В.
. Определить его внутренний угол при вершине В.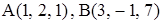 ,
, 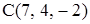 , убедиться, что этот треугольник равнобедренный.
, убедиться, что этот треугольник равнобедренный. , зная, что он перпендикулярен векторам
, зная, что он перпендикулярен векторам 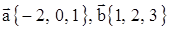 и
и  .
.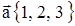 и удовлетворяющий условию
и удовлетворяющий условию  , где
, где 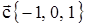 .
. на ось вектора
на ось вектора 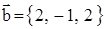 .
.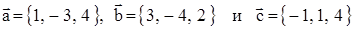 . Вычислить
. Вычислить 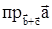 .
.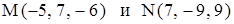 . Вычислить проекцию вектора
. Вычислить проекцию вектора  на ось вектора
на ось вектора 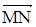 .
.


