Силовае измерения на АСМ
Кантилевер – это датчик силового взаимодействия. Любую информацию о поверхности микроскоп получает благодаря механическим отклонениям балки кантилевера, которые регистрируются оптической системой [7]. Обычно кантилевер представляет собой балку в виде прямоугольного параллелепипеда (Рис. 11) или в виде двух балок, соединенных под некоторым углом, с зондом (острием) на одном из ее концов. Далее подробно рассмотрим используемый в нашей работе прямоугольный кантилевер. С поверхностью взаимодействует острие зонда. Считаем, что именно к его вершине приложена сосредоточенная сила, действующая со стороны исследуемого образца.
Сила, действующая на зонд, зачастую имеет не только вертикальную составляющую, но и компоненты, лежащие в горизонтальной плоскости. Поэтому острие кантилевера может отклоняться не только вдоль оси, но в двух других направлениях. Вертикальную составляющую Fz назовем нормальной силой, поперечную Fx и продольную Fy - латеральными силами. Так как в АСМ о силе воздействия образца на кантилевер судят по деформации последнего, то для определения силы, необходимо знать жесткость деформаций кантилевера в различных направлениях. Считаем, что вектор отклонения острия кантилевера (имеющий компоненты Δx, Δy, Δz) связан с приложенной к зонду силой линейно, т.е. по закону Гука:
Коэффициентом пропорциональности служит тензор второго ранга, который назовем тензором обратной жесткости. Эта величина содержит всю информацию об упругих свойствах кантилевера. Чтобы найти компоненты тензора C, необходимо решить задачи о статических деформациях кантилевера под действием сил, направленных по разным осям. Для наглядности запишем формулу (1) в матричном виде:
При силовых измерениях главный интерес представляет деформация кантилевера под действием вертикальной силы. Определим величину и направление этой деформации. Решение этой задачи позволит найти последний столбец тензора С:
Деформация вертикального изгиба показана на Рис. 12:
Выделим из балки двумя поперечными сечениями элемент длиной и рассмотрим его деформацию (Рис. 14). Так как этот элемент изогнут, то материал на внешней стороне изгиба растянут, а на внутренней стороне сжат. Но имеется нейтральная поверхность, которая и не сжата и не растянута. Для упрощения вычислений будем считать, что поперечные сечения балки остаются плоскими и нормальными к её деформированной оси (прямой чистый изгиб балки постоянного сечения).
Для чистого изгиба нейтральная поверхность проходит через центр тяжести поперечного сечения, т.е. в нашем случае продольная ось симметрии параллелепипеда принадлежит нейтральной поверхности. Продольное удлинение материала ΔL пропорционально расстоянию z от нейтральной поверхности:
Величину
Обозначим отклонение в z-направлении точки балки на расстоянии y от закреплённого конца через u(y). Кривизна кривой u(y) при малых изгибах
С другой стороны, Mz является моментом сил относительно точки y, обусловленным действием силы Fz и собственным весом балки. Таким образом, получаем уравнение:
Интегрируя его с учетом граничных условий
Отклонение конца балки Δz (Рис. 12):
Второе слагаемое - это прогиб под действием собственного веса. Для типичного кантилевера он составляет доли ангстрем и может быть опущен на фоне первого члена, который в АСМ-экспериментах в сотни раз больше. Зависимость (11) есть ни что иное, как соотношение (5), в котором надо положить:
Коэффициент обратной жесткости
Из-за того что с является наибольшей компонентой тензора С, при силовых измерениях (кроме измерений латеральных сил) можно использовать закон Гука в простой форме:
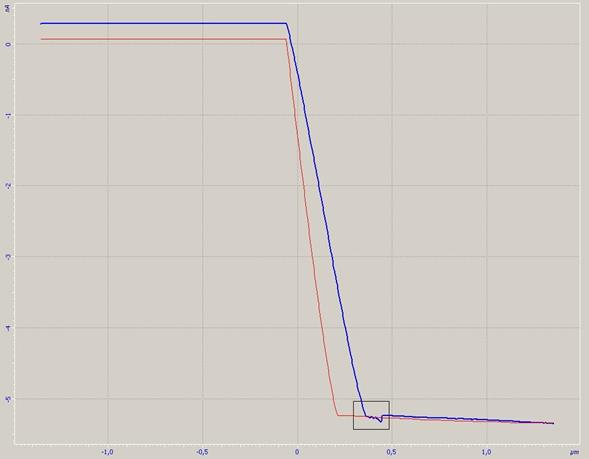
Где Для силовых измерений прямым способом в данной работе использованы контактные зонды марки HA_NC с золотым покрытием, из-за малой толщины (10-20 нм) слой золота не влияет на упругие свойства кантилевера.. Результатом силового измерения с помощью атомно-силового микроскопа являются силовые кривые, представляющие собой зависимость дифференциального тока фотоприемника (разность уровней сигнала от верхней и нижней долей приемника) от смещения основания зонда по высоте. Типичная силовая кривая, характерная для специфического взаимодействия, приведена на рис. 15.
Рис. 15. Силовые кривые. Красная – подвод зонда к подложке, синяя – отрыв зонда, черная – идеализация, выделенная область соответствует отрыву зонда от поверхности и служит для определения значения силы специфического взаимодействия.
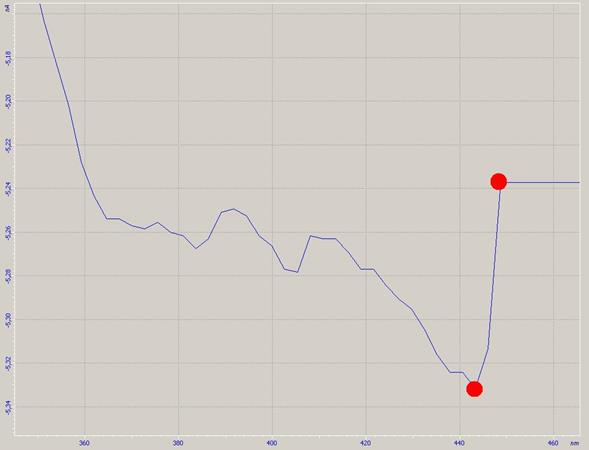
Правый горизонтальный участок соответствует подводу зонда до касания с поверхностью образца, левый горизонтальный участок не несет физического смысла и объясняется принудительным ограничением движения сканера, которое вводится для предохранения зонда от поломки при чрезмерной контактной силе. Наклонный участок кривой соответствует деформации кантилевера при уменьшении расстояния от его основания до подложки после касания ее зондом. Отличие (незначительное) его от прямой линии объясняется наличием некоторой нелинейности и дрейфа параметров в системе регистрации. Наклонный участок кривой принимаем за прямую линию и находим соответствие значения дифференциального тока деформации кантилевера. Например, для приведенной на Рис.15 кривой получается соотношение 21.6 нА/мкм. Зная соответствие между значением дифференциального тока фотоприемника и деформацией кантилевера, находим изгиб кантилевера, соответствующий отрыву зонда от поверхности (участок, выделенный прямоугольником на рис. 15, рис. 16), подставив его значение в закон Гука (14), зная силовую постоянную кантилевера, находим значение силы специфического взаимодействия.
Рис. 16. Фрагмент силовой кривой, соответствующий отрыву зонда от поверхности.
|

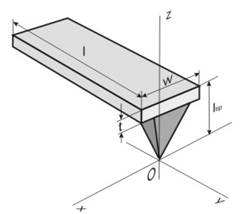 Рис. 11. Геометрия кантилевера.
Рис. 11. Геометрия кантилевера.
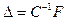

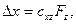
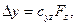
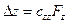
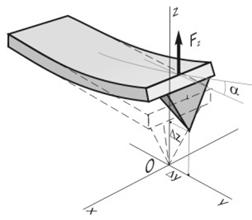 Рис. 12. Вертикальная деформация.
Рис. 12. Вертикальная деформация.
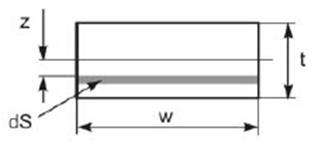 Рис. 13. Поперечное сечение.
Рис. 13. Поперечное сечение.
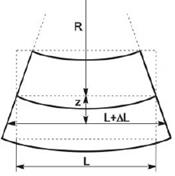 Рис. 14. Маленький отрезок внутри изогнутой балки.
Рис. 14. Маленький отрезок внутри изогнутой балки.
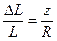 . Таким образом, по закону Гука сила, действующая на единичную площадь в некоторой маленькой полоске площадью dS вблизи z, равна
. Таким образом, по закону Гука сила, действующая на единичную площадь в некоторой маленькой полоске площадью dS вблизи z, равна  , где E - модуль Юнга, R— радиус кривизны балки. Если рассмотреть любое поперечное сечение, то действующие на нём силы направлены в одну сторону выше нейтральной поверхности и в другую - ниже её. Получается пара сил, которая создаёт изгибающий момент Mz, под которым понимают момент сил относительно нейтральной линии:
, где E - модуль Юнга, R— радиус кривизны балки. Если рассмотреть любое поперечное сечение, то действующие на нём силы направлены в одну сторону выше нейтральной поверхности и в другую - ниже её. Получается пара сил, которая создаёт изгибающий момент Mz, под которым понимают момент сил относительно нейтральной линии: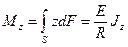
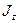 называют осевым моментом инерции сечения балки относительно оси, проходящей через его центр масс. Для балки с прямоугольным поперечным сечением:
называют осевым моментом инерции сечения балки относительно оси, проходящей через его центр масс. Для балки с прямоугольным поперечным сечением: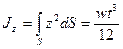
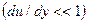 задаётся выражением
задаётся выражением 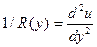 . Тогда изгибающий момент сил Mz можно выразить следующим образом:
. Тогда изгибающий момент сил Mz можно выразить следующим образом: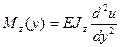
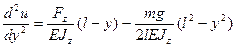
 и
и 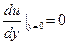 , получаем решение:
, получаем решение:
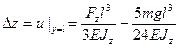
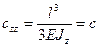
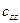 является наибольшим среди остальных компонент тензора. В формуле (12) для этого параметра введено специальное обозначение c без индексов. Именно величина
является наибольшим среди остальных компонент тензора. В формуле (12) для этого параметра введено специальное обозначение c без индексов. Именно величина 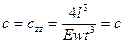
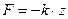
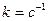 - “силовая постоянная кантилевера” – обозначение, принятое в атомно-силовой микроскопии. Законом Гука в таком виде мы будем пользоваться в дальнейшем.
- “силовая постоянная кантилевера” – обозначение, принятое в атомно-силовой микроскопии. Законом Гука в таком виде мы будем пользоваться в дальнейшем.