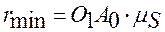Синтез кулачковых механизмов
Методические указания к курсовому проекту
Факультет производственного менеджмента и инновационных технологий: Специальности: 150405 – Машины и оборудование лесного комплекса 151001 – Технология машиностроения 190601 – Автомобили и автомобильное хозяйство
Направления: 151000.62 «Технологические машины и оборудование» 151900.62 «Конструкторско-технологическое обеспечение машиностроительных производств» 190600.62 «Эксплуатация транспортно-технологических машин и комплексов»
Вологда УДК: 621.01 (07)
Теория механизмов и машин. Синтез кулачковых механизмов: методические указания к курсовому проекту. – Вологда: ВоГТУ, 2011, - ____с.
Методические указания предназначены для студентов дневного и заочного отделений.
В методических указаниях рассмотрены примеры синтеза кулачковых механизмов с различными видами толкателей.
Утверждено: редакционно-издетельским советом ВоГТУ.
Составители: Л.Н. Рябинина, ст. преподователь.
Рецензент: О.Н.Пикалев, к.т.н., доцент ВВЕДЕНИЕ
Кулачковые механизмы, выполняющие самые различные функции, получили широкое распространение в машиностроении и приборостроении. Наиболее часто они используются как основной механизм для перемещения исполнительных звеньев или как вспомогательный механизм для управления циклом или выполнения некоторых операций: подачи, смазки, перемещения суппорта, включения двигателя т.д. Продолжительность и последовательность движений выходного звена (толкателя) в кулачковом механизме согласуется с движением других механизмов с помощью циклограмм или тактограмм, позволяющих обоснованно назначать фазовые углы поворота кулачка при удалении, сближении, дальнем и ближнем состоянии. Кулачковый механизм в большинстве случаев является составной частью общей кинематической схемы проектируемой машины. Поэтому его проектирование выполняется после того, как предварительно намечена общая компоновка машины, спроектированы ее рабочие органы, определены основные кинематические параметры движения кулачкового вала, установлена продолжительность и последовательность выполнения отдельных элементов движения ведомого звена кулачкового механизма, выбран закон его движения.
1. ОБЩИЕ СВЕДЕНИЯ
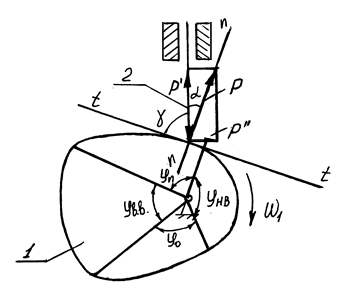
Кулачковым называется механизм, включающий высшую кинематическую пару, которую образуют кулачок и толкатель (рис. 1). Кулачком называется звено, имеющее элемент высшей кинематической пары, выполненный в виде поверхности переменной кривизны (1). Звено, образующее с кулачком высшую кинематическую пару (звено 2), и получающее возвратно-поступальное движение, называют толкателем. Если звено совершает возвратно-вращательное движение, то его называют коромысловый толкатель.
φn– угол подъема (удаления); φВВ– угол верхнего выстоя (дальнего стояния); φо– угол опускания (приближения); φnв– угол нижнего выстоя (ближнего стояния); φр = φn+ φВВ + φо – рабочий угол; α – угол давления; γ – угол передачи. Рис.1.
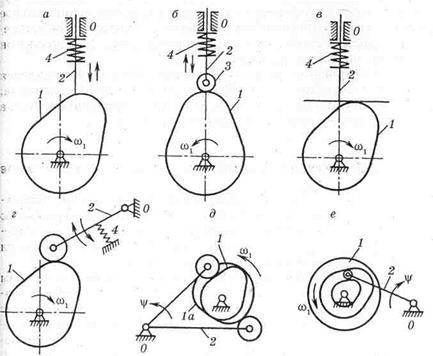
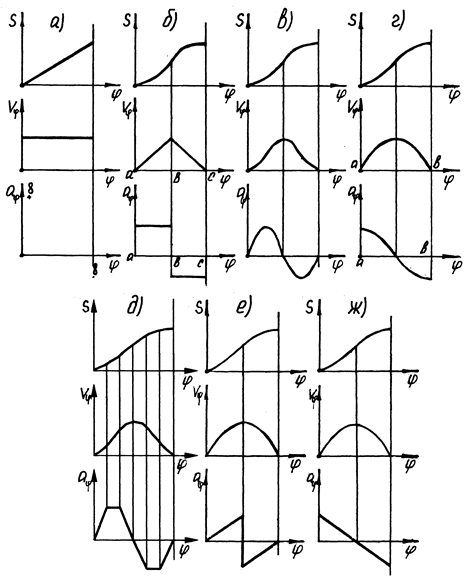
Цикл работы кулачкового механизма состоит из четырех фаз, соответствующих углам поворота кулачка: а) подъема (удаления) толкателя; б) остановки в крайнем удаленном положении (дальнего стояния или верхнего стояния); в) опускания (приближения); г) остановки в крайнем ближнем положении (ближнего стояния или нижнего выстоя). Углы подъема, верхнего выстоя, опускания в сумме образуют рабочий угол профиля кулачка. В некоторых кулачковых механизмах в зависимости от программы работы кулачка могут отсутствовать фазы верхнего и нижнего выстоя ведомого звена. Основным свойством кулачковых механизмов является возможность получения любого, наперед заданного, закона движения ведомого звена, в том числе и движения с остановками толкателя заданной продолжительности. Это свойство, присущее в основном кулачковым механизмам, является их основной отличительной особенностью и преимуществом по сравнению с другими механизмами. К недостаткам кулачковых механизмов относятся: 1. Большие удельные давления в элементах высшей кине-матической пары, что влечет за собой увеличение износа от сил трения и уменьшение к.п.д.; 2. Относительная технологическая сложность и высокая стоимость изготовления профиля кулачка. Кулачковые механизмы подразделяются на плоские и пространственные. К плоским относятся механизмы, точки звеньев которых перемещаются в параллельных плоскостях. Основным критерием классификации кулачковых механизмов является характер движения толкателя. По этому признаку все механизмы с ведущим кулачком (как плоские, так и пространственные) делятся на три типа: 1) с поступательным движением толкателя; (рис. 2 а, б, в) 2) с качающимся движением толкателя; (рис. 2 г, д, е) 3) со сложным движением толкателя. (рис. 2 ж) Механизмы первого типа отличаются более простой по сравнению с механизмами других типов конструкцией и применяются во многих машинах (например, в двигателях внутреннего сгорания автомобилей и тракторов). Лучшими эксплуатационными характеристиками обладают механизмы второго типа, чем и объясняется их наиболее широкое распространение в технике. Механизмы третьего типа, не имея преимущества по сравнению с первыми, сложнее их по конструкции, поэтому применять такие механизмы, не рекомендуется, и в машинах они встречаются редко.
Кулачковые механизмы бывают либо с вращающимся кулачком, либо с поступательно движущимся кулачком (последние встречаются редко). Толкатели бывают различных видов: остроконечный (рис. 2а), роликовый (рис. 2б, г, д, е), грибовидный (сферический), тарельчатый (плоский)(рис. 2в).
Во время работы кулачкового механизма возникают инерционные усилия, направленные на отрыв рабочей поверхности толкателя от профиля кулачка. Поэтому одним из важнейших требований к кулачковым механизмам является то, что кулачок и толкатель должны быть постоянно в соприкосновении, т.е. они должны быть замкнуты. Различают силовое замыкание, осуществляемое чаще всего с помощью пружины(рис. 2 а, б, в, г), и кинематическое (геометрическое) – осуществляемое профилем кулачка (например, ролик перемещается по пазу кулачка) (рис. 2 г, д). При геометрическом замыкании высшей кинематической пары кулачок является ведущим звеном как на фазе удаления толкателя, так и на фазе его возвращения. При силовом замыкании высшей кинематической пары движение толкателя на фазе опускания (возвращения) толкателя происходит под действием силы упругости пружины (силы тяжести или давления воздуха и т.п.), а на фазе подъема (удаления) – под действием движущей силы R¢12. Как видно из рис. 1, эта сила является вертикальной составляющей силы R12 нормального давления со стороны кулачка, на толкатель. Законы движения толкателя, определяющие профиль кулачка, задаются при проектировании кулачкового механизма в зависимости от требований технологического процесса, при этом возможны варианты: • толкатель должен перемещаться по определенному закону, связанному с выполнением технологической операции(например, рабочие органы в станках автоматах); • толкатель должен перемещаться на заданную величину хода за определенное время, при этом закон движения не влияет на технологический процесс. В первом случае закон движения толкателя однозначно определяется технологическим процессом, а во втором случае его задает конструктор с учетом заданных условий (ход, скорость вращения кулачка). При прочих равных условиях выбирается такой закон перемещения толкателя, при котором обеспечивают наилучшие условия работы механизма. В большинстве случаев стремятся задать движение толкателя с наименьшими ускорениями, что позволяет работать с наименьшими нагрузками. В результате уменьшаются силы инерции и реакции к кинематических парах, а, следовательно, их износ, потери на трение, а так же вибрации и шум при эксплуатации машин. Обычно закон движения толкателя задается в виде аналога ускорения толкателя в зависимости от угла поворота кулачка. Принципиально возможны любые законы движения толкателя, но на практике используют только те законы, которые требуют простую технологию изготовления кулачка и удов-летворяют кинематическим и динамическим требованиям. К таким законам относятся: (рис. 3) линейный (а), равноускоренный (б), синусоидальный (в), косинусоидальный (г), трапециедальный (д), линейно-возрастающий (е) и линейно – убывающий (ж). При линейном законе скорость движения толкателя на фазах удаления и приближения постоянна, а ускорение равно нулю, но в начале и в конце фаз ускорение теоретически стремится к бесконечности. Такое изменение ускорения, а следовательно, и силы инерции толкателя вызывает «жесткий удар». При этом звенья механизма подвергаются деформации и интенсивному неравномерному изнашиванию. Линейный закон допустим лишь при малых массах толкателя и малых скоростях движения. В законах, по которым скорость изменяется непрерывно, а аналог ускорения имеет точки разрыва (косинусоидальный, равноускоренный, линейно - убывающий, линейно – возраста-ющий), ускорение и силы инерции толкателя мгновенно изменяются на конечную величину и вызывают «мягкие удары».
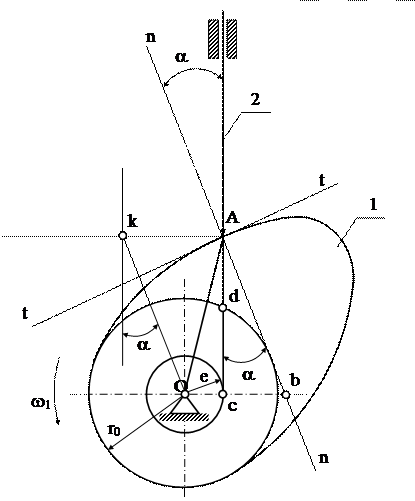
Рис. 3. Законы движения толкателя: линейный (а), равноускоренный (б), синусоидальный (в), косинусоидальный (г), трапециедальный (д), линейно-возрастающий (е) и линейно – убывающий (ж). К безударным относятся законы, согласно которым аналог ускорения является непрерывной функцией (синусоидальный, трапециедальный). Одним из важнейших расчетных параметров кулачкового механизма является угол давления. Угол a (рис.1), образуемый общей нормалью n–n к про-филю кулачка в точке касания с толкателем, по которой действует сила реакции со стороны кулачка на толкатель, и направлением скорости точ ки толкателя называется углом давления. Сила R12 может быть разложена на две составляющие: силу R¢12= R12×cosa, действующую вдоль линии движения толкателя, и силу R¢¢12= R12×sina, направленную по перпендикуляру к линии движения толкателя. Сила R¢12 является полезной силой, направленной на преодоление сил сопротивления, а сила R¢¢12 – вызывает перекос толкателя, возникновение сил трения в направляющих толкателя. Если эта сила велика, то возникающие в направляющих силы трения могут превысить силу R´12 и тогда произойдет заклинивание толкателя. Чем больше угол давления a, – тем больше сила R¢¢12. Исходя из этого, на практике при проектировании кулачкового механизма максимальные значения углов давления ограничивают. Для поступательно движущихся толкателей [a ] = 30° ¸ 40°, для вращающихся толкателей [a ] = 40° ¸ 50°. Проектирование кулачкового механизма сводится к определению минимального радиуса кулачка rmin, который должен быть таким, чтобы угол давления a не превышал допустимой величины [a ] в любом положении механизма. Для решения поставленной задачи удобно пользоваться перемещением толкателя s2, аналогами скорости (ds2/dφ1) и ускорения (d²s2/dφ1²). Эти параметры имеют размерность длины, следовательно, могут быть изображены не условно, а в виде отрезков. Рассмотрим связь между углом давления и размерами кулачка (рис. 4). Построим план скоростей для кулачкового механизма
VA2= VA1+ VA2A1, VA1=ω1∙ОА ⊥ ОА, VA2A1 ‖ t–t, VA2 ‖ направляющей толкателя.
Рис. 4.
Проведем через ось вращения кулачка линию перпен-дикулярную направлению движения толкателя до пересечения с нормалью. Получим отрезок Ов. Треугольник ОА в подобен треугольнику плана скоростей. Из подобия:
Отсюда О в =ds2/dφ, т.е. отрезок О в является аналогом скорости толкателя для данного положения механизма.
Если продолжить линию толкателя, то получим угол ее с линией АB, равный α. tgα = сb/сА=сb/(cd+dA), где dA = s2 – перемещение толкателя.
После подстановок получим, что
Если е = 0, т.е. кулачковый механизм центральный, то
Из равенств следует, что при выбранном законе движения и эксцентриситете е габариты кулачка определяются радиусом r0 окружности минимального радиуса кулачка. Увеличивая r0 , мы получаем меньшие углы давления α, но большие габариты кулачкового механизма, и наоборот, при уменьшении r0 возрастают углы давления α и уменьшается к.п.д. механизма. Если из точки А отложить отрезок Аk = O в повернутый на 900 по вращению кулачка аналог скорости толкателя, и соединить точку k с центром вращения кулачка О, то соединительная прямая Оk составит с линией толкателя угол, равный углу давления в данном положении механизма. Таким образом, для определения угла давления не нужно знать профиль кулачка. Достаточно определить по заданному закону движения значение величины аналога скорости и отложить этот отрезок от данного положения оси вращения ролика А в направлении, перпендикулярном направлении ее скорости, и соединить прямой линией конец отрезка с осью вращения кулачка. Угол между этой линией и направлением скорости оси ролика и есть угол давления. Если из точки А отложить отрезок Аk=Оb и через точку k провести луч под углом a к направлению движения толкателя, то он пройдет через центр вращения кулачка. При проектировании механизма когда размеры кулачка, его радиус r0 не известны, положение оси вращения кулачка так же будет не известно. Его выбирают таким образом, чтобы любое из текущих значений угла давления α не превышало допустимого значения [α]. Для этого строят фазовый портрет, т.е. зависимость s2=f(ds2/dφ1) (рис. 5).
Рис. 5.
Для механизма с поступательно перемещающимся толкателем построить ОДР существенно проще: достаточно провести всего два луча. касательных к фазовому портрету под углом [α]. Заштрихованная зона, ниже точки О1 (рис. 5), является зоной кинематического замыкания. При выборе оси вращения кулачка в этой зоне всегда удовлетворяется условие, в соответствии с которым угол давления в любом положении механизма меньше [a].
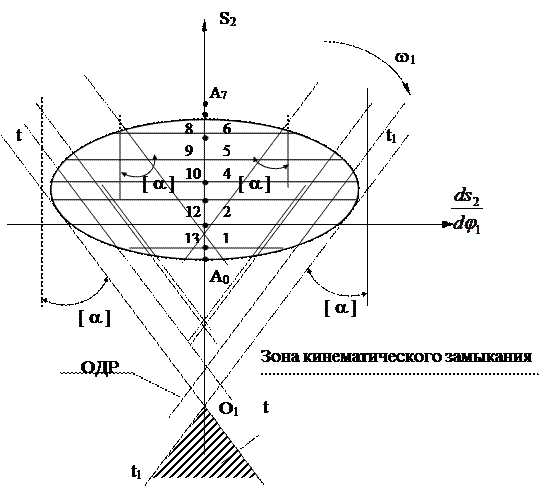
Для механизма с качающимся толкателем (коромыслом) рассуждения подобны изложенным выше. Для определения r0 также строится фазовый портрет (зависимость ds2/dφ1=f(s2)), но в полярных координатах (рис. 6). Направление отрезков аналога скоростей также определяется по правилу векторного произведения. Через концы отрезков – аналогов скоростей проводят прямые под углом [a] к нормалям и определяют точку наиболее удаленную от нижнего положения толкателя (рис. 6). Расстояние от точки О1 до точки А0 является минимальным радиусом кулачка.
Рис. 6
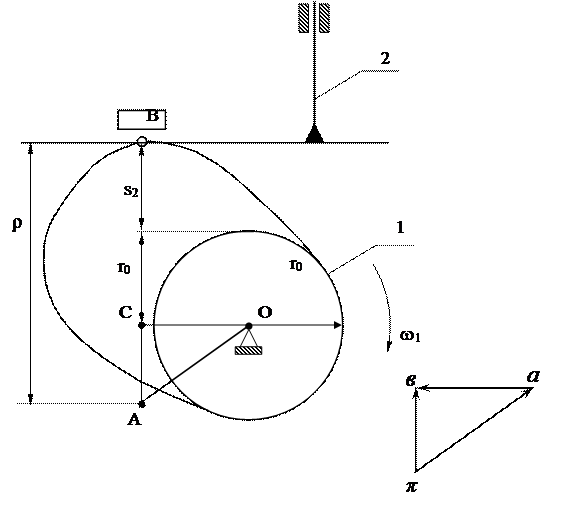
При качающемся толкателе нельзя проводить касательные к кривой ds2/dφ1=f(s2), так как отрезки – аналоги скоростей толкателя не параллельны. При инженерных расчетах для определения минимального радиуса кулачка с качающимся толкателем достаточно провести наклонные прямые под углом [α] через точки соответствующие максимальным значениям аналога скорости. Особенностью проектирования кулачкового механизма с плоским (тарельчатым) толкателем является то, что угол давления в них является постоянным, а в частном случае, когда тарелка толкателя перпендикулярна оси толкателя, угол давления α становится равным нулю. Для кулачковых механизмов данного вида должно удовлетворяться дополнительное условие – кулачок должен быть выпуклым на всем контуре, т.е. не иметь точек перегиба (ρ; >0). Рассмотрим кулачковый механизм с плоским толкателем (рис. 7) и построим для заданного положения заменяющий механизм (ОАВ) и план ускорений.
Рис.7
Из точки О опускаем перпендикуляр на линию АВ. ∆ОАС ∞ ∆π в1в2. Отсюда:
Таким образом: Из рисунка (6) находим ρ; = s2 + r0 + АС, где r0 – минимальный радиус кулачка s2 – перемещение толкателя
Отсюда
Разделим обе части неравенства (1.2) на (s2 + r0)
или
По условию (1.4) строится график s2 = f(d²s2/dφ1²). Под углом 45° к оси s проводится касательная к кривой на участке, где d²s2/dφ1² < 0. За центр вращения кулачка принимается любая точка лежащая ниже точки пересечения касательной с осью s. Второй метод определения r0 для кулачкового механизма с плоским толкателем сводится к решению неравенства (1.1) относительно r0. Т.е. r0 больше наибольшей отрицательной ординаты суммарного графика
2. ГРАФИЧЕСКИЙ МЕТОД ДИНАМИЧЕСКОГО СИНТЕЗА КУЛАЧКОВОГО МЕХАНИЗМА С ПОСТУПАТЕЛЬНО ДВИЖУЩИМСЯ РОЛИКОВЫМ И ОСТРОКОНЕЧНЫМ ТОЛКАТЕЛЕМ (Приложение 1,2).
2.1. Построение кинематических диаграмм
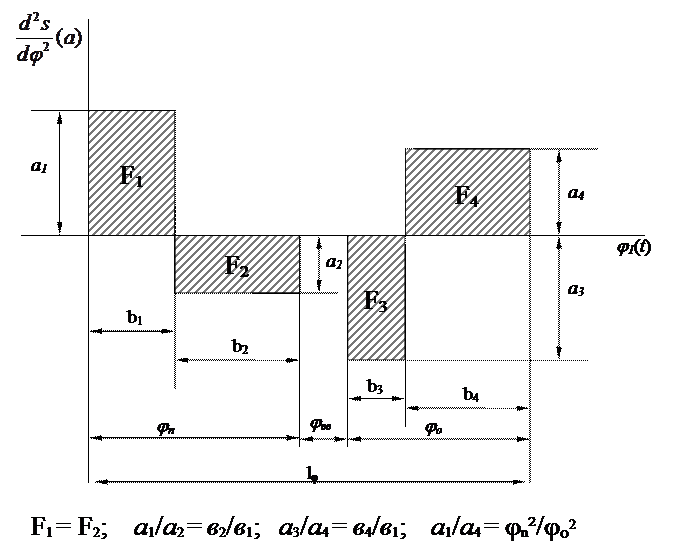
Проектирование кулачкового механизма начинают с построения кинематических диаграмм аналогов ускорения и скорости, а также перемещения. Исходными данными для построения диаграмм могут быть заданный закон изменения аналога ускорения, максимальное и минимальное значения аналога ускорения (или их отношение), рабочий угол профиля кулачка, фазовые углы, угловая скорость кулачка. По данным для проектирования строится диаграмма изменения аналогов ускорений (рис.8). По оси ординат желательно отложить отрезок, изображающий максимальное значение аналога ускорения, равный 70–80 мм. По оси абсцисс откладывается рабочий угол профиля ведущего звена кулачка. Рекомендуется принять отрезок ℓ φ, изображающий рабочий угол профиля кулачка, равным 180–300 мм. В том случае, когда задано отношение максимального аналога ускорения к минимальному y=а 1 /а 2, а углы подъема (удаления) и опускания (приближения) не равны, но законы для них одинаковы, то при построении диаграммы необходимо выдержать равенство площадей F1=F2, F3=F4, (рис.7) т.е. а 1 /а 2 =в 2 /в 1; а 3 /а 4 =в 4 /в 3. Кроме того должно выполняться равенство а 1 /а4 = φn²/φy². Построение кинематических диаграмм на конкретном примере рассмотрено в приложении1. Построив заданную диаграмму аналога ускорений толкателя в зависимости от угла поворота кулачка (d2s/dφ12=f(φ1)) и графически проинтегрировав ее, получим диаграмму аналога скорости толкателя в зависимости от угла поворота кулачка ds2/dφ1=f(φ1).
Метод графического интегрирования заключается в следующем. Углы подъема и опускания диаграммы d2s2/dφ1=f(φ1) разбиваем по оси φ на 8¸10 участков (0–1; 1–2; 2–3; и т.д.) и плавную кривую заменяем ступенчатой из условия равенства площадей, ограниченных обеими диаграммами. Для этого необходимо, чтобы на каждом участке площади заштрихованных площадок, расположенных по обе стороны кривой, были равны. Это достаточно точно устанавливается на глаз. Выбираем на оси абсцисс слева от начала координат на произвольном расстоянии H а точку р. Соединим эту точку с точками 1¢¢, 2¢¢, 3¢¢ и т.д. ступенчатой диаграммы лежащими на оси ординат, получим лучи р –1¢¢; р –2¢¢; р –3¢¢; и т.д.
Под диаграммой d2s2/dφ12=f(φ1) проводим оси координат диаграммы ds2/dφ1=f(φ1) и разбиваем ось φ на участки, равные соответствующим участкам диаграммы d2s2/dφ12=f(φ1). Далее на участке 0–1 проводим из начала координат отрезок 0–1¢, параллельный лучу р –1¢¢; из полученной точки 1¢ на участке 1–2 проводим отрезок 1¢–2¢ параллельный р –2¢¢; из точки 2¢ проводим отрезок 2¢–3¢, параллельный лучу р –3¢¢ и т.д. Полученная ломаная линия представляет собой диаграмму ds2/dφ1=f(φ1) (аналога скорости толкателя в функции угла поворота кулачка). Заменяем ломаную линию плавной кривой и еще раз графически интегрируем, выбрав по возможности полюсное расстояние Масштабные коэффициенты диаграмм определяются следующим образом:
где h – заданный ход толкателя, в м; smax – максимальная ордината диаграммы s2=f(φ1), в мм;
где φр = φу + φ вв + φп – рабочий угол профиля в рад.; ℓφ – отрезок, изображающий рабочий угол на диаграмме, в мм; H V – полюсное расстояние.
где Hа – полюсное расстояние, в мм.
В том случае, когда ωкул.=const полученные диаграммы одновременно являются диаграммами ускорения (а 2=f(t)), скорости (V2=f(t)) и перемещения (s2=f(t)) толкателя. Масштабные коэффициенты этих диаграмм определяются:
где ω1=ωкул. – угловая скорость кулачка;
2.2. Определение минимального радиуса кулачка
При определении минимального радиуса профиля кулачка необходимо построить диаграмму зависимости s2=f(ds2/dφ1). При этом следует обеспечить равенство масштабных коэффициентов по осям координат. Это условие выполняется автоматически, если при графическом интегрировании берется HV= 1/μφ. Когда HV выбрано произвольно, то для приведения отрезков аналогов скоростей к масштабному коэффициенту перемещений можно воспользоваться следующим методом: каждую величину ординаты диаграммы аналогов скоростей умножают на отношение масштабных коэффициентов μds/dφ / μs. По оси ординат в масштабе μs отложим от начала координат перемещения толкателя, согласно построенному графику s2=f(φ1). Через полученные точки 0, 1, 2… и т.д. проводим прямые параллельные оси абсцисс. На этих прямых отложим отрезки равные ds2/dφ1, в масштабе μds/dφ = μs. Причем, для фазы подъема (удаления) эти отрезки откладываются в сторону вращения кулачка, а для фазы опускания – в обратную, т.е. если направление вращения кулачка по часовой стрелке, то значения аналога скорости, соответствующее углу подъема, откладывается вправо, а если против часовой стрелки - то влево. Соединяем плавной кривой концы этих отрезков и получаем кривую s2= f(ds2/dφ1).
Проводим под углом давления [a ] к оси s две касательные t–t и t1–t1 к построенной кривой. Отрезок [О1А0∙μs]=rmin – минимальный радиус кулачка центрального механизма, а заштрихованная зона является зоной кинематического замыкания кулачковой пары. Выбор оси вращения кулачка в этой зоне гарантирует, что amax будет меньше [a ]. При нецентральном кулачковым механизме для определения минимального радиуса профиля кулачка необходимо на расстоянии е ¢ = е / μs [мм] (е – эксцентриситет) от оси s в соответствии со схемой кулачкового механизма провести прямую параллельно оси s (справа, если линия перемещения толкателя находится слева от оси вращения кулачка и наоборот) до пересечения в т. О2 с одной из касательных. Отрезок (О2А0) μS является минимальным радиусом rmin кулачка при заданном эксцентриситете и кинематическом замыкании кулачковой пары. При этом кулачковый механизм как и в первом случае (центральный) может быть реверсивным (вращение кулачка в обе стороны). Если эксцентриситет отложен в сторону угла удаления (подъема) и кулачковый механизм одностороннего вращения, то можно для уменьшения габаритов кулачка воспользоваться зоной силового замыкания. Из точки А проводим прямую под углом [a ] к оси s в сторону угла подъема (удаления). Зона, заштрихованная горизонтальными прямыми, является зоной силового замыкания, а отрезок (О3А0)∙μs – минимальный радиус кулачка при силовом замыкании. При выборе оси вращения кулачка в этой зоне условие αmax ≤ [a] выполняется только на фазе подъема.
2.3. Построение профиля кулачка
При построении профиля кулачка применяется метод обращения движения (инверсии). Этот метод состоит в следующем: мысленно придаем всему механизму вращение вокруг центра вращения кулачка с угловой скоростью (-ωкул), равной, но противоположно направленной действительной скорости кулачка. Тогда угловая скорость кулачка становится равной ωкул+(- ωкул)=0, то есть кулачок в обращенном движении становится неподвижным. Толкатель, если он в действительном движении перемещался поступательно, то в обращенном движении помимо своего абсолютного движения приобретает вместе со своими неподвижными направляющими добавочное движение – вращение вокруг оси А кулачка с угловой скоростью, равной(-ωкул). При этом относительное расположение толкателя и кулачка не нарушается. Профилирование нецентрального кулачка ведем в следующей последовательности: · выбираем положение центра вращения кулачка О2 (замыкание – силовое) и в масштабе μS описываем окружности радиусами, равными rmin и е; · касательно к окружности радиуса е проведем линию движения толкателя y–y, согласно ее положению на диаграмме s2=f(ds2/dφ1). Точка пересечения А0 этой прямой с окружностью rmin определит положение центра ролика, соответствующее началу подъема (удаления); · от точки А0 вдоль линии y–y откладываем перемещение толкателя, согласно графику s2=f(φ1). Точка А8 определит положение центра ролика, соответствующее концу подъема; · от прямой О2А8 в сторону, противоположную вращению кулачка, отложим фазовые углы φn, φ вв и φ о; · проводим окружность радиуса rmax= О2А8 и разделим дуги, стягивающие фазовые углы φn и φ о на части, согласно делению этих углов на графике s2=f(φ1); · через полученные точки деления 1, 2, 3, 4 и т.д. проводим касательные к окружности радиуса е, следя за тем, чтобы все касательные располагались по ту же сторону от центра О2, что и прямая y–y; · из центра вращения кулачка О2 радиусами О2А1, О2А2, О2 А3 и т.д. проведем концентрические дуги до пересечения с соответствующими касательными. Точки пересечения 1¢, 2¢, 3¢ и т.д. представляют собой положение центра ролика в обращенном механизме; · соединим полученные точки плавной кривой, получим теоретический профиль кулачка; · определим радиус ролика rр. Во избежание самопересечения практического профиля кулачка радиус ролика должен быть меньше минимального радиуса кривизны теоретического профиля кулачка rр≤(0,7¸0,8)ρmin. Радиус ролика не рекомендуется также брать больше половины минимального радиуса кулачка rmin из конструктивных соображений rр≤(0,4¸0,5) rmin.
Используя теоретический профиль кулачка как геометрическое место точек центра вращения ролика, проводим дуги радиусом rp,. Огибающая кривая этих дуг определит действительный профиль кулачка.
3. ГРАФИЧЕСКИЙ МЕТОД ДИНАМИЧЕСКОГО СИНТЕЗА КУЛАЧКОВОГО МЕХАНИЗМА С КАЧАЮЩИМСЯ ТОЛКАТЕЛЕМ (Приложение 3)
3.1. Построение кинематических диаграмм
Построение кинематических диаграмм смотри раздел 2.1. Для определения масштабного коэффициента
где
Диаграмма s2=f(φ1) одновременно является диаграммой углового перемещения толкателя (коромысла). Масштабный коэффициент определяется:
где ψmax - максимальный угол размаха коромысла (толкателя) в рад. smax - максимальная ордината диаграммы s2=f(φ1), в мм.
Масштабный коэффициент аналога угловой скорости толкателя
Масштабный коэффициент угловой скорости толкателя
Масштабный коэффициент аналога углового ускорения толкателя
Масштабный коэффициент углового ускорения толкателя
3.2. Определение минимального радиуса теоретического профиля кулачка с качающимся толкателем
Для кулачкового механизма с качающимся толкателем кривая s2=f(ds2/dφ1) строится в полярных координатах. Выбираем произвольную точку О2 и проводим направление оси толкателя О2А0 в его наинизшем положении. Отрезок О2А определяем
Проводим из точки О2 дугу радиусом О2А и откладываем на ней дуговые отрезки перемещений в соответствии с графиком s2=f(φ1) не забывая при этом, что масштабные коэффициенты, в которых отложены длина толкателя, перемещение и аналоги скорости должны быть одинаковы,
Через точки деления проводят лучи из центра вращения толкателя (О2). На лучах откладываются соответствующие значения аналогов скорости. Если направление вращения кулачка по часовой стрелке, то значения аналогов скорости, соответствующие углу подъема откладываются вправо от оси s, а если ωкул против часовой стрелки то – влево. Полученные точки 1’, 2’, 3’, …, 12’ соединяем плавной кривой и получаем искомую диаграмму s2=f(ds2/dφ1). В точках, где аналоги скорости имеют максимальное значение, проводим прямые под углом [α ]. к направлению скорости точки В толкателя. Заштрихованная зона является областью допустимых положений оси вращения кулачка. Выбор оси вращения в точке О1 определяет минимальные габариты кулачкового механизма при кинематическом замыкании (кулачковый механизм реверсивный). Отрезок О1А0 – минимальный радиус основной шайбы кулачка в масштабе μs.
3.3. Профилирование кулачка с качающимся толкателем
При профилировании кулачка используем метод обращения движения (см. п. 2.3). На чертеже выбираем точку О1 – центр вращения кулачка. Из этой точки с учетом масштабного коэффициента проводим окружность радиусом rmin, равным минимальному радиусу кулачка и окружность радиусом, равным межосевому расстоянию О1О2. Определяем положение т. О2º и от линии О1О2º в сторону противоположную направлению вращения кулачка откладываем углы равные углам профиля кулачка. Затем дуги, стягивающие эти углы делим на столько равных частей, на сколько углы разделены на кинематических диаграммах и получаем точки О2¹, О2², …, О217 (положение центра вращения толкателя в обращенном движении). Из точки О2º проводим дугу А0А8 радиусом, рав
|

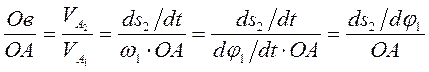

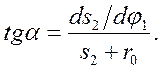
 Направление отрезков – аналогов скоростей определяется по правилу векторного произведения
Направление отрезков – аналогов скоростей определяется по правилу векторного произведения  При вращении против часовой стрелки значения аналогов скоростей соответствующие фазе удаления (подъема) откладываются слева, а отрезки соответ-ствующие фазе приближения (опускания) – справа. В каждой i-й позиции проводят через конец отрезка аналога скорости толкателя (кинематической передаточной функции скорости) ds2/dφ1 луч под углом [α] к вектору скорости в этой точке. При расположении центра вращения кулачка выполняется равенство α =[α]. Фактически угол делит плоскость, в которой может быть расположен центр вращения кулачка, на две области – допустимую, в которой αi< [α], и недопустимую, в которой αi>[α]. Проделав аналогичные построения для всех точек фазового портрета, выделяют область допустимых решений (ОДР), в любой точке которой выполняется условие αi< [α]. Центр вращения кулачка помещают в ОДР, общую для всех положений. Такое решение обеспечивает выполнение условия αi< [α] для полного цикла работы механизма.
При вращении против часовой стрелки значения аналогов скоростей соответствующие фазе удаления (подъема) откладываются слева, а отрезки соответ-ствующие фазе приближения (опускания) – справа. В каждой i-й позиции проводят через конец отрезка аналога скорости толкателя (кинематической передаточной функции скорости) ds2/dφ1 луч под углом [α] к вектору скорости в этой точке. При расположении центра вращения кулачка выполняется равенство α =[α]. Фактически угол делит плоскость, в которой может быть расположен центр вращения кулачка, на две области – допустимую, в которой αi< [α], и недопустимую, в которой αi>[α]. Проделав аналогичные построения для всех точек фазового портрета, выделяют область допустимых решений (ОДР), в любой точке которой выполняется условие αi< [α]. Центр вращения кулачка помещают в ОДР, общую для всех положений. Такое решение обеспечивает выполнение условия αi< [α] для полного цикла работы механизма.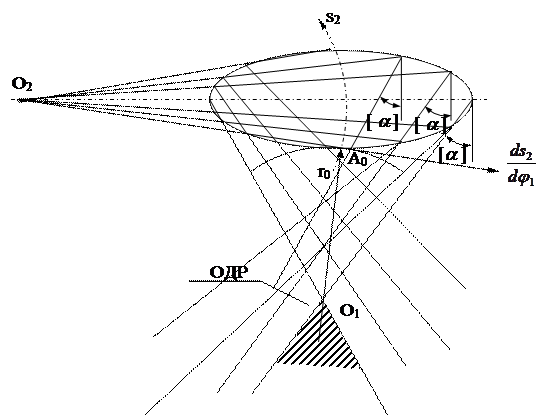
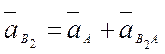
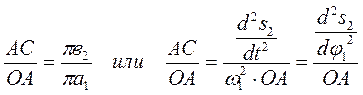
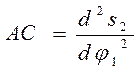 .
.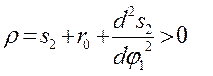 (1.1)
(1.1)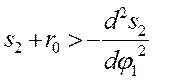 (1.2)
(1.2)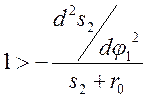 (1.3)
(1.3)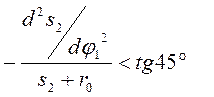 (1.4)
(1.4)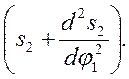
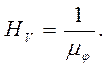 Полученная кривая – зависимость перемещения толкателя от угла поворота кулачка (s2=f(φ1)).
Полученная кривая – зависимость перемещения толкателя от угла поворота кулачка (s2=f(φ1)).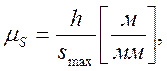
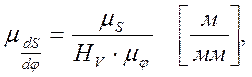
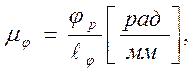
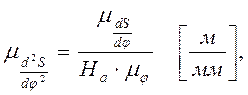
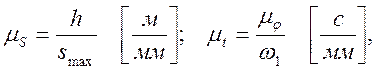
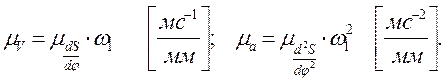
 Для отыскания ρmin поступим следующим образом: выберем на выпуклой части теоретического профиля кулачка точку k (рис. 9), в которой кривизна кривой кажется на глаз наибольшей. Затем вблизи точки k выберем еще две точки k´ и k´´ и соединим их с точкой k. Через середины полученных хорд проведем к ним перпендикуляры. Точка пересечения перпендикуляров М – центр окружности, проходящей через все три точки. Радиус этого круга приближенно можно принять за ρmin.
Для отыскания ρmin поступим следующим образом: выберем на выпуклой части теоретического профиля кулачка точку k (рис. 9), в которой кривизна кривой кажется на глаз наибольшей. Затем вблизи точки k выберем еще две точки k´ и k´´ и соединим их с точкой k. Через середины полученных хорд проведем к ним перпендикуляры. Точка пересечения перпендикуляров М – центр окружности, проходящей через все три точки. Радиус этого круга приближенно можно принять за ρmin.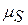 определим ход толкателя по дуге.
определим ход толкателя по дуге.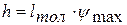 ,
,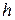 - ход толкателя (м),
- ход толкателя (м), 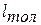 - длина толкателя (м),
- длина толкателя (м),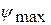 - максимальный угол размаха толкателя (рад).
- максимальный угол размаха толкателя (рад).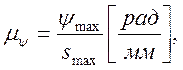
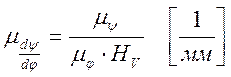 .
.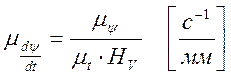 .
. .
.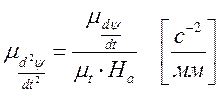 .
.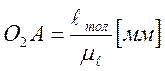 .
.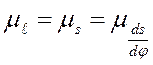 .
.