Критерии оптимальности
Введение Зубчатые механизмы, в которых имеются колеса с движущимися геометрическими осями, называются эпициклическими. Если степень подвижности такого механизма равна единице, то механизм называется планетарным, если же степень подвижности более единицы - дифференциальным. Из всех видов механических передач планетарные зубчатые передачи более других снижают материалоемкость машины. Эти механизмы по сравнению с зубчатыми передачами, имеющими неподвижные оси вращения, обладают меньшими габаритными размерами и массой при равных передаточных отношениях. Однако задача проектирования планетарных передач является более трудоемкой и объемной по времени, чем проектирование обычных передач. В этих механизмах числа зубьев колес должны удовлетворять совокупности нескольких условий и ограничений. При этом число расчетных уравнений бывает меньше числа неизвестных, поэтому нельзя получить однозначного решения. Таким образом, задача определения чисел зубьев колес сводится к поиску множества вариантов, соответствующих исходным данным, и выбору оптимального. Строение планетарных редукторов В планетарном механизме колеса с движущимися геометрическими осями, которые совершают сложное движение, называются планетарными колесами или сателлитами. Подвижное звено, в котором помещены оси сателлитов, называется водилом; вращающиеся вокруг неподвижных осей колеса (с внешними или внутренними зубьями), по которым обкатываются сателлиты, называются центральными, или солнечными; неподвижное центральное колесо называется опорным. Типичным примером планетарных механизмов является соосный механизм, изображенный на рис.1, составленный из цилиндрических колес. Этот простейший механизм состоит из центрального колеса 1, вращающегося вокруг неподвижной оси О1 с угловой скоростью w1, водила Н, которое также вращается вокруг той же оси (колесо 1 и водило Н непосредственно между собой не связаны) с угловой скоростью wН, трех сателлитов 2 и опорного колеса 3. При вращении колеса 1 по движению часовой стрелки его зубья увлекают входящие с ним в зацепление зубья сателлитов 2. Но так как, с другой стороны, зубья колеса 2 находятся в зацеплении с опорным колесом 3, то сателлиты 2 поворачиваются как рычаг относительно неподвижной опоры мгновенного центра вращения (точка В). При этом оси сателлитов 2, укрепленных в подшипниках на водиле, перемещаются и заставляют вращаться водило (по движению часовой стрелки). Сателлиты при этом совершают сложное движение: вращаются вокруг собственной оси О2 (относительно водила) против движения часовой стрелки и вместе с водилом обкатываются вокруг оси колеса 1 по движению часовой стрелки.
Рис. 1.
Существует достаточно большое количество схем планетарных редукторов, но в практике машиностроения широко распространены только четыре схемы планетарных зубчатых передач (рис. 2). Преимущества и недостатки планетарных механизмов
К преимуществам можно отнести: 1) Меньший вес и габариты по сравнению с обычными зубчатыми механизмами (в 1,5…5 раз). Применяются на многих военных машинах (вездеходах), авиации, космической технике (луноходах). 2) Большой диапазон передаточных отношений (от нескольких единиц до сотен и даже тысяч). 3) Почти все подшипники разгружены (кроме сателлитных). 4) Компактность. Например, при мощности, равной 700 л. с. чертеж редуктора, выполненный в масштабе 1:1, занимает площадь формата А1. 5) Высокая надежность, малые потери на трение.
Недостатки: 1) Требования к высокой точности изготовления колес. При неточном изготовлении перегрузка составляет 1,25. Поэтому современные планетарные механизмы конструируются плавающими. В этом случае перегрузка при одном плавающем звене составляет всего 1,1, а при двух плавающих звеньях перегрузки нет. 2) Более сложная сборка. 3) Сложность конструкции.
Основные характеристики планетарных механизмов Проектирование планетарных механизмов начинают с выбора схемы механизма. При этом очень важно выбрать оптимальную схему механизма, так как для одной и той же цели одно и то же заданное передаточное отношение можно обеспечить различными схемами механизмов, которые будут резко отличаться по к.п.д., габаритам и весу. Как известно, к.п.д. планетарных передач резко уменьшается с увеличением передаточного отношения. Чтобы получить механизм с повышенным к.п.д., иногда оказывается целесообразным соединять планетарную передачу с непланетарной; для осуществления больших передаточных отношений следует последовательно соединять несколько планетарных передач. Использование внутреннего зацепления в планетарных механизмах позволяет уменьшить габариты и вес их. Поэтому правильный выбор схемы при проектировании планетарных механизмов имеет гораздо большее значение, чем при проектировании простых передач. Причем этот выбор следует начинать с простейших механизмов. Типовые планетарные редукторы с цилиндрическими колесами обычно состоят из одного или нескольких простейших планетарных механизмов (рис.2). Все они имеют соосные валы и обладают одной степенью подвижности.
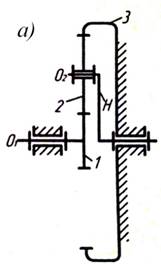
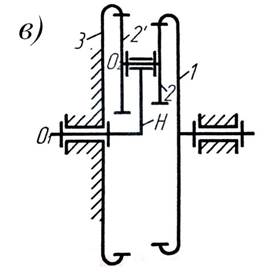
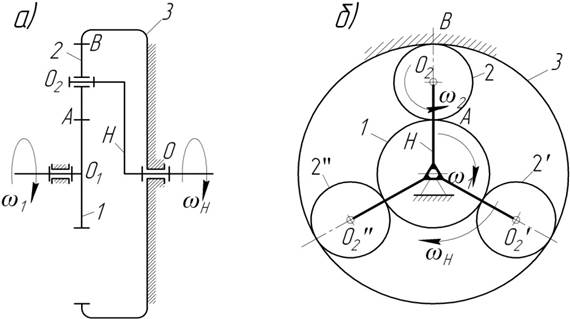
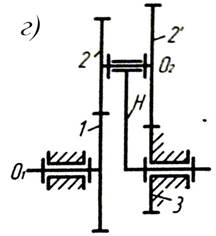
Рис. 2. В таблице 1 приведены применяемые диапазоны передаточных отношений для различных схем механизмов. Основное применение имеют механизмы, показанные на рис.2 а, б, обладающие меньшими габаритами и большим к.п.д. Они имеют широкое применение в силовых и вспомогательных приводах в качестве многосателлитных редукторов средней и большой мощности. К.п.д. таких механизмов очень высок (0,96¸0,99%). Наличие нескольких параллельно работающих сателлитов у этих редукторов позволяет передавать момент силы через несколько параллельно работающих пар зубьев и избавляет от необходимости уравновешивания сателлитов. Поэтому в таких передачах достигается значительное уменьшение размеров и веса по сравнению с другими видами передач. При выборе схемы следует учитывать, что для схем в и г, приведенных на рис. 2 передаточное отношение
Таблица 1. Рекомендации по выбору схемы планетарного механизма
Но при увеличении Синтез планетарных передач После выбора схемы механизма производят определение чисел зубьев колес так, чтобы обеспечить заданное передаточное отношение (с допустимой точностью), условие соосности, условие соседства (размещение нескольких сателлитов), условие сборки и условие отсутствия заклинивания колес передачи (условие правильного зацепления). В курсовом проекте схема планетарного механизма задается в исходных данных. Рассмотрим методику проектирования простейших схем планетарных механизмов, составленных из эвольвентных цилиндрических колес с равноделенным шагом (нулевых). При синтезе планетарных зубчатых механизмов выполняют ряд условий. 1. Первое и главное условие — передаточное отношение проектируемого редуктора должно совпадать с заданным. Следует подчеркнуть, что это совпадение не обязательно должно быть абсолютным, а может выполняться с некоторой допустимой точностью. Зачастую при обеспечении абсолютного совпадения увеличиваются габариты механизма. Допустимое отклонение передаточного отношения от заданного значения (обычно несколько процентов) согласуется с преподавателем. Передаточное отношение механизма любой схемы можно выразить через передаточное отношение механизма с неподвижным водилом, т. е. через передаточное отношение зубчатого механизма с неподвижными осями зубчатых колес (преобразованный механизм). Согласно известному соотношению: где Для схем механизмов, в которых задано передаточное отношение от водила к колесу передаточное отношение определяется по формуле:
2. Второе условие, накладывающее ограничения на выбор числа зубьев, связано с использованием в планетарном механизме зубчатых колес, нарезанных без смещения. Для исключения подрезания и заклинивания любого из колес с внешними зубьями zвнеш , нарезанных стандартным инструментом, принимают: z ≥ zmin = 17, а для колес с внутренними зубьями zвнут в зависимости от параметров долбяка принимают: z ≥ zmin = 85 при ha* = 1, z ≥ zmin = 58 при ha* = 0,8. Во избежание интерференции зубьев при внутреннем зацеплении необходимо, чтобы разность чисел зубьев в зацеплении не была слишком мала. Обычно принимают: zвнут — zвнеш ≥ 8
3. Третье обязательное условие определяется соосным расположением центральных колес планетарного механизма с водилом. Условие соосности основных звеньев сводится к равенству межосевых расстояний входящих в зацепление колес сателлита с центральным колесом и с опорным. Условие соосности, определяемое соотношением радиусов водила и начальных окружностей, для схем механизмов, изображенных на рис. 2, а–г, имеет вид: rH = rW1 + rW2 = rW3 – rW2 ; rH = rW1 + rW2 = rW3 – rW2' ; rH = rW1 – rW2 = rW3 – rW2' ; rH = rW1 + rW2 = rW3 + rW2'. При одинаковых значениях модуля зубчатых колес условие сводится к соотношениям между числами зубьев: z1 + z2 = z3 – z2 ; z1 + z2 = z3 – z2' ; z1 – z2 = z3 – z2'; z1 + z2 = z3 + z2' . Приведенные три условия не зависят от выбранного числа k сателлитов.
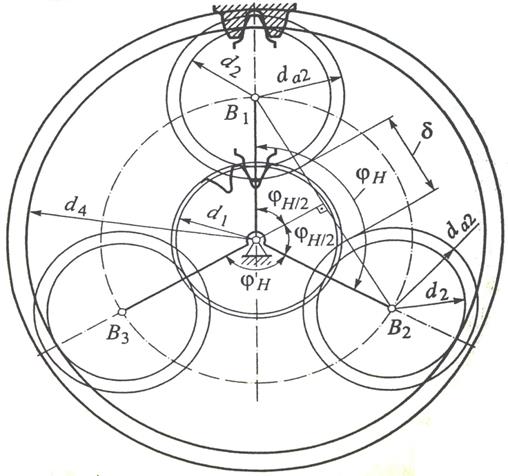
4. Четвертое условие — условие соседства, учитывающее возможность свободного размещения сателлитов без их взаимного соприкосновения, будет выполнено, если расстояние между осями сателлитов превышает диаметр da окружности вершин наибольшего сателлита (рис. 3). Для механизмов, представленных на рис. 2, это условие выражается неравенством:
где z2 (z2¢) — число зубьев большего сателлита: z2, если z2 > z2¢, и, наоборот, z2¢, если z2 < z2¢; z1 ± z2 - относительное межосевое расстояние между центральными колесами и сателлитом: z1+z2 — длявнешнего зацепления; z1–z2 — для внутреннего.
Чтобы определить наибольшее число сателлитов, которое может иметь планетарный механизм с известными числами зубьев, условие соседства приводят к виду:
5. Пятое условие связано с возможностью свободного размещения сателлитов — условие сборки. При симметрии зон зацепления это условие выражается соотношением:
где р = 0, 1, 2,... — произвольное дополнительное число оборотов водила при сборке; С — любое целое число. Выполнение этого равенства фактически означает следующее: если один из сателлитов свободно устанавливается на вертикальной оси (см. рис. 3), то все последующие сателлиты будут свободно входить в зацепление с соответствующими колесами в той же позиции. Для этого необходимо повернуть водило на угол:
Рис. 3
Здесь принято, что у двухвенцовых сателлитов, т. е. у сателлитов, состоящих из блока двух жестко скрепленных между собой зубчатых колес, в каждом блоке зубья одного венца одинаково ориентированы относительно зубьев второго венца. Необходимо также отметить, что даже в случае, если задано передаточное отношение
Все условия, которые необходимо выполнить при проектировании планетарного механизма в соответствии со схемой, сведены в таблицу 2.
Таблица 2.
При выполнении всех этих условий будет спроектирован работоспособный планетарный зубчатый механизм. Пример 1. Подобрать числа зубьев колес планетарного редуктора, схема которого приведена на рис. 2 а, передаточное отношение Условия передаточного отношения, соосности и сборки выполняются, если подобранные числа зубьев относятся как:
Подставив заданные значения, получим:
если принять z1=20 (>17), тогда
Проверяем полученные числа зубьев сателлитов по условию соседства:
Более простым методом подбора зубьев является метод сомножителей, при котором подбор зубьев ведется только по двум условиям – передаточному отношению и условию соосности, а проверка по условию сборки и соседства. Рассмотрим сущность этого метода на примере двухрядного планетарного механизма с двумя внешними зацеплениями (рис. 2, г). Из уравнения передаточного отношения Тогда:
где подразумевается, что а пропорционально z1; b~z2, с~z2', d~z3. Чтобы обеспечить условие соосности
Значит, соотношение
Отсюда видно, что числа зубьев должны быть соответственно равны:
где γ; – любое положительное число; оно может быть и не целым, например 0,5, если числа перед γ; будут четными. В любом случае zi>;17.
Пример 2. Подобрать числа зубьев для механизма (см. рис.2 г), передаточное отношение которого
Дробь Принимая, что
Условие соосности При
Чтобы получить С целым числом необходимо иметь (1+3 р) кратным 4. При р =0 этого нет. При р =1 С =3 (целое число). Следовательно, при сборке водило необходимо повернуть на угол
которое выполняется. Условие правильного зацепления (отсутствие подреза при
Пример 3. Подобрать числа зубьев для эвольвентных прямозубых нулевых колес двухрядного механизма с двумя внутренними зацеплениями (см. рис.2 в), если
При разложении дроби Из условия соосности вытекает, что выражение
Тогда при
выполняется при р =1, т. е. при повороте водила на угол
Пример 4. Подобрать числа зубьев для двухрядного механизма со смешанным зацеплением (см. рис. 2, б), если известно, что Для этой схемы выражение передаточного отношения
Чтобы обеспечить
при р =0; сборка будет обеспечена с 3 сателлитами при Условие соседства
Критерии оптимальности При синтезе планетарного зубчатого механизма необходимо учитывать не только условия, определяющие его кинематику, но и дополнительные требования, позволяющие улучшить качество механизма. Условия проектирования работоспособного механизма рассмотрены в разд.4. Соответствующие им решения многовариантны, поэтому из них выбирают оптимальное. Таких решений может быть несколько, в зависимости от выбора оценочных параметров. В качестве критериев оптимальности планетарного механизма могут быть выбраны разные условия. Наиболее распространены три критерия оптимальности. 1. Критерий Г — наибольший радиальный габарит. Для получения этого критерия сравнивают габариты ступеней ГI — зацепления колеса 1 с сателлитом 2 и ГII — колеса 3с сателлитом 2(см. рис.2). При этом для внешнего зацепления в качестве габарита принимают величину d ц.к. + 2 d caт., а для внутреннего зацепления ступени — d внут., где d ц.к., d caт., d внут. — диаметры делительных окружностей центрального колеса, сателлита, колеса внутреннего зацепления соответственно. Наибольший из критериев ГI или ГII принимают за критерий Г, оценивающий габарит редуктора. Отметим, что критерий Г не является фактическим габаритом передачи, поскольку для внешнего зацепления габарит определяется через диаметры окружностей вершин соответствующих колес, а для внутреннего зацепления необходимо учитывать размеры зубчатого венца. Поэтому критерий используется только для сравнения вариантов, поскольку понятно, что механизм с большим значением критерия Г будет иметь и большие размеры. Это наиболее важный критерий, поскольку при прочих равных условиях более компактная передача всегда предпочтительнее. 2. Критерий Σ — сумма чисел зубьев (Σ = z1 + z2 + z2¢ + z3), косвенно определяющий массу редуктора и трудоемкость его изготовления. Заметим, что иногда в качестве критерия Σ выбирают более сложное выражение, учитывающее число сателлитов k и, на наш взгляд, более точно отражающее величину массы редуктора, Σ = z1 + k( z 2 + z2¢) + z3. Заметим также, что критерий Σ никак не учитывает случай, когда разные ступени редуктора имеют разные модули. 3. Критерий некратности — условие отсутствия кратности числа зубьев центральных колес числу сателлитов k. При наличии такой кратности в механизме могут возникать периодические силовые возмущения и, кроме того, износ зубьев в этом случае получается неравномерным. Если таковая кратность отсутствует, то механизм с некратным числом зубьев числу сателлитов будет более динамически работоспособным. Это слабый критерий и один из наиболее трудно достижимых, поскольку в случае передаточных отношений некратных числу сателлитов он конфликтует с условием сборки. Как уже указывалось, при синтезе планетарных редукторов число неизвестных зубьев колес больше числа кинематических условий. Следовательно, задача имеет множество решений. Для поиска оптимальных решений из всех вариантов наборов чисел зубьев z1, z2, z2¢, z3, удовлетворяющих кинематическим условиям, рассчитывают оценочные показатели по критериям Σ и Г. Затем, последовательно сравнивая между собой, например, величины Σ для каждого набора, находят наименьшее значение критерия Σ min. Соответствующий ему набор значений чисел зубьев и сателлитов z1, z2, z2¢, z3, k принимают за параметры оптимального механизма, имеющего при прочих равных условиях наименьшую массу. Аналогично, сравнивая величину критерия Г для разных наборов чисел зубьев, находят наименьшее его значение Гmin. Соответствующий ему набор параметров z1, z2, z2¢, z3 и k является оптимальным вариантом механизма с наименьшим радиальным габаритом при прочих равных условиях.
Библиографический список 1. Теория механизмов и машин / под ред. К.В. Фролова. – М.: Высш. школа, 1998. – 496 с. 2. Теория механизмов / под ред. В.А. Гавриленко. М.: Высш. школа, 1973. – 511 с.: ил. 3. Теория механизмов и машин. Курсовое проектирование: учеб. пособие / под ред. Г.А. Тимофеева и Н.В. Умнова. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2010. – 154 с., [2] с.: ил.
Содержание Введение.......................................................................................................................3 1. Строение планетарных редукторов.......................................................................3 2. Преимущества и недостатки планетарных механизмов......................................4 3. Основные характеристики планетарных механизмов.........................................5 4. Синтез планетарных передач.................................................................................8 5. Критерии оптимальности......................................................................................17 Библиографический список......................................................................................19
|


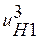 тем больше, чем меньше
тем больше, чем меньше 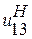 отличается от единицы, где
отличается от единицы, где 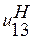 - передаточное отношение преобразованного редуктора при остановленном водиле Н.
- передаточное отношение преобразованного редуктора при остановленном водиле Н.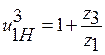
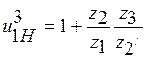
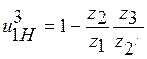
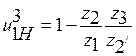
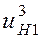 одновременно снижается и к.п.д. При малых значениях
одновременно снижается и к.п.д. При малых значениях 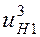 к.п.д. механизма приближается к передаче, составленной из тех же колес с неподвижными осями. Обычно такие механизмы используют при одном сателлите, когда надо получить большие передаточные отношения независимо от к.п.д. (в несиловых передачах). В силовых передачах их применяют только при передаточных отношениях
к.п.д. механизма приближается к передаче, составленной из тех же колес с неподвижными осями. Обычно такие механизмы используют при одном сателлите, когда надо получить большие передаточные отношения независимо от к.п.д. (в несиловых передачах). В силовых передачах их применяют только при передаточных отношениях 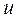 , не превышающих 25. При очень больших значениях передаточных отношений значительно больше проявляется влияние неточности изготовления и сборки на постоянство передаточного отношения в пределах оборота. Поэтому, несмотря на большие кинематические возможности (увеличение передаточных отношений), планетарные механизмы этой группы используют лишь в тех случаях, когда полезные нагрузки невелики. Обычно здесь
, не превышающих 25. При очень больших значениях передаточных отношений значительно больше проявляется влияние неточности изготовления и сборки на постоянство передаточного отношения в пределах оборота. Поэтому, несмотря на большие кинематические возможности (увеличение передаточных отношений), планетарные механизмы этой группы используют лишь в тех случаях, когда полезные нагрузки невелики. Обычно здесь  =25¸35 с тем, чтобы иметь приемлимые к.п.д., а в маломощных передачах
=25¸35 с тем, чтобы иметь приемлимые к.п.д., а в маломощных передачах  достигает 1600.
достигает 1600.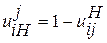 ,
,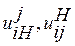 — передаточное отношение от i -го колеса к водилу H при неподвижном j -м колесе и передаточное отношение преобразованного при неподвижном водиле Н соответственно. Передаточное отношение
— передаточное отношение от i -го колеса к водилу H при неподвижном j -м колесе и передаточное отношение преобразованного при неподвижном водиле Н соответственно. Передаточное отношение 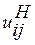 вычисляют с учетом знаков передаточных отношений. Напомним, что внешнее зацепление имеет отрицательное значение передаточного отношения, а внутреннее — положительное.
вычисляют с учетом знаков передаточных отношений. Напомним, что внешнее зацепление имеет отрицательное значение передаточного отношения, а внутреннее — положительное.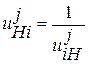
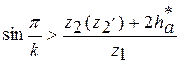 ,
,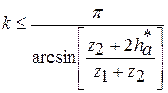
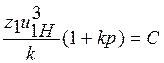 (*),
(*),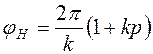 .
.
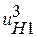 , для проверки условия сборки по соотношению (*) следует подставить передаточное отношение
, для проверки условия сборки по соотношению (*) следует подставить передаточное отношение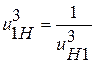 .
. 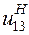
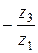
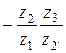
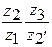
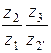
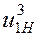
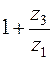
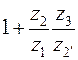
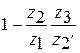
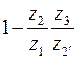

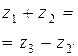
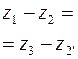

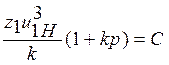

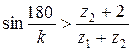
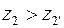
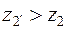
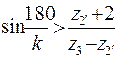
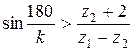
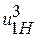 = 5,7 k = 3, все колеса нулевые.
= 5,7 k = 3, все колеса нулевые.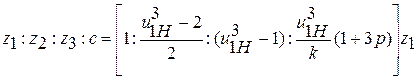
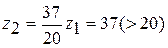
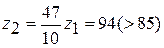 .
.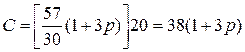 – т. е. число С будет целым даже при p = 0 (угол поворота для установки следующего сателлита 120°).
– т. е. число С будет целым даже при p = 0 (угол поворота для установки следующего сателлита 120°).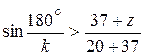 ;
; 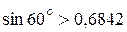
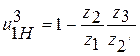 находим значение дроби
находим значение дроби 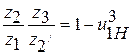 . Отношение
. Отношение 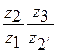 заменяем отношением сомножителей
заменяем отношением сомножителей 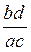 , каждый из которых соответственно должен быть пропорционален числу зубьев.
, каждый из которых соответственно должен быть пропорционален числу зубьев.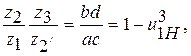
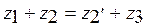 , когда колеса одного модуля, необходимо ввести множители е1и е2,
, когда колеса одного модуля, необходимо ввести множители е1и е2, 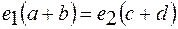 . Проще всего принять в качестве дополнительных множителей
. Проще всего принять в качестве дополнительных множителей 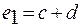 и
и 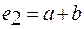 . Тогда условие соосности принимает вид:
. Тогда условие соосности принимает вид: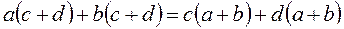 .
.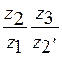 должно быть равно:
должно быть равно: .
.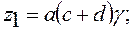
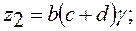

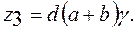
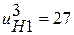 , а число сателлитов k =3. Подстановка значений в равенство
, а число сателлитов k =3. Подстановка значений в равенство 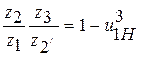 дает:
дает: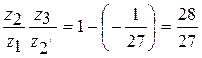
 представляем в виде простых сомножителей
представляем в виде простых сомножителей 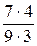 . Таких вариантов решений может быть много, а отсюда и вариантов решений (т. е. вариантов подбора
. Таких вариантов решений может быть много, а отсюда и вариантов решений (т. е. вариантов подбора 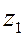 ,
, 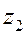 ,
, 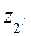 ,
,  ) тоже много.
) тоже много.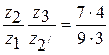 заменим эти цифры равновеликой дробью
заменим эти цифры равновеликой дробью 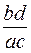 и ищем решение согласно полученным равенствам в виде:
и ищем решение согласно полученным равенствам в виде: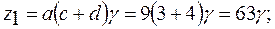
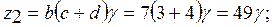
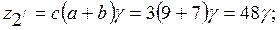
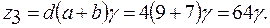
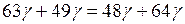 выполняется.
выполняется.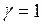
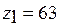 ,
, 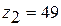 ,
,  ,
, 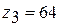 . Проверяем условие сборки по формуле:
. Проверяем условие сборки по формуле: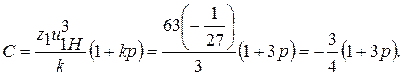
 , т. е. на угол 120о плюс один полный оборот, и тогда будет обеспечена сборка механизма с тремя равномерно распределенными относительно центральных колес сателлитами. Проверим условие соседства
, т. е. на угол 120о плюс один полный оборот, и тогда будет обеспечена сборка механизма с тремя равномерно распределенными относительно центральных колес сателлитами. Проверим условие соседства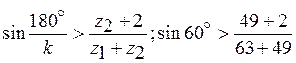 ,
, 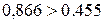
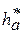 =1,0) также выполнены, так как zi > 17. Таким образом, все условия выполнены.
=1,0) также выполнены, так как zi > 17. Таким образом, все условия выполнены. ; k =3;
; k =3; 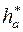 =1,0. Причем
=1,0. Причем  >
> 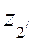 ;
; 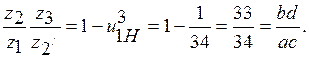
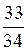 можно получить
можно получить 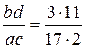 .
.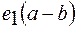 должно равняться
должно равняться 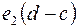 , т. е.
, т. е. 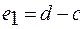 и
и 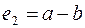 . Числа зубьев колес определятся следующим образом
. Числа зубьев колес определятся следующим образом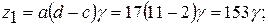
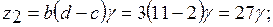
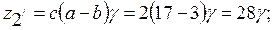
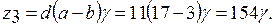
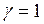
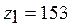 ,
,  ,
, 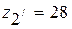 ,
, 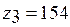 . Проверяем условие сборки
. Проверяем условие сборки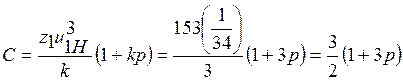
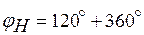 . Условие соседства
. Условие соседства 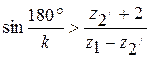 , или
, или  также выполняется. Условия правильного зацепления: число зубьев у колес с внутренними зубьями при
также выполняется. Условия правильного зацепления: число зубьев у колес с внутренними зубьями при 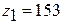 и
и 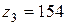 больше 85; разности чисел зубьев колес
больше 85; разности чисел зубьев колес 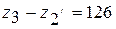 и
и 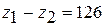 больше 8; число зубьев колес 2 и 2/ больше 20.
больше 8; число зубьев колес 2 и 2/ больше 20. ; k =3;
; k =3; 
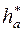 =1,0, колеса нулевые.
=1,0, колеса нулевые. ; условие соосности
; условие соосности 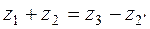 . Причем из схемы следует, что
. Причем из схемы следует, что 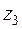 должно быть заведомо больше
должно быть заведомо больше 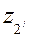 . По передаточному отношению подсчитываем
. По передаточному отношению подсчитываем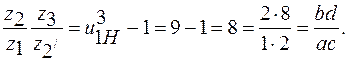 Считая, что а пропорционально
Считая, что а пропорционально 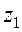 ;
;  ~
~ 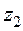 ;
; 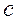 ~
~ 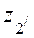 ;
; 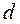 ~
~ 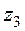 , ищем решение в виде:
, ищем решение в виде: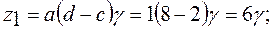
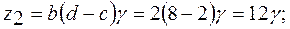
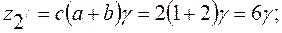
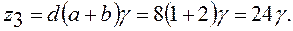
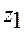 >17, берем γ = 4. Тогда
>17, берем γ = 4. Тогда 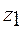 =24,
=24, 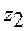 =48,
=48, 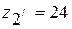 ,
, 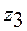 =96. Проверяем условие сборки по формуле:
=96. Проверяем условие сборки по формуле: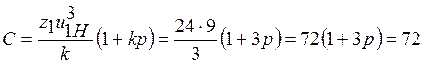
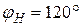 .
. , или
, или 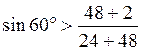 также выполняется. Условия правильного зацепления: число зубьев у колес с внутренними зубьями
также выполняется. Условия правильного зацепления: число зубьев у колес с внутренними зубьями 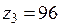 (больше 85); разности чисел зубьев колес
(больше 85); разности чисел зубьев колес 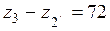 (больше 8); число зубьев колес
(больше 8); число зубьев колес  (больше 17);
(больше 17); 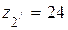 (больше 20).
(больше 20).


