Интерференция света, отраженного от прозрачных пленок
Рассмотрим интерференционные явления, возникающие при отражении света от тонких прозрачных пластин (пленок).
Слагаемое λ/2 появляется в связи с тем, что луч 2´ отражается (в точке С) от оптически более плотной среды, его фаза изменяется на π, что соответствует дополнительной разности хода λ/2. Луч 1´ отражается (в точке В) от оптически менее плотной среды, его фаза не изменяется. Если разность хода равна целому числу длин волн λ падающего света, то лучи 1´ и 2´ максимально усилят друг друга. Нетрудно усмотреть, что при (при данном значении α) такой результат интерференции будет иметь место не только для точки С, но и для всех других точек поверхности пленки. Поэтому глазу, аккомодированному на поверхность пленки, вся пленка представится ярко освещенной. Если же
До сих пор мы имели дело с плоскопараллельной пленкой. Рассмотрим теперь пленку переменной толщины, например, клинообразную (рис.5). В отраженном свете поверхность такой пленки уже не покажется равномерно освещенной, так как разность хода лучей, интерферирующих в различных (по толщине) местах пленки, будет неодинаковой. Эта разность сохраняется постоянной только вдоль линий, параллельных ребру клина, и убывает в направлении от основания к ребру (рис.5 а). Поэтому поверхность клинообразной пленки представится покрытой чередующимися светлыми и темными полосами, параллельными ребру клина (рис.5 б). Очевидно, что чем больше угол клина θ, тем быстрее изменяется разность хода лучей вдоль клина и тем чаще расположены интерференционные полосы. При использовании белого света интерференционные полосы несколько расширяются, приобретая радужную окраску. Это объясняется зависимостью разности хода от длины волны: в каждой светлой полосе максимумы для различных длин волн располагаются раздельно. В отличие от клинообразной пленки у пленки со случайным распределением толщины интерференционные полосы могут иметь самую разнообразную криволинейную форму. При освещении этой пленки белым светом возникает весьма причудливая по форме и расцветке интерференционная картина. Такую картину дают мыльные пленки, нефтяные пятна на поверхности воды, крылья мелких насекомых, жировые налеты на стекле и другие тонкие пленки толщиной порядка 10-4 см. В более толстых пленках цветные интерференционные полосы оказываются настолько сближенными, что частично перекрывают друг друга и интерференционная картина становится неразличимой. Поэтому интерференцию света в толстых пленках можно наблюдать только при использовании строгого монохроматического света.
Рассмотрим систему, состоящую из плосковыпуклой линзы, которая соприкасается своей выпуклой частью с плоской поверхностью хорошо отполированной пластинки (рис.6). Толщина образованной между ними воздушной прослойки растет от центра к краю. Если теперь на эту систему падает пучок монохроматического света, то световые волны, отраженные от нижней поверхности линзы и верхней поверхности пластинки, будут интерферировать между собой в точке C. При этом в центре будет наблюдаться темное пятно, окруженное рядом концентрических, светлых и черных колец убывающей ширины. При наблюдении в проходящем свете будет обратная картина: в центре будет светлое пятно, все светлые кольца заменятся на светлые, и наоборот. Оптическая разность хода лучей в отраженном свете запишется следующим образом: D у = 2 d n + l/2, (9) Один луч сразу отражается в точке В и его фаза не меняется, так как отражение происходит от воздуха в стекло (от оптически менее плотной среды в более плотную), а второй луч дважды проходит воздушную прослойку толщиной d и отражается от стекла в воздух (от оптически более плотной среды в менее плотную). Поэтому фаза луча меняется на p, что соответствует дополнительной разности хода l/2. Так как показатель преломления воздуха n = 1, то формула (9) запишется: Dу = 2 d + l/2, Если в этой разности хода лучей укладывается нечетное число длин полуволн, то при интерференции будет наблюдаться минимум, т.е. условие образования темных колец можно записать как: 2 d + l/2 = (2 к + 1) l/2, или: 2 d = кl, (10) где к = 0, 1, 2, 3, ….является номером темного интерференционного кольца. Толщина воздушной прослойки d может быть выражена через радиус R кривизны линзы и радиус rк темного интерференционного кольца с номером к: rк2 = R2 –(R –d)2. Если d мало по сравнению с R, то rк2» 2 Rd (11) Сравнивая (10) и (11), получим: l = rк2/Rк (12) Однако формула (12) не может быть применена для опытной проверки. Действительно, поскольку на поверхности даже очищенного стекла всегда присутствуют пылинки, то стеклянная линза не примыкает плотно к плоскопараллельной пластинке, а между ними имеется незначительный зазор величиной а. Вследствие зазора возникает дополнительная разность хода в 2 а. Тогда условие образования темных колец примет вид: 2 d + l/2 + 2а = (2 к + 1) l/2, или d = к l/2 – а. Подставляя значение d в уравнение (11),получим: rк2» 2 R к l/2 – 2 R а (13) Величина а не может быть измерена непосредственно, но ее можно исключить следующим образом. Запишем (13) для кольца с номером m: rm2» 2 R m l/2 – 2 R а (14). Вычитая из выражения (14) выражение (13), получим: rm2 – rк2 = R(m – к)l. Откуда
Таким образом, зная радиус кривизны линзы и радиусы rm и rk темных интерференционных колец, можно вычислить длину световой волны l. Выполнение работы На столике микроскопа находятся плосковыпуклая линза и плоскопараллельная пластинка, заключенные в оправу. Включить трансформатор осветителя. С помощью регулятора напряжения и диафрагмы добиться равномерного освещения поля зрения. Затем микроскоп фокусируется на четкое изображение колец. Оправа с линзой и стеклом устанавливается так, чтобы крест нитей окулярного микрометра проходил через центр колец. Когда кольца Ньютона в увеличенном виде будут хорошо видны, оправу с линзой и стеклом смещают, чтобы можно было наблюдать максимальное число колец с одной стороны (рис.7). Вращая барабан окулярного микрометра, наводят крест нитей на центр темного пятна и производят отсчет (не менее пяти раз) целых делений по положению двух штрихов на шкале и сотых по барабану. Положение центра колец определяется как среднее арифметическое этих отсчетов. Затем наводят крест нитей на первое, второе и т.д. (до последнего видимого в окуляр) кольцо и определяют один раз положение каждого кольца. Радиусы колец определяются как разности положений колец и центра. Примечание. Необходимо помнить, что одно целое деление шкалы в микроскопе, соответствующее одному полному обороту барабана окуляр-микрометра, содержит 100 делений барабана. Для данного микроскопа с учетом увеличения объектива и окулярного микрометра цена одного деления шкалы барабана равна 0,0008 мм.
Для повышения точности результатов определения длины волны света l рекомендуется комбинировать радиус кольца rm и радиусом кольца rk. Если m – четный номер кольца, то k=m/ 2. Если m – нечетный номер кольца, то k=(m-1)/ 2. Например, если m =12, то k =6; если m =11, то k =5. Для красного светофильтра необходимо измерить не менее 12 – 15 колец. Для синего и зеленого и желтого светофильтров число хорошо видимых колец меньше. По формуле (15) определяют длину волны света, пропускаемого данным светофильтром. Для каждого светофильтра рассчитывают длину волны не менее трех раз, комбинируя разными значениями m и k. Примечание. Так как ширина колец вблизи центра интерференционной картины наибольшая, то расчет длины волны следует проводить по значениям радиусов колец, наиболее удаленных от центра. Радиус кривизны линзы R=14,4 мм. Результаты измерений заносят в таблицу.
Контрольные вопросы 1. Дайте определение явлению интерференция света. 2. Какие волны называются когерентными? 3. В чем состоит условие максимума и минимума света при интерференции? 4. Из чего складывается полная оптическая разность хода? 5. В каких случаях изменяется разность хода лучей на l/2 при отражении? 6. Объясните физическую сущность образования колец Ньютона. РАБОТА № 6(9) ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ ПРИ ПОМОЩИ ДИФРАКЦИОННОЙ РЕШЕТКИ
Приборы и принадлежности: гониометр, плоская дифракционная решетка, осветительсо светофильтрами.
|

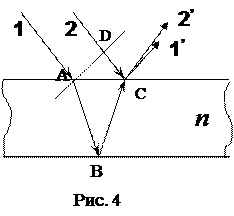 Пусть на тонкую пленку толщиной d падают параллельные лучи монохроматического света (рис.4). Очевидно, что из некоторой точки С будут выходить два практически совпадающих когерентных луча: луч 2´, отраженный от верхней поверхности пленки, и луч 1´, отраженный от нижней ее поверхности. Понятно, что разность хода
Пусть на тонкую пленку толщиной d падают параллельные лучи монохроматического света (рис.4). Очевидно, что из некоторой точки С будут выходить два практически совпадающих когерентных луча: луч 2´, отраженный от верхней поверхности пленки, и луч 1´, отраженный от нижней ее поверхности. Понятно, что разность хода 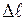 этих лучей зависит от угла падения α и толщины пленки d пленки. Кроме того,
этих лучей зависит от угла падения α и толщины пленки d пленки. Кроме того, 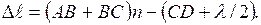 (8)
(8)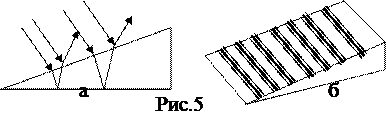 Таким образом, изменяя угол падения α, мы увидим пленку попеременно то светлой, то темной.
Таким образом, изменяя угол падения α, мы увидим пленку попеременно то светлой, то темной.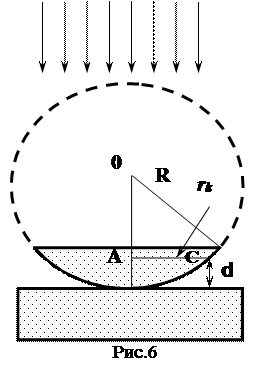 Кольца Ньютона
Кольца Ньютона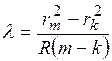 . (15)
. (15) Если, например, число целых делений равно 2, число сотых делений – 15, то отсчет составляет 215 единиц.
Если, например, число целых делений равно 2, число сотых делений – 15, то отсчет составляет 215 единиц.


