Краткая теория. Явление дифракции света состоит в отклонении световой волны от прямолинейного распространения
Явление дифракции света состоит в отклонении световой волны от прямолинейного распространения. Дифракция происходит, когда световые лучи встречают на своём пути какое-либо препятствие, но особенно отчетливо она обнаруживается в тех случаях, когда размеры огибаемых непрозрачных экранов или отверстий, через которые проходят лучи, настолько малы, что являются соизмеряемыми с длиной световой волны.
Дифракционная картина возникает в результате наложения (интерференции) вторичных волн, поэтому ей присущи типичные для интерференции черты - неравномерное распределение энергии в пространстве. В одних местах интенсивность света - больше, в других меньше. Таким образом, в подвергшейся дифракции световой волне по отношению к падающей происходит перераспределение интенсивности света.
Рассмотрим волны, которые распространяются от плоскости AB в направлении, составляющим с первоначальным, некоторый угол j. Если на пути этих лучей поставить линзу, параллельную плоскости AB, то, как показано на рисунке 1, эти параллельные лучи после преломления сойдутся в некоторой точке М в фокальной плоскости линзы. Располагая в этой фокальной плоскости экран Е, можно на нем наблюдать результат интерференции для волн, распространяющихся от щели под различными произвольными углами j к первоначальному направлению. Опустим из точки А перпендикуляр АС на направление выделенного пучка лучей, который будет нормально пересекаться плоскостью, проходящей через этот перпендикуляр. Тогда от плоскости АС и далее до фокальной плоскости Е параллельные лучи не меняют своей разности хода. Разность хода, определяющая условия интерференции, возникает лишь на пути от исходного фронта AB до плоскости, AC и различна для разных лучей. Для расчета интерференции всех этих лучей применим метод зон Френеля (зонами Френеля называются зоны волновой поверхности, обладающие тем свойством, что разность хода световых лучей от двух соответственных точек соседних зон равна половине длины световой волны Из приведенного построения следует, что волны, идущие от каждых двух соседних зон Френеля, приходят в точку М в противоположной фазе и гасят друг друга. Разность хода D между крайними лучами, т.е. лучами, исходящими из точек А и B, будет, как видноиз рис.1.а, равна
Если выбрать угол дифракции j таким, чтобы в ширине щели укладывалось четное число зон Френеля, то, очевидно,
где k - целое число, не равное нулю. В этом случае все лучи, идущие в направлении, определяемом углом j, после сведения их линзой в одну точку экрана будут взаимно уничтожаться. Действительно, для каждого луча любой зоны существует луч в соседней зоне, который находится с ним в противофазе. Следовательно, любые два симметричные луча от двух соседних зон будут взаимно уничтожаться, т.е., одна зона будет гасить другую, соседнюю с ней. Таким образом, условие (2) определяет положение на экране темных полос - минимумов света. Если же угол дифракции выбрать таким, что в щели будет укладываться нечетное число зон Френеля, то, очевидно,
В этом случае одна зона не будет иметь парной себе, которая уничтожила бы ее действие, и лучи в этом направлении дадут максимум освещенности. Таким образом, условие (3) определяет положение на экране светлой полосы - максимума света. (На рис.1 в щели укладываются три зоны Френеля.) Ясно, что при непрерывном изменении угла j мы последовательно будем наблюдать темные и светлые полосы. Центральный максимум будет расположен в точке 0 против центра щели. По обе стороны от него интенсивность будет спадать до первого минимума, а затем подыматься до следующего максимума и т.д., как это показано на рис.1.б. На экране Е будут наблюдаться, как это показано на рис.1.в, перемежающиеся светлые и темные полосы с постепенными переходами между ними. Центральная полоса будет наиболее яркой, а освещенность боковых максимумов будет убывать от центра к периферии. Ширина и число этих полос будут зависеть от отношения длины световой волны l к ширине щели a. Совокупность большого числа узких параллельных щелей, расположенных близко друг от друга, называется дифракционной решеткой.
Пусть свет с длиной волны l падает нормально на дифракционную решетку (рис.2). За щелями в результате дифракции лучи будут распространяться по различным направлениям. Рассмотрим лучи, составляющие угол j с нормалью к дифракционной решетке. Разность хода лучей, проходящих через левые края первой и второй щелей, равна
Сумма a+b=d называется периодом или постоянной дифракционной решетки. Этой разности хода BC, соответствует разность фаз между лучами δ;
Такойже точно сдвиг фазы будет между колебаниями, приходящими от третьей щели и второй, четвертой и третьей, и т.д. Если D=l, то d=2p. Эти лучи приходят в одинаковых фазах и усиливают друг друга. Резкое возрастание амплитуды результирующего колебания будет в тех случаях, когда амплитуды колебаний от всех направлений одинаковы, т.е. имеют сдвиг фаз, целый кратный от 2p, что соответствует разности хода d между соседними щелями, кратной четному числу полуволн. Таким образом, условием образования максимумов будет формула
где п = 0, ±1, ±2, ±3, Максимумы, удовлетворяющие этому условию, называются главными максимумами дифракционной решетки. Интересно отметить, что если при дифракции от одной щели условие максимумов (3) соответствует нечётному числу зон Френеля внутри щели, то длявсейрешетки в целом условие главных максимумов (6)соответствует разности хода от разных щелей, равной четному числу полуволн.
Согласно формуле (6), по обе стороны от центрального максимума, которому соответствует значение n = 0, располагаются первые максимумы - правый (n = +1) и левый (n = -1), далее располагаются вторые максимумы (n = +2 и n = -2) и т.д. Однако возможное число максимумов является ограниченным; оно не может быть больше, чем Если на дифракционную решетку будет падать белый свет, то дифракционные максимумы для лучей разного цвета пространственно разойдутся и каждый максимум (кроме центрального) приобретает радужную окраску, причем внутренний его край (по отношению к центральному максимуму) станет фиолетовым, а наружный - красным, так как фиолетовому цвету соответствуют наиболее короткие волны, а красному -наиболее длинные. Между фиолетовым и красным краями максимума расположатся остальные спектральные цвета. В этой связи дифракционные максимумы принято называть дифракционными спектрами, а число n - порядком спектра. Максимум нулевого порядка остается белым, таккак,согласно формуле (6), при n = 0 угол дифракции j = 0 для всех длин волн l.
|

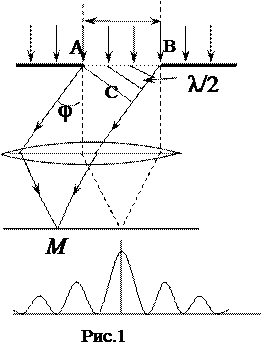 При использовании белого света дифракционная картина приобретает радужную окраску.
При использовании белого света дифракционная картина приобретает радужную окраску. ). Для этого мысленно разделим линию ВС на ряд отрезков длиною
). Для этого мысленно разделим линию ВС на ряд отрезков длиною  (1)
(1) , (2)
, (2)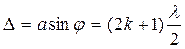 (3)
(3) Рассмотрим ряд щелей одинаковой шириныa, расположенныхнаравных расстояниях b друг от друга. При прохождении света через систему таких одинаковых щелей дифракционная картина значительно усложняется. В этом случае дифрагирующие лучи от отдельных щелей налагаются друг на друга в фокальной плоскости линзы и интерферируют между собой.
Рассмотрим ряд щелей одинаковой шириныa, расположенныхнаравных расстояниях b друг от друга. При прохождении света через систему таких одинаковых щелей дифракционная картина значительно усложняется. В этом случае дифрагирующие лучи от отдельных щелей налагаются друг на друга в фокальной плоскости линзы и интерферируют между собой.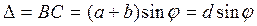 (4)
(4) (5)
(5)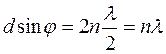 , (6)
, (6) На рис.3 показана дифракционная картина, получающаяся при сложении колебаний от нескольких щелей.
На рис.3 показана дифракционная картина, получающаяся при сложении колебаний от нескольких щелей.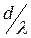 . В самом деле, согласно формуле (6),
. В самом деле, согласно формуле (6), 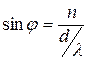 ,но
,но 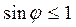 , следовательно,
, следовательно,  . Чем больше постоянная решетки d,тем большее число максимумов можно наблюдать и более узкими становятся отдельные полосы.
. Чем больше постоянная решетки d,тем большее число максимумов можно наблюдать и более узкими становятся отдельные полосы.


