С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА
Приборы и принадлежности: плоскопараллельная стеклянная пластинка и плосковыпуклая линза в оправе, микроскоп с осветителем отраженного света, окулярный микрометр, набор светофильтров. Уравнение волны
График волны (рис.1) внешне похож на график гармонического колебания, но по существу они различны. График колебания представляет зависимость смещения частицы от времени, график волны – смещения всех частиц среды относительно положения равновесия в зависимости от ее расстояния до источника колебаний в данный момент времени. Он является как бы моментальной фотографией волны. Рассмотрим некоторую частицу С, находящуюся на расстоянии у от источника колебаний (частицы О). Очевидно, что если частица О колеблется уже t секунд, то частица С колеблется еще только (t -τ) секунд, где τ – время распространения колебаний от 0 до С, т.е. время, за которое волна переместилась на определенное расстояние у. Тогда уравнение колебания частицы С следует написать так:
Но
Соотношение (1), позволяющее определить смещение (отклонение) любой точки среды от положения равновесия в любой момент времени, называется уравнением волны. Вводя в рассмотрение длину волны λ как расстояние между двумя ближайшими точками волны, находящимися в одинаковой фазе, например, между двумя соседними гребнями волны, можно придать уравнению волны другой вид. Очевидно, что длина волны равна расстоянию, на которое распространяется колебание за период Т со скоростью v:
где ν – частота волны. Тогда, подставляя в уравнение (1)
или Интерференция волн Если в среде несколько источников колебаний, то исходящие от них волны распространяются независимо друг от друга и после взаимного пересечения расходятся, не имея никаких следов происшедшей встречи. Это положение называется принципом суперпозиции. Его иллюстрацией может служить распространение водяных волн, вызванных двумя брошенными на поверхность воды камнями (рис.2).
В местах встречи волн колебания среды, вызванные каждой из волн, складываются друг с другом (можно сказать: волны складываются) Результат сложения (результирующая волна) зависит от соотношения фаз, периодов и амплитуд встречающихся волн. Большой практический интерес представляет случай сложения двух (или нескольких) волн, имеющих постоянную разность фаз и одинаковые частоты. Подразумевается, что направление колебаний у всех волн одинаково. Такие волны и создающие их источники колебаний называются когерентными. Сложение когерентных волн называется интерференцией. Рассмотрим интерференцию двух волн одинаковой амплитуды, исходящих из Согласно уравнению волны (3), смещения, вызванные в точке Р первой и второй волнами, равны соответственно: х1 = А sin(ωt –2πу1/λ) и х2 = А sin(ωt –2πу2/λ) В результате точка Р будет совершать колебания по синусоидальному закону: х = х1+х2 = 2А cos 2π(у1 –y2) /λ ·sin(ωt –2π(у1 +y2 ) /λ) с амплитудой 2А cos 2π(у1 –y2) /λ, зависящей отразности фаз
Если то в точке Р наблюдается максимум: колебания максимально усилят друг друга и результирующая амплитуда будет равна 2 А. Если же где n =0,1,2,3,…, то в точке Р будет минимум: колебания взаимно погасятся и результирующая амплитуда в этом случае равна нулю. Условия максимума (4) и минимума (5) можно еще записать соответственно так:
где Δ у= (у1 –y2) – разность хода волн, или разность хода лучей. Следовательно, в точке Р будет максимум, если разность хода волн составляет четное число полуволн (целое число волн); если разность хода составляет нечетное число полуволн, то в точке Р будет минимум. Так как волны распространяются от источников S΄ и S˝ по всем направлениям, то в пространстве окажется множество точек, удовлетворяющих как условию (6), так и условию (7), т.е. найдется множество точке, соответствующих максимуму и минимуму колебаний. Поэтому интерференционная картина представит собой чередование областей усиления колебаний (максимумов) и областей, где колебания отсутствуют (минимумов). Более подробно эта интерференционная картина будет рассмотрена ниже для случая электромагнитных световых волн.
|

 Установим зависимость между смещением х частиц среды, участвующих в волновом процессе, и расстоянием у этих частиц от источника О колебаний для любого момента времени t. Для большей наглядности рассмотрим поперечную волну, хотя все последующие рассуждения верны и для продольной волны. Пусть колебания источника (точка О) являются гармоническими:
Установим зависимость между смещением х частиц среды, участвующих в волновом процессе, и расстоянием у этих частиц от источника О колебаний для любого момента времени t. Для большей наглядности рассмотрим поперечную волну, хотя все последующие рассуждения верны и для продольной волны. Пусть колебания источника (точка О) являются гармоническими: 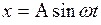 , где А – амплитуда, ω – круговая частота колебаний. Тогда все частицы среды тоже придут в гармоническое колебание с той же частотой и амплитудой, но с различными фазами. В среде возникает синусоидальная волна (рис.1).
, где А – амплитуда, ω – круговая частота колебаний. Тогда все частицы среды тоже придут в гармоническое колебание с той же частотой и амплитудой, но с различными фазами. В среде возникает синусоидальная волна (рис.1).
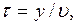 где v – скорость распространения волны. Тогда
где v – скорость распространения волны. Тогда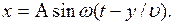 (1)
(1) (2)
(2)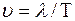 и учитывая, что
и учитывая, что 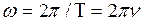 , получим другие формы уравнения волны:
, получим другие формы уравнения волны:
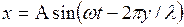 . (3)
. (3)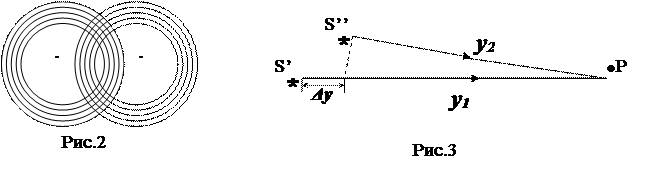
 когерентных источников S΄ и S˝ и встречающихся в точке Р (рис.3).
когерентных источников S΄ и S˝ и встречающихся в точке Р (рис.3). .
.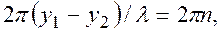 (4)
(4)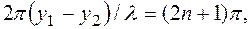 (5)
(5) (6)
(6)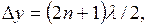 (7)
(7)


