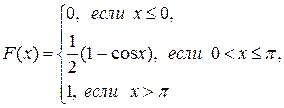4 страница. 8. Стрелок произвел 4 выстрела с вероятностью поражения цели при отдельном выстреле 0,7
8. Стрелок произвел 4 выстрела с вероятностью поражения цели при отдельном выстреле 0,7. Составить ряд распределения случайной величины Х -числа поражений цели. Определить вероятность того, что среди 4 выстрелов цель будет поражена: а) ровно четыре раза; б) более четырех раз; в) не более четырех раз. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Средний размер стволов берез на некотором участке равен 25см, среднее квадратическое отклонение равно 5см. Считая диаметр ствола березы случайной величиной, распределенной нормально, найти процент деревьев, имеющих диаметр свыше 20см. Вариант №28 1. Вероятности того, что нужная сборщику деталь находится в первом, втором, третьем и четвёртом ящике соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятность того, что деталь содержится: а) хотя бы в одном ящике; б) не менее чем в двух ящиках. 2. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 6. 3. В урне 10 шаров, из них 7 – окрашенные. Найти вероятность того, что ровно 2 из 3-х вынутых наудачу шаров окрашены. 4. В телевизионном ателье 4 кинескопа. Вероятности того, что кинескоп выдержит гарантийный срок службы, соответственно равны 0,8; 0,85; 0,9; 0,95. А) Найти вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок службы. В) Кинескоп выдержал гарантированный срок использования. Какова вероятность того, что это был кинескоп №1? 5. Вероятность появления события в каждом из 300 независимых испытаний равна 0,25. Найти вероятность того, что в этих испытаниях интересующее событие наступит ровно 240 раз? 6. Рабочий за смену изготавливает 400 деталей. Вероятность того, что деталь окажется первого сорта, равна 0,9. Какова вероятность того, что деталей первого сорта будет от 355 до 382 штук? 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-2Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Составить ряд распределения случайной величины Х -числа включенных моторов. Определить вероятность того, что в данный момент: а) включено четыре мотора; б) более четырех моторов; в) не более четырех моторов. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Процент всхожести семян свеклы равен 90%. Оценить вероятность того, что из 1000 посеянных семян взойдет от 850 до 950 семян включительно. Вариант №29 1. В студии телевидения три телевизионных камеры. Для каждой камеры вероятность того, что она включена в данный момент, равна 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера, не менее двух камеры. 2. В круг радиуса 8 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 5. 3. В урне 12 шаров, из них 8 – окрашенные. Найти вероятность того, что ровно 2 из 4-х вынутых наудачу шаров окрашены. 4. В двух ящиках имеются радиолампы. В первом ящике содержится 12 ламп, из них 1 нестандартная; во втором 10 ламп, из них 1 нестандартная. Из первого ящика наудачу взята лампа и переложена во второй. Найти вероятность того, что наудачу извлечённая из второго ящика лампа будет нестандартна. 5. Вероятность появления события в каждом из 600 независимых испытаний равна 0,4. Найти вероятность того, что в этих испытаниях интересующее событие наступит ровно 375 раз? 6. Рабочий за смену изготавливает 600 деталей. Вероятность того, что деталь окажется первого сорта, равна 0,6. Какова вероятность того, что деталей первого сорта будет от 210 до 252 штук? 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-2Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Вероятность того, что событие A появится в одном из пяти независимых испытаниях, равна 0,3. Составить ряд распределения случайной величины Х -числа появлений события А. Определить вероятность того, что среди 5 испытаний событие появится: а) ровно два раза; б) более двух раз; в) не более двух раз. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал (0,2;0,9); в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:
Построить графики функции и плотности распределения случайной величины Х. 10. Пусть вес пойманной рыбы подчиняется нормальному закону с параметрами a =375г и σ=25г. Найдите вероятность того, что вес пойманной рыбы будет от 300 до 425г. Вариант №30 1. Имеется 4 машины. Вероятность того, что машина работает в произвольный момент времени t, равна 0,9. Найти вероятность того, что в момент t работает: а) не более двух машин; б) две машины; в) хотя бы одна машина. 2. В круг радиуса 6 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 4. 3. В урне 12 шаров, из них 6 – окрашенные. Найти вероятность того, что ровно 2 из 3-х вынутых наудачу шаров окрашены. 4. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4, из второй-6, из третьей-5 студентов. Вероятность того, что студент первой, второй, третьей группы попадёт в сборную института, соответственно равны 0,9; 0,7 и 0,8. Наудачу выбирается студент одной из групп. А) Какова вероятность того, что он попадет в сборную? В) В итоге соревнования студент попал в сборную. Найти вероятность того, что он принадлежал первой группе. 5. Вероятность появления события в каждом из 625 независимых испытаний равна 0,36. Найти вероятность того, что в этих испытаниях интересующее событие наступит ровно 370 раз? 6. Рабочий за смену изготавливает 625 деталей. Вероятность того, что деталь окажется первого сорта, равна 0,64. Какова вероятность того, что деталей первого сорта будет от 225 до 255 штук? 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-2Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Вероятность выигрыша по одному билету лотереи 0,2. Приобретено 5 билетов. Составить ряд распределения случайной величины Х -числа выигрышей по билету в лотереи. Определить вероятность того, что среди 5 приобретенных билетов выигрышных: а) ровно четыре билета; б) более четырех билетов; в) не более четырех билетов. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Случайная величина Х распределена по нормальному закону с математическим ожиданием, равным 40, и дисперсией, равной 200. Вычислить вероятность попадания случайной величины в интервал (30; 80).
|

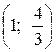 ; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:
; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:
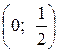 ; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:
; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X: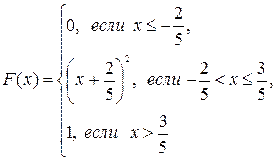
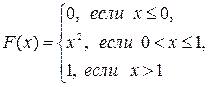
 ; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:
; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X: