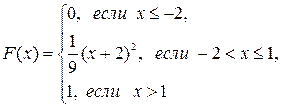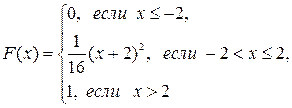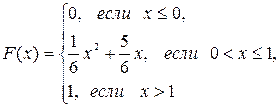1 страница. 1. Три стрелка производят по одному выстрелу в цель независимо друг от друга
Вариант №1 1. Три стрелка производят по одному выстрелу в цель независимо друг от друга. Вероятности попадания в цель для каждого из них соответственно равны 0,7; 0,8; 0,9. Найти вероятность того, что: а) в цель попадает только один стрелок; б) в цель попадают только два стрелка; в) в цель попадает хотя бы один стрелок. 2. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 5. 3. В урне 10 шаров, из них 6 – окрашенные. Найти вероятность того, что ровно 2 из 3-х вынутых наудачу шаров окрашены. 4. На одном заводе на каждые 100 лампочек приходится в среднем 10 нестандартных, на втором – 15, а на третьем – 20. Продукция этих заводов составляет 50; 30 и 20% всех электролампочек, приобретаемых жителями района. А) Найти вероятность того, что приобретенная лампочка будет стандартной. В) Приобретенная лампочка оказалась стандартной. Какова вероятность того, что эта лампочка изготовлена на первом заводе? 5. Рабочий за смену изготавливает 400 деталей. Вероятность того, что деталь окажется первого сорта, равна 0,8. Какова вероятность того, что деталей первого сорта будет ровно 330 штук? 6. Вероятность появления события А в каждом из 150 независимых испытаний равна 0,6. Найти вероятность того, что в этих испытаниях событие А появится от 78 до 96 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-2Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Составить ряд распределения случайной величины Х -числа бракованных деталей в выборке объема п =4. Вероятность того, что деталь окажется бракованной, равна 0,8. Определить вероятность того, что в выборке будет бракованных: а) ровно две детали; б) более двух деталей; в) не более двух деталей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) вероятность попадания случайной величины X в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 200мм, среднее квадратическое отклонение равно 0,25мм. Стандартными считаются детали, размер которых заключен между 199,5мм и 200,5мм. Найти процент стандартных деталей. Вариант №2 1. Вероятность выполнения плана бригадами соответственно равна 0,8 и 0,9. Найти вероятность того, что выполнят план: а) обе бригады; б) хотя бы одна бригада; в) только одна бригада. 2. В круг радиуса 9 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 4. 3. В лотерее 10 билетов, из которых 4 выигрышных. Какова вероятность, что выиграют два билета при покупке четырех билетов. 4. Всхожесть семян свеклы первой партии 90%, второй партии-80%. Перед посевом смешали 2ц семян первой партии и 3ц семян второй партии. А) Какова вероятность всхода, если посадили одно семя? В) Семя взошло. Какова вероятность того, что оно из первой партии? 5. Вероятность попадания в цель при одном выстреле составляет 0,8. Найти вероятность 165 попаданий при 225 выстрелах. 6. Вероятность появления события А в каждом из 100 независимых испытаний равна 0,8. Найти вероятность того, что в этих испытаниях событие А появится от 72 до 84 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-2Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Составить ряд распределения случайной величины Х -числа бракованных деталей в выборке объема п =5. Вероятность того, что деталь окажется бракованной, равна 0,2. Определить вероятность того, что в выборке будет бракованных: а) ровно три детали; б) более трех деталей; в) не более трех деталей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) вероятность попадания случайной величины X в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Средний размер стволов деревьев на некотором участке равен 25см, среднее квадратическое отклонение равно 5см. Считая диаметр ствола случайной величиной, распределенной нормально, найти процент деревьев, имеющих диаметр свыше 20см. Вариант №3 1. Всхожесть семян первого, второго и третьего сорта некоторой культуры составляет соответственно 90%; 80% и 70%. Вычислить вероятность того, что из трех посеянных разносортных семян этой культуры: а) взойдут все три; б) взойдет только одно; в) взойдет хотя бы одно. 2. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 4. 3. В ящике 15 деталей, из них 6 – бракованные. Найти вероятность того, что ровно одна из трех вынутых деталей – бракованная. 4. На фабрике на машинах А, В С производят соответственно 25; 35 и 40% всех изделий. В их продукции брак составляет соответственно 15; 10 и 5%. А) Найти вероятность того, что случайно выбранное изделие окажется дефектным. В) Выбранное изделие оказалось дефектным. Найти вероятность того, что оно изготовлено на машине А. 5. Всхожесть семян оценивается вероятностью 0,75. Какова вероятность того, что из 192 посеянных семян взойдет ровно 150? 6. Вероятность появления события А в каждом из 400 независимых испытаний равна 0,9. Найти вероятность того, что в этих испытаниях событие А появится от 345 до 372 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Составить ряд распределения случайной величины Х -числа бракованных деталей в выборке объема п =6. Вероятность того, что деталь окажется бракованной, равна 0,1. Определить вероятность того, что в выборке будет бракованных: а) ровно четыре детали; б) более четырех деталей; в) не более четырех деталей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) вероятность попадания случайной величины X в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Процент всхожести семян равен 90%. Оценить вероятность того, что из 1000 посеянных семян взойдет от 850 до 950 семян включительно. Вариант №4 1. Для сигнализации об аварии установлены три независимо работающих датчика. Вероятность исправной работы первого датчика равна 0,9; второго – 0,95; третьего – 0,8. Найти вероятность того, что: а) сработает только один датчик; б) сработает только два датчика; в) сработает хотя бы один датчик. 2. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 6. 3. Студент знает 25 из 30 вопросов экзамена. Найти вероятность того, что студент сдаст экзамен, если для этого достаточно ответить на 3 из 5 предложенных экзаменатором вопроса. 4. На спартакиаду прибыло 20 лыжников, 15 гимнастов, 5 шахматистов. Вероятность выполнить квалификационную норму такова: для лыжника – 0,8; для гимнаста – 0,6; для шахматиста – 0,9. Случайно вызывается один спортсмен. А) Какова вероятность того, что он выполнит норму? В) Спортсмен выполнил норму. Какова вероятность того, что это был шахматист? 5. Вероятность того, что семя злака прорастет, равна 0,9. Найти вероятность того, что из 100 семян прорастет ровно 95 семян. 6. Вероятность появления события А в каждом из 600 независимых испытаний равна 0,4. Найти вероятность того, что в этих испытаниях событие А появится от 210 до 252 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-2Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Составить ряд распределения случайной величины Х -числа бракованных деталей в выборке объема п =5. Вероятность того, что деталь окажется бракованной, равна 0,3. Определить вероятность того, что в выборке будет бракованных: а) ровно четыре детали; б) более четырех деталей; в) не более четырех деталей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) вероятность попадания случайной величины X в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Среднее квадратическое отклонение нормально распределенной случайной величины равно 0,5. Найти вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине не превосходит 1. Вариант №5 1. Рабочий обслуживает три станка. Вероятность бесперебойной работы в течение одного месяца для первого станка равна 0,8; для второго – 0,9; для третьего – 0,8. Найти вероятность того, что в течение одного месяца без остановки будут работать: а) все станки; б) только два станка; в) хотя бы один станок. 2. В круг радиуса 8 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 6. 3. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают три изделия для контроля. Найти вероятность события что в полученной выборке одно изделие бракованное. 4. На одном заводе на каждые 100 лампочек приходится в среднем 15 нестандартных, на втором – 10, а на третьем – 25. Продукция этих заводов составляет 30; 45 и 25% всех электролампочек, приобретаемых жителями района. А) Найти вероятность того, что приобретенная лампочка будет стандартной. В) Приобретенная лампочка оказалась стандартной. Какова вероятность того, что эта лампочка изготовлена на первом заводе? 5. Найти приближённо вероятность того, что при 400 испытаниях событие наступит ровно 330 раз, если вероятность его появления в каждом испытании равна 0,8. 6. Вероятность появления события А в каждом из 300 независимых испытаний равна 0,75. Найти вероятность того, что в этих испытаниях событие А появится от 210 до 225 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-2Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Составить ряд распределения случайной величины Х – числа бракованных деталей в выборке объема п =4. Вероятность того, что деталь окажется бракованной, равна 0,8. Определить вероятность того, что в выборке будет бракованных: а) ровно три детали; б) более трех деталей; в) не более трех деталей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) вероятность попадания случайной величины X в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 150мм и средним квадратическим отклонением 0,5мм. Какую точность размера детали можно гарантировать с вероятностью 0,95. Вариант №6 1. Вероятность установления в данной местности устойчивого снежного покрова с октября равна 0,1. Определить вероятность того, что в ближайшие три года в этой местности устойчивый снежный покров с октября: а) не установится ни разу; б) установится хотя бы один раз; в) установится два раза. 2. В круг радиуса 7 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 5. 3. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают три изделия для контроля. Найти вероятность события что в полученной выборке два изделия бракованных. 4. На спартакиаду прибыло 20 спортсменов школы №1, 15 спортсменов школы №2 и 5 спортсменов школы №3. Вероятность выполнить квалификационную норму такова: для школы №1 – 0,8; для школы №2 – 0,6; для школы №3 – 0,9. Случайно вызывается один спортсмен. А) Какова вероятность того, что он выполнит норму? В) Спортсмен выполнил норму. Какова вероятность того, что это был спортсмен из школы №2? 5. Всхожесть семян оценивается вероятностью 0,9. Какова вероятность того, что из 100 посеянных семян взойдет ровно 96? 6. Вероятность появления события А в каждом из 625 независимых испытаний равна 0,36. Найти вероятность того, что в этих испытаниях событие А появится от 225 до 255 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=2X+4Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Составить ряд распределения случайной величины Х -числа бракованных деталей в выборке объема п =3. Вероятность того, что деталь окажется бракованной, равна 0,1. Определить вероятность того, что в выборке будет бракованных: а) ровно две детали; б) более двух деталей; в) не более двух деталей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) вероятность попадания случайной величины X в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Средний вес зерна равен 0,2г, среднее квадратическое отклонение равно 0,05г. Определить вероятность того, что вес наудачу взятого зерна окажется в пределах от 0,16г до 0,22г. Вариант №7 1. Исследователь разыскивает нужные ему сведения в трех справочниках. Вероятности того, что эти сведения находятся в 1-ом, 2-ом, 3-ем справочниках соответственно равны 0,7; 0,6 и 0,9. Найти вероятность того, что требуемые сведения содержаться: а) только в одном справочнике, б) хотя бы в одном справочнике, в) во всех справочниках. 2. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 5. 3. В урне 9 шаров, из них 6 – окрашенные. Найти вероятность того, что ровно 2 из 3-х вынутых наудачу шаров окрашены. 4. Всхожесть семян астры первой партии 80%, второй партии-70%. Перед посевом смешали 3ц семян первой партии и 2ц семян второй партии. А) Какова вероятность всхода, если посадили одно семя? В) Семя взошло. Какова вероятность того, что оно из первой партии? 5. Вероятность попадания в цель при одном выстреле составляет 0,6. Найти вероятность 75 попаданий при 150 выстрелах. 6. Вероятность появления события А в каждом из 400 независимых испытаний равна 0,5. Найти вероятность того, что в этих испытаниях событие А появится от 190 до 215 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Составить ряд распределения случайной величины Х – числа бракованных деталей в выборке объема п =3. Вероятность того, что деталь окажется бракованной, равна 0,7. Определить вероятность того, что в выборке будет бракованных: а) ровно две детали; б) более двух деталей; в) не более двух деталей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) вероятность попадания случайной величины X в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Норма высева семян на 1га равна 200кг. Фактический расход семян на 1га колеблется от этого значения со средним квадратическим отклонением 10кг. Определить количество семян, обеспечивающих посев на площади 100га с гарантией 0,95. Вариант №8 1. Всхожесть фасоли 80%, гороха 90%, бобов 70%. Определить вероятность того, что из трех посеянных семян различных культур: а) взойдут два; б) не взойдет ни одного, в) взойдет хотя бы одно. 2. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 6. 3. В урне 10 шаров, из них 7 – окрашенные. Найти вероятность того, что ровно 2 из 3-х вынутых наудачу шаров окрашены. 4. На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 3% брака, второй – 2%, а третий – 4%. А) Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 1000, со второго – 2000 и с третьего – 2500 деталей. В) деталь оказалась бракованной. Найти вероятность того, что она изготовлена на третьем автомате. 5. Найти приближённо вероятность того, что при 900 испытаниях событие наступит ровно 340 раз, если вероятность его появления в каждом испытании равна 0,36. 6. Вероятность появления события А в каждом из 225 независимых испытаний равна 0,2. Найти вероятность того, что в этих испытаниях событие А появится от 45 до 60 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=2X+4Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Составить ряд распределения случайной величины Х -числа бракованных деталей в выборке объема п =4. Вероятность того, что деталь окажется бракованной, равна 0,3. Определить вероятность того, что в выборке будет бракованных: а) ровно две детали; б) более двух деталей; в) не более двух деталей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) вероятность попадания случайной величины X в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 200мм среднее квадратическое отклонение равно 0,25мм. Стандартными считаются детали, размер которых заключен между 199,5мм и 200,5мм. Из-за нарушения технологии точность изготовления деталей уменьшилась и характеризуется средним квадратическим отклонением 0,4мм. На сколько повысился процент бракованных деталей? Вариант №9 1. Вероятность выхода из строя станка в течение одного рабочего дня равна 0,1. Какова вероятность того, что за три рабочих дня станок: а) ни разу не выйдет из строя, б) выйдет только один раз, в) выйдет хотя бы один раз. 2. В круг радиуса 8 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 5. 3. В урне 12 шаров, из них 8 – окрашенные. Найти вероятность того, что ровно 2 из 4-х вынутых наудачу шаров окрашены. 4. Три оператора радиолокационной установки производят соответственно 25; 30 и 40% всех измерений, допуская 5; 4 и 3% ошибок. А) Найти вероятность того, что проведенное измерение окажется ошибочным. В) Измерение оказалось ошибочным. Найти вероятность того, что оно было произведено первым оператором. 5. Вероятность того, что семя злака прорастет, равна 0,81. Найти вероятность того, что из 250 семян прорастет ровно 200 семян. 6. Вероятность появления события А в каждом из 300 независимых испытаний равна 0,25. Найти вероятность того, что в этих испытаниях событие А появится от 75 до 90 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-2Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Составить ряд распределения случайной величины Х -числа бракованных деталей в выборке объема п =3. Вероятность того, что деталь окажется бракованной, равна 0,9. Определить вероятность того, что в выборке будет бракованных: а) ровно три детали; б) более трех деталей; в) не более трех деталей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины X в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Масса яблока, средняя величина которой равна 150г, является нормально распределенной случайной величиной со средним квадратическим отклонением 20г. Найти вероятность того, что масса наугад взятого яблока будет заключена в пределах от 130г до 180г.
|

 ; б) плотность распределения вероятностей случайной величины X; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х:
; б) плотность распределения вероятностей случайной величины X; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х: