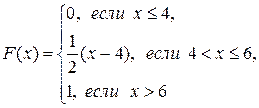3 страница. 1. Устройство состоит из трёх независимо работающих основных элементовВариант №19 1. Устройство состоит из трёх независимо работающих основных элементов. Устройство отказывает, если откажет хотя бы 1 элемент. Вероятность отказа каждого элемента за время t равна 0,1. Найти вероятность безотказной работы устройства за время t, если: а) работают только основные элементы; б) включен 1 резервный элемент; в) включены 2 резервных элемента. Предполагается, что резервные элементы работают в том же режиме, что и основные, вероятность отказа каждого резервного элемента равна 0,1 и устройство отказывает, если работает менее трёх элементов. 2. В круг радиуса 8 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 5. 3. В урне 12 шаров, из них 8 – окрашенные. Найти вероятность того, что ровно 2 из 4-х вынутых наудачу шаров окрашены. 4. В ящике содержится 12 деталей, изготовленных на заводе №1, 20 деталей – на заводе №2 и 18 деталей – на заводе №3. Вероятность того, что деталь, изготовленная на заводе №1, отличного качества равна 0,9; для деталей, изготовленных на заводах №2 и №3, эти вероятности соответственно равны 0,6 и 0,9. А) Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества. В) Извлеченная деталь оказалась отличного качества. Найти вероятность того, что она изготовлена на заводе №3. 5. Рабочий за смену проверяет на наличие брака 225 деталей. Вероятность того, что деталь не будет бракована, равна 0,8. Какова вероятность того, что не бракованных деталей будет ровно 165 штук? 6. Вероятность появления события в каждом из 600 независимых испытаний равна 0,4.Найти вероятность того, что интересующее событие появится от 210 до 252 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=2X-4Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Составить ряд распределения случайной величины Х -числа выпадений “решки” при п =6 бросаниях монеты. Определить вероятность того, что при подбрасываниях “решка” выпадет: а) ровно три раза; б) более трех раз; в) не более трех раз. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Диаметр детали, изготавливаемой на станке, - случайная величина, распределенная по нормальному закону с математическим ожиданием 25см и средним квадратическим отклонением 0,4см. Найти вероятность того, что две наудачу взятые детали имеют отклонение от математического ожидания по абсолютной величине не более 0,16см. Вариант №20 1. В мешочке содержится 10 одинаковых кубиков с номерами от 1 до 10. Наудачу извлекают по одному 3 кубика. Найти вероятность того, что последовательно появятся кубики с номерами 1, 2, 3, если кубики извлекаются: а) без возвращения; б) с возвращением (извлеченный кубик возвращается в мешочек). 2. В круг радиуса 6 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 4. 3. В урне 12 шаров, из них 6 – окрашенные. Найти вероятность того, что ровно 2 из 3-х вынутых наудачу шаров окрашены. 4. В первой урне содержится 10 шаров, из них 8 белых, во второй – 20, из них 4 белых. Из каждой урны на удачу извлекли по одному шару, а затем из этих двух шаров наудачу взят 1 шар. А) Найти вероятность того, что взят белый шар. В) Извлечен белый шар. Какова вероятность, что он был вынут из второй урны? 5. Рабочий за смену проверяет на наличие брака 150 деталей. Вероятность того, что деталь не будет бракована, равна 0,6. Какова вероятность того, что не бракованных деталей будет ровно 75 штук? 6. Вероятность появления события в каждом из 300 независимых испытаний равна 0,75.Найти вероятность того, что интересующее событие появится от 210 до 225 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=2X-3Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Всхожесть семян свеклы составляет 90%. Составить ряд распределения случайной величины Х -числа взошедших семян, если посеяно 5 семеян. Определить вероятность того, что среди пяти посеянных семян взойдет: а) ровно два; б) более двух; в) не более двух. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Пусть Х – случайная величина, подчиненная нормальному закону с математическим ожиданием 1,6 и средним квадратическим отклонением 1. Какова вероятность того, что при четырех испытаниях эта случайная величина попадет хотя бы один раз в интервал (1; 2)? Вариант №21 1. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий: а) только одно стандартно; б) оба стандартны; в) стандартно хотя бы одно. 2.. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 5. 3. В урне 10 шаров, из них 6 – окрашенные. Найти вероятность того, что ровно 2 из 3-х вынутых наудачу шаров окрашены. 4. В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. А) Найти вероятность того, что стрелок поразит мишень. В) Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него? 5. Рабочий за смену проверяет на наличие брака 400 деталей. Вероятность того, что деталь не будет бракована, равна 0,9. Какова вероятность того, что не бракованных деталей будет ровно 372 штуки? 6. Вероятность появления события в каждом из 625 независимых испытаний равна 0,36.Найти вероятность того, что интересующее событие появится от 225 до 255 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=4X-Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Стрелок произвел 6 выстрелов с вероятностью поражения цели при отдельном выстреле 0,7. Составить ряд распределения случайной величины Х -числа поражений цели. Определить вероятность того, что среди 6 выстрелов поражений мишени будет: а) ровно четыре; б) более четырех; в) не более четырех. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал (-1; 2); в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:
Построить графики функции и плотности распределения случайной величины Х. 10. Диаметр выпускаемой детали – случайная величина, подчиненная нормальному закону с математическим ожиданием 5см и средним квадратическим отклонением 0,9см. Найти вероятность того, что наудачу взятая деталь имеет диаметр в пределах от 4 до 7см. Вариант №22 1. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных изделий: а) только два изделия высшего сорта; б) ни одного изделия высшего сорта; в) хотя бы одно изделие высшего сорта. 2. В круг радиуса 9 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 4. 3. В лотерее 10 билетов, из которых 4 выигрышных. Какова вероятность, что выиграют два билета при покупке четырех билетов. 4.Число грузовых машин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина. 5. Рабочий за смену проверяет на наличие брака 600 деталей. Вероятность того, что деталь не будет бракована, равна 0,6. Какова вероятность того, что не бракованных деталей будет ровно 375 штук? 6. Вероятность появления события в каждом из 400 независимых испытаний равна 0,5.Найти вероятность того, что интересующее событие появится от 190 до 215 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=5X-Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Вероятность рождения мальчика 0,52. Составить ряд распределения случайной величины Х -числа рождений мальчиков среди 4 новорожденных. Определить вероятность того, что среди 4 новорожденных мальчиков будет: а) ровно три; б) более трех; в) не более трех. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал (3;6); в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:
Построить графики функции и плотности распределения случайной величины Х. 10. Автомат штампует детали. Контролируется длина детали Х, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактически длина изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что длина на удачу взятой детали больше 55 мм. Вариант №23 1. Устройство состоит из трёх элементов, работающих независимо. Вероятности безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0,6; 0,7 и 0,8. Найти вероятность того, что за время t безотказно будет работать: а) только один элемент; б) только два элемента; в) хотя бы один. 2. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 4. 3. В ящике 15 деталей, из них 6 – бракованные. Найти вероятность того, что ровно одна из трех вынутых деталей – бракованная. 4. Две перфораторщицы набили на разных перфокартах по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05; для второй эта вероятность равна 0,1. А) Найти вероятность того, что при сверке перфокарт будет обнаружена ошибка. В) При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица. (Предполагается, что оба перфоратора исправны.) 5. Рабочий за смену проверяет на наличие брака 192 детали. Вероятность того, что деталь не будет бракована, равна 0,75. Какова вероятность того, что не бракованных деталей будет ровно 150 штук? 6. Вероятность появления события в каждом из 225 независимых испытаний равна 0,2.Найти вероятность того, что интересующее событие появится от 45 до 60 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=5X-Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Вероятность изготовления детали высшего сорта на данном станке равна 0,6. Составить ряд распределения случайной величины Х -числа деталей высшего сорта в выборке объема п =3. Определить вероятность того, что в выборке будет высшего сорта: а) ровно две детали; б) более двух деталей; в) не более двух деталей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Диаметр выпускаемой детали – случайная величина, подчиненная нормальному закону с математическим ожиданием 5см и средним квадратическим отклонением 0,9см. Найти вероятность того, что размер диаметра наудачу взятой детали отличается от математического ожидания не более чем на 2см. Вариант №24 1. Устройство состоит из трёх элементов, работающих независимо. Вероятности безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0,6; 0,7 и 0,8. Найти вероятность того, что за время t, безотказно будут работать: а) все три элемента; б) только два элемента; в) хотя бы один элемент. 2. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 6. 3. Студент знает 25 из 30 вопросов экзамена. Найти вероятность того, что студент сдаст экзамен, если для этого достаточно ответить на 3 из 5 предложенных экзаменатором вопроса. 4. В специализированную больницу поступают в среднем 50% больных с заболеванием К, 30% – с заболеванием L, 20% – заболеванием М. Вероятности полного излечения болезни К равна 0,7, для L и M - 0,8 и 0,9 соответственно. Для обследования после лечения выбирается один пациент. А) Найти вероятность того, что пациент излечен. В) Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием K. 5. Рабочий за смену проверяет на наличие брака 100 деталей. Вероятность того, что деталь не будет бракована, равна 0,9. Какова вероятность того, что не бракованных деталей будет ровно 96 штук? 6. Вероятность появления события в каждом из 300 независимых испытаний равна 0,25.Найти вероятность того, что интересующее событие появится от 75 до 90 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=4X-2Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Игральная кость подбрасывается ровно пять раз. Составить ряд распределения случайной величины Х -числа выпадений пяти очков. Определить вероятность того, что пять очков выпадет: а) ровно два раза; б) более двух раз; в) не более двух раз. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Диаметр выпускаемой детали – случайная величина, подчиненная нормальному закону с математическим ожиданием 5см и средним квадратическим отклонением 0,9см. Установить, в каких пределах следует ожидать размер диаметра детали, чтобы вероятность не выйти за эти границы была равна 0,95.
Вариант №25 1. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлечённых двух деталей есть а) хотя бы одна стандартная; б) только одна стандартная. 2. В круг радиуса 8 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 6. 3. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают три изделия для контроля. Найти вероятность события что в полученной выборке одно изделие бракованное. 4. В группе спортсменов 20 лыжников, 6 велосипедистов, 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника-0,9; для велосипедиста-0,8; для бегуна-0,75. Выбирается наудачу один спортсмен. А) Найти вероятность того, что спортсмен выполнит норму. В) Спортсмен выполнил норму. Какова вероятность того, был выбран велосипедист? 5. Рабочий за смену проверяет на наличие брака 625 деталей. Вероятность того, что деталь не будет бракована, равна 0,8. Какова вероятность того, что не бракованных деталей будет ровно 510 штук? 6. Вероятность появления события в каждом из 625 независимых испытаний равна 0,64.Найти вероятность того, что интересующее событие появится от 400 до 430 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Баскетболист бросает мяч в кольцо 4 раз. Вероятность попадания в кольцо при одиночном бросании 0,8. Составить ряд распределения случайной величины Х -числа попаданий мяча в кольцо. Определить вероятность того, что среди четырех бросаний мяч попадет в кольцо: а) ровно три раза; б) более трех раз; в) не более трех раз. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал (4; 5); в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:
Построить графики функции и плотности распределения случайной величины Х. 10. Автомат штампует детали. Контролируется длина детали Х, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактически длина изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что длина на удачу взятой детали менее 40 мм. Вариант №26 1. Три исследователя, независимо друг от друга, производят измерения некоторой физической величины. Вероятность того, что первый исследователь допустит ошибку при считывании показаний прибора, равна 0,1. Для второго и третьего исследователей эта вероятность соответственно равна 0,15 и 0,2. Найти вероятность того, что при однократном измерении: а) только один из исследователей допустит ошибку; б) два исследователя допустят ошибку; в) хотя бы один из исследователей допустит ошибку. 2. В круг радиуса 7 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 5. 3. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают три изделия для контроля. Найти вероятность события что в полученной выборке два изделия бракованных. 4. Сборщик получил три коробки деталей, изготовленных заводом №1, и две коробки деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартна, равна 0,8, а завода №2 - 0,9. Сборщик наудачу извлёк деталь из наудачу взятой коробки. А) Найти вероятность того, что извлечена стандартная деталь. В) Извлечена стандартная деталь. Найти вероятность того, что она изготовлена заводом №2. 5. Вероятность появления события в каждом из 400 независимых испытаний равна 0,2. Найти вероятность того, что в этих испытаниях интересующее событие наступит ровно 330 раз? 6. Рабочий за смену изготавливает 150 деталей. Вероятность того, что деталь окажется первого сорта, равна 0,4. Какова вероятность того, что деталей первого сорта будет от 78 до 96 штук? 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-2Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Вероятность выигрыша по одному билету лотереи 0,1. Приобретено 4 билета. Составить ряд распределения случайной величины Х -числа выигрышей по билету в лотереи. Определить вероятность того, что среди 4 приобретенных билетов выигрышных: а) ровно четыре билета; б) более четырех билетов; в) не более четырех билетов. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 200см, среднее квадратическое отклонение равно 0,25см. Стандартными считаются детали, размер которых заключен между 199,5см и 200,5см. Найти процент стандартных деталей. Вариант №27 1. Вероятности того, что нужная сборщику деталь находится в первом, втором, третьем и четвёртом ящике соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятность того, что деталь содержится: а) в одном ящике; б) не более чем в трёх ящиках. 2. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 5. 3. В урне 9 шаров, из них 6 – окрашенные. Найти вероятность того, что ровно 2 из 3-х вынутых наудачу шаров окрашены. 4. В первом ящике содержится 20 деталей, из них 15 стандартных, во втором-30 деталей, из них 24 стандартных, в третьем-10 деталей, из них 6 стандартных. А) Найти вероятность того, что наудачу извлечённая деталь из наудачу взятого ящика стандартна. В) Извлеченная деталь стандартна. Какова вероятность того, что она была выбрана из первого ящика? 5. Вероятность появления события в каждом из 400 независимых испытаний равна 0,1. Найти вероятность того, что в этих испытаниях интересующее событие наступит ровно 372 раза? 6. Рабочий за смену изготавливает 100 деталей. Вероятность того, что деталь окажется первого сорта, равна 0,2. Какова вероятность того, что деталей первого сорта будет от 72 до 84 штук? 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-2Y. Найти и построить функцию распределения дискретной случайной величины Х.
|
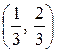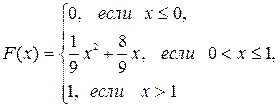
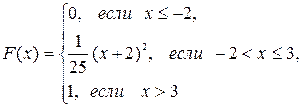
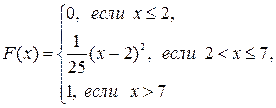
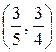; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:
; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X: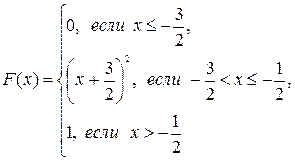
; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:
; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:
