2 страница. 1. Отдел технического контроля проверяет изделия на стандартностьВариант №10 1. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что наугад взятое изделие окажется бракованным, равна 0,15. Проверено три изделия. Какова вероятность того, что среди них бракованных: а) все три, б) только два в) хотя бы одно. 2. В круг радиуса 6 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 4. 3. В урне 12 шаров, из них 6 – окрашенные. Найти вероятность того, что ровно 2 из 3-х вынутых наудачу шаров окрашены. 4. Имеется два мешка семян одной культуры первой партии, всхожестью 90% и один мешок той же культуры второй партии, всхожестью 85%. Наугад взяли мешок и посадили одно зерно. А) Какова вероятность того, что оно взойдет? В) Зерно взошло. Какова вероятность того, что оно из первой партии? 5. Рабочий за смену изготавливает 300 деталей. Вероятность того, что деталь окажется первого сорта, равна 0,75. Какова вероятность того, что деталей первого сорта будет ровно 240 штук? 6. Вероятность появления события А в каждом из 625 независимых испытаний равна 0,64. Найти вероятность того, что в этих испытаниях событие А появится от 400 до 430 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=2X+4Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Составить ряд распределения случайной величины Х -числа бракованных деталей в выборке объема п =5. Вероятность того, что деталь окажется бракованной, равна 0,2. Определить вероятность того, что в выборке будет бракованных: а) ровно четыре детали; б) более четырех деталей; в) не более четырех деталей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины X в интервал (1; 3); в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х:
Построить графики функции и плотности распределения случайной величины Х. 10. Устройство состоит из 20 однотипных независимо работающих элементов. Вероятность безотказной работы каждого элемента за 10 часов равна 0,9. Оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом отказов за 10 часов окажется меньше двух. Вариант №11 1. В ящике в случайном порядке разложены 20 деталей, причем пять из них стандартные. Рабочий берет наудачу три детали. Найти вероятность того, что по крайней мере одна из взятых деталей окажется стандартной. 2.. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 5. 3. В урне 10 шаров, из них 6 – окрашенные. Найти вероятность того, что ровно 2 из 3-х вынутых наудачу шаров окрашены. 4. На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 3% брака, второй – 2%, а третий – 4%. А) Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 1000, со второго – 2000 и с третьего – 2500 деталей. В) Деталь оказалась бракованной. Найти вероятность того, что она изготовлена на втором автомате. 5. Вероятность попадания в цель при одном выстреле составляет 0,9. Найти вероятность 372 попаданий при 400 выстрелах. 6. Вероятность появления события А в каждом из 150 независимых испытаний равна 0,4. Найти вероятность того, что в этих испытаниях событие А появится от 79 до 99 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=2X+4Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Составить ряд распределения случайной величины Х -числа выпадений “герба” при п =5 бросаниях монеты. Определить вероятность того, что при подбрасываниях “герб” выпадет: а) ровно два раза; б) более двух раз; в) не более двух раз. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины X в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Нормально распределенная случайная величина - длина детали с математическим ожиданием 150мм и средним квадратическим отклонением 0,5мм. Какую точность размера детали можно гарантировать с вероятностью 0,95. Вариант №12 1. Три оператора радиолокационной установки производят соответственно 25; 30 и 40% всех измерений, допуская 5; 4 и 3% ошибок. Измерение оказалось ошибочным. Найти вероятность того, что оно произведено первым оператором. 2. В круг радиуса 9 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 4. 3. В лотерее 10 билетов, из которых 4 выигрышных. Какова вероятность, что выиграют два билета при покупке четырех билетов. 4. Три оператора радиолокационной установки производят соответственно 25; 30 и 40% всех измерений, допуская 5; 4 и 3% ошибок. А) Найти вероятность того, что случайно проверенное измерение окажется ошибочным. В) Измерение оказалось ошибочным. Найти вероятность того, что оно произведено вторым оператором. 5. Всхожесть семян оценивается вероятностью 0,8. Какова вероятность того, что из 625 посеянных семян взойдет ровно 510? 6. Вероятность появления события А в каждом из 250 независимых испытаний равна 0,6. Найти вероятность того, что в этих испытаниях событие А появится от 120 до 220 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Всхожесть семян ржи составляет 80%. Составить ряд распределения случайной величины Х -числа взошедших семян, если посеяно 4 семени. Определить вероятность того, что среди четырех посеянных семян взойдет: а) ровно два; б) более двух; в) не более двух. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины X в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Пусть средний вес зерна составляет 0,25г, среднее квадратическое отклонение равно 0,05г. Определить вероятность того, что вес наудачу взятого зерна окажется в пределах от 0,22г до 0,28г.
Вариант №13 1. Найдите вероятность того, что наудачу взятое двузначное число окажется кратным либо 4, либо 5, либо тому и другому одновременно. 2. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 4. 3. В урне 13 шаров, из них 6 – окрашенные. Найти вероятность того, что ровно 2 из 4-х вынутых наудачу шаров окрашены. 4. Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02; для второго – 0,03; для третьего – 0,04. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше, чем второго, а третьего в два раза меньше, чем второго. А) Найти вероятность того, что наугад извлеченная деталь имеет брак. В) Из ящика наугад взята одна деталь, которая оказалась бракованной. Какова вероятность того, что она произведена на первом станке? 5. Найти приближённо вероятность того, что при 225 испытаниях событие наступит ровно 158 раз, если вероятность его появления в каждом испытании равна 0,64. 6. Вероятность появления события А в каждом из 450 независимых испытаний равна 0,9. Найти вероятность того, что в этих испытаниях событие А появится от 250 до 295 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Стрелок произвел 6 выстрелов с вероятностью непопадания при отдельном выстреле 0,1. Составить ряд распределения случайной величины Х -числа непопаданий. Определить вероятность того, что среди 6 выстрелов непоражений мишени будет: а) ровно четыре; б) более четырех; в) не более четырех. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины X в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Масса груши, средняя величина которой равна 100г, является нормально распределенной случайной величиной со средним квадратическим отклонением 20г. Найти вероятность того, что масса наугад взятой яблока будет заключена в пределах от 90г до 180г. Вариант №14 1. В урне находятся 10 белых, 15 черных, 20 синих и 25 красных шаров. Найдите вероятность того, что вынутый шар окажется: а) белым, б) черным или красным. 2. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 6. 3. Студент знает 25 из 30 вопросов экзамена. Найти вероятность того, что студент сдаст экзамен, если для этого достаточно ответить на 3 из 5 предложенных экзаменатором вопроса. 4. Имеется два мешка семян одной культуры первой партии, всхожестью 90% и один мешок той же культуры второй партии, всхожестью 85%. Наугад взяли мешок и посадили одно зерно. А) Найти вероятность всхода случайно выбранного зерна. В) Зерно взошло. Какова вероятность того, что оно из второй партии? 5. Вероятность попадания в цель при одном выстреле составляет 0,6. Найти вероятность 375 попаданий при 600 выстрелах. 6. Вероятность появления события А в каждом из 600независимых испытаний равна 0,8. Найти вероятность того, что в этих испытаниях событие А появится от 510 до 525 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=2X+4Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Вероятность рождения мальчика 0,51. Составить ряд распределения случайной величины Х -числа рождений мальчиков среди 5 новорожденных. Определить вероятность того, что среди 5 новорожденных мальчиков будет: а) ровно три; б) более трех; в) не более трех. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины X в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Процент всхожести семян равен 95%. Оценить вероятность того, что из 1000 посеянных семян взойдет от 870 до 950 семян включительно. Вариант №15 1. В ящике в случайном порядке расположены 10 деталей, из которых 4 стандартных. Контролер взял наудачу 3 детали. Найдите вероятность того, что хотя бы одна из взятых деталей оказалась стандартной, только две стандартных, ни одной стандартной. 2. В круг радиуса 8 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 6. 3. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают три изделия для контроля. Найти вероятность события что в полученной выборке одно изделие бракованное. 4. На фабрике на машинах А, В С производят соответственно 35; 25 и 40% всех изделий. В их продукции брак составляет соответственно 15; 10 и 5%. А) Найти вероятность того, случайно выбранное изделие окажется бракованным? В) Выбранное изделие оказалось дефектным. Найти вероятность того, что оно было изготовлено на машине В. 5. Рабочий за смену изготавливает 625 деталей. Вероятность того, что деталь окажется первого сорта, равна 0,64. Какова вероятность того, что деталей первого сорта будет ровно 370 штук? 6. Вероятность появления события А в каждом из 550 независимых испытаний равна 0,65. Найти вероятность того, что в этих испытаниях событие А появится от 425 до 450 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Вероятность изготовления детали высшего сорта на данном станке равна 0,4. Составить ряд распределения случайной величины Х -числа деталей высшего сорта в выборке объема п =4. Определить вероятность того, что в выборке будет высшего сорта: а) ровно две детали; б) более двух деталей; в) не более двух деталей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Случайные отклонения размера детали от номинала распределены нормально. Математическое ожидание размера детали равно 210мм, среднее квадратическое отклонение равно 0,25мм. Стандартными считаются детали, размер которых заключен между 209,5мм и 210,5мм. Найти процент стандартных деталей. Вариант №16 1. Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что среди 2 наудачу выбранных билетов: а) оба окажутся выигрышными; б) хотя бы один выигрышный; в) только один выигрышный. 2. В круг радиуса 7 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 5. 3. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают три изделия для контроля. Найти вероятность события что в полученной выборке два изделия бракованных. 4. Имеются три одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором-1о белых и 10 черных шаров, в третьем-20 черных шаров. А) Какова вероятность того, случайно выбранный шар окажется белым? В) Извлечен белый шар. Найти вероятность того, что шар вынут из первого ящика. 5. Рабочий за смену проверяет на наличие брака 400 деталей. Вероятность того, что деталь не будет бракована, равна 0,8. Какова вероятность того, что не бракованных деталей будет ровно 330 штук? 6. Вероятность появления события в каждом из 150 независимых испытаний равна 0,6.Найти вероятность того, что интересующее событие появится от 78 до 96 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=X-4Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Игральная кость подбрасывается ровно три раза. Составить ряд распределения случайной величины Х -числа выпадений “тройки”. Определить вероятность того, что “тройка” выпадет: а) ровно два раза; б) более двух раз; в) не более двух раз. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Считается, что отклонение длины изготавливаемой детали от стандарта является случайной величиной, распределенной по нормальному закону. Если стандартная длина равна 40см и среднее квадратическое отклонение равно 0,4см, то какую точность длины изделия можно гарантировать с вероятностью 0,8? Вариант №17 1. Для сигнализации об аварии установлены 2 независимо работающих сигнализатора. Вероятность того, что при аварии сработает сигнализатор, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает: а) только один сигнализатор; б) оба сигнализатора; в) хотя бы один сигнализатор. 2. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 5. 3. В урне 9 шаров, из них 6 – окрашенные. Найти вероятность того, что ровно 2 из 3-х вынутых наудачу шаров окрашены. 4. В вычислительной лаборатории имеются 6 клавишных автоматов и 4 полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна 0,95; для полуавтомата эта вероятность равна 0,8. Студент производит расчет на наудачу выбранной машине. А) Найти вероятность того, что до окончания расчета машина не выйдет из строя. В) Машина не вышла из строя. Какова вероятность того, что студент производил расчет на полуавтомате? 5. Рабочий за смену проверяет на наличие брака 300 деталей. Вероятность того, что деталь не будет бракована, равна 0,75. Какова вероятность того, что не бракованных деталей будет ровно 240 штук? 6. Вероятность появления события в каждом из 100 независимых испытаний равна 0,8.Найти вероятность того, что интересующее событие появится от 72 до 84 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X-Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Баскетболист бросает мяч в кольцо 5 раз. Вероятность попадания в кольцо при одиночном бросании 0,7. Составить ряд распределения случайной величины Х -числа попаданий мяча в кольцо. Определить вероятность того, что среди пяти бросаний мяч попадет в кольцо: а) ровно три раза; б) более трех раз; в) не более трех раз. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Масса вагона – случайная величина, распределенная по нормальному закону с математическим ожиданием 65т и средним квадратическим отклонением 0,9т. Найти вероятность того, что очередной вагон имеет массу не более 70т, но не менее 60т. Вариант №18 1. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадет: а) только один из стрелков; б) хотя бы один из стрелков; в) только второй стрелок. 2. В круг радиуса 10 случайным образом брошена точка так, что ее любое расположение в круге равновозможно. Найти вероятность того, что она окажется внутри лежащего в круге квадрата со стороной 6. 3. В урне 10 шаров, из них 7 – окрашенные. Найти вероятность того, что ровно 2 из 3-х вынутых наудачу шаров окрашены. 4. В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела- 0,7. А) Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки. В) Стрелок поразил мишень одним выстрелом. Какова вероятность того, что выстрел был произведен из винтовки без оптического прицела? 5. Рабочий за смену проверяет на наличие брака 625 деталей. Вероятность того, что деталь не будет бракована, равна 0,64. Какова вероятность того, что не бракованных деталей будет ровно 370 штук? 6. Вероятность появления события в каждом из 400 независимых испытаний равна 0,9.Найти вероятность того, что интересующее событие появится от 345 до 372 раз. 7. Независимые дискретные величины X и Y заданы законами распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3X+Y. Найти и построить функцию распределения дискретной случайной величины Х. 8. Вероятность выигрыша по одному билету лотереи 0,3. Приобретено 6 билетов. Составить ряд распределения случайной величины Х -числа выигрышей по билету в лотереи. Определить вероятность того, что среди 6 приобретенных билетов выигрышных: а) ровно четыре билета; б) более четырех билетов; в) не более четырех билетов. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. 9. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X, б) вероятность попадания случайной величины в интервал
Построить графики функции и плотности распределения случайной величины Х. 10. Мастерская изготавливает стержни, длина которых l представляет собой случайную величину, распределенную по нормальному закону с математическим ожиданием и средним квадратическим отклонением, равными соответственно 25 и 0,1см. Найти вероятность того, что отклонение длины стержня в ту или другую сторону от математического ожидания не превзойдет 0,25см.
|
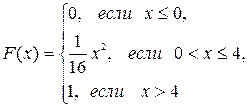
; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х: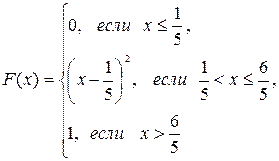
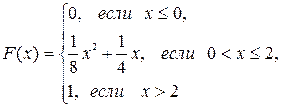
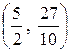; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х: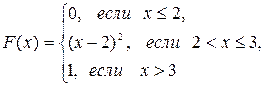
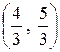; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х: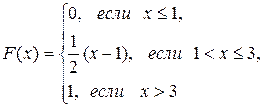
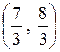; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X: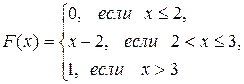
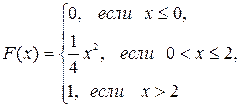
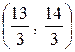; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:
