Метод головних компонент
Цей метод призначений для оцінювання моделей великого розміру, а також для оцінки параметрів моделі, якщо до неї входять мультиколінеарні змінні. Існують різні модифікації методу головних компонентів, які різняться між собою залежно від того, що береться за основу при визначенні ортогональних змінних — коваріаційна чи кореляційна матриця незалежних змінних. Нехай маємо матрицю Х, яка описує незалежні змінні моделі. Оскільки спостереження, що утворюють матрицю Х, як правило, корельовані між собою, то можна поставити питання про кількість реально незалежних змінних, які входять до цієї матриці. Точніше, ідея методу полягає в тому, щоб перетворити множину змінних Х на нову множину попарно некорельованих змінних, серед яких перша відповідає максимально можливій дисперсії, а друга — максимально можливій дисперсії в підпросторі, який є ортогональним до першого, і т.д. Нехай нова змінна запишеться:
У матричній формі
де Суму квадратів елементів вектора подамо у вигляді:
Звідси необхідно вибрати такий вектор
Оскільки Z 1 = Xa 1, то максимізація a 1 буде максимізувати Z 1, а Z 1 характеризує вклад змінної Z 1 в загальну дисперсію. Задача тепер полягає в тому, щоб максимізувати
де Узявши
Звідси бачимо, що Підставивши значення (6.18) у (6.16), дістанемо:
Отже, потрібно для значення Визначимо тепер 1) 2) Друга умова забезпечить відсутність кореляції між Для розв’язування цієї задачі функцію Лагранжa запишемо у вигляді
де Узявши Цей процес триває доти, доки всі m характеристичних значень матриці
Отже, головні компoненти матриці X задаються матрицею
розміром n ´ m.
Вираз (3.22) означає, що головні компоненти дійсно попарно некорельовані, а їх дисперсії визначаються так:
Співвідношення Зауважимо, що вектори вихідних даних (матриця X) повинні мати однакові одиниці вимірювання, бо в противному разі дуже важко дати змістовне тлумачення поняттю загальної варіації змінних X і розкладанню цієї варіації на складові, виконаному відповідно до внеску кожного з векторів, якими подаються головні компоненти. Іноді буває важко надати конкретного змісту знайденим головним компонентам. Для цього можна обчислити коефіцієнти кореляції кожного компонента з різними змінними X. Так, наприклад, візьмемо перший головний компонент Z 1 і знайдемо коефіцієнти його кореляції її з усіма змінними X. Для цього потрібно обчислити перехресні добутки між головним компонентом Z 1 і кожною з пояснювальних змінних X. Оскільки
маємо коефіцієнти кореляції для першого компонента:
У загальному випадку коефіцієнт кореляції між
Частка різних головних компонентів в варіації Визначивши всі головні компоненти і відкинувши ті з них, які відповідають невеликим значенням характеристичних коренів, знаходимо зв’язок залежної змінної Y з основними головними компонентами, а далі з допомогою оберненого перетворення повертаємося від параметрів моделі з головними компонентами до знаходження оцінок параметрів змінних X. Алгoритм головних компонентів Крок 1. Нормалізація всіх пояснювальних змінних:
Крок 2. Обчислення кореляційної матриці
Крок 3. Знаходження характеристичних чисел матриці r з рівняння
де E — одинична матриця розміром m ´ m. Крок 4. Власні значення Крок 5. Обчислення власних векторів
за таких умов:
Крок 6. Знаходження головних компонентів — векторів
Головні компоненти мають задовольняти умови:
Крок 7. Визначення параметрів моделі
Крок 8. Знаходження параметрів моделі
|

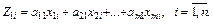
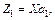 (3.15)
(3.15)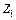 — вектор значень нової змінної;
— вектор значень нової змінної; 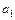 — m -вимірний власний вектор матриці
— m -вимірний власний вектор матриці 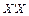 .
. (3.16)
(3.16)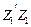 , але на вектор
, але на вектор 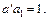 (3.17)
(3.17)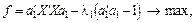
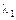 — множник Лагранжа.
— множник Лагранжа.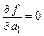 , дістанемо
, дістанемо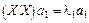 . (3.19)
. (3.19)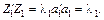 (3.20)
(3.20)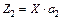 . При цьому вектор
. При цьому вектор 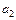 має максимізувати вираз
має максимізувати вираз 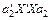 за таких умов:
за таких умов: ;
;
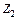 і
і 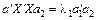 , причому вона дорівнює нулю лише тоді, коли
, причому вона дорівнює нулю лише тоді, коли 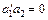 .
.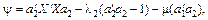
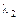 і
і 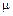 — множники Лагранжa.
— множники Лагранжa. і
і  , дістанемо
, дістанемо 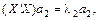 де для значення
де для значення 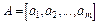 .
.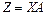 (3.21)
(3.21)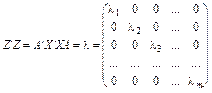 . (3.22)
. (3.22)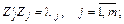 (3.23)
(3.23)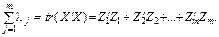
 характеризують пропорційний внесок кожного з векторів у загальну варіацію змінних X, причому оскільки ці компоненти ортогональні, сума всіх внесків дорівнює одиниці.
характеризують пропорційний внесок кожного з векторів у загальну варіацію змінних X, причому оскільки ці компоненти ортогональні, сума всіх внесків дорівнює одиниці.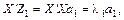
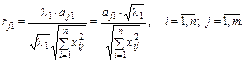 (3.24)
(3.24)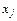 і
і 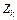
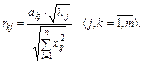 (3.25)
(3.25)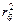 , а оскільки компоненти не корелюють один з одним, то сума їх часток дорівнює одиниці.
, а оскільки компоненти не корелюють один з одним, то сума їх часток дорівнює одиниці.

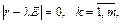
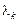 упорядковуються за абсолютним рівнем вкладу кожного головного компонента до загальної дисперсії.
упорядковуються за абсолютним рівнем вкладу кожного головного компонента до загальної дисперсії.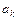 розв’язуванням системи рівнянь
розв’язуванням системи рівнянь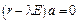

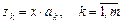
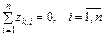 ;
; ;
;
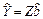 :
: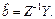
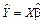 :
:



