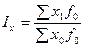Пример. В текущем, отчётном году предприятие произвело 120 тыс.т
В текущем, отчётном году предприятие произвело 120 тыс.т. продукции вместо 100 тыс.т. в прошлом базисном, году. Цены за каждую тонну этой продукции снизились с 20 до 18 рублей; а её общая стоимость возросла с 2 000 до 2 160 тыс. руб. В данном примере можно вычислить три индекса: индекс объёма продукции: Полученные индексы показывают, что объём продукции и её стоимость возросла в отчётном году по сравнению с базисным в 1,2 и 1,08 раза, а цены, наоборот, снизились до 1,9 их базисного уровня. Все три индекса образуют систему показателей — сомножителей: Приведем формулы расчета индивидуальных индексов наиболее часто используемых экономических показателей.
Приведенные индексы взаимосвязаны, например:
Общие (сводные) индексы выражают обобщающие результаты совместного изменения всех единиц, образующих статистическую совокупность. Пример, показатель изменения объема реализации товарной массы продуктов питания по отдельным периодам будет общим индексом физического объема товарооборота. В зависимости от цели исследования и наличия исходных данных, общие индексы могут быть представлены в трех формах: агрегатной, средней арифметической, средней гармонической. Исходной формой выражения общих индексов является агрегатная форма; средние индексы получаются в результате ее преобразования. Основными элементами агрегатного индекса выступают индексируемая величина и вес индекса. Индексируемая величина – признак, изменение которого характеризует индекс. Вес индекса (соизмеритель) – величина тесно связанная с индексируемой величиной и служащая для целей соизмерения индексируемых величин. Вес индекса необходим для перехода от натуральных измерителей разнородных единиц При этом произведение Общая формула агрегатного индекса может быть записана следующим образом:
где Таким образом, в числителе и знаменателе агрегатной формы индекса находятся просуммированные произведения двух величин, одна из которых — индексируемая величина (в числителе содержится значение, относящееся к отчетному периоду, а в знаменателе — к базисному), а другая — постоянная, являющаяся весом индекса. При этом суммируемых произведений столько, сколько единиц исследуемой совокупности входит в изучаемое явление. Общие индексы строят для количественных и качественных показателей. При этом веса индекса · индексы качественных показателей строятся с весами отчетного периода. Тогда формула агрегатного индекса примет вид
· индексы количественных показателей строятся с весами базисного периода. Формула агрегатного индекса в этом случае имеет следующий вид:
Такое построение агрегатных индексов позволяет получить систему взаимосвязанных индексов и провести анализ влияния отдельных факторов на изменение обобщающих результативных показателей. К количественным относят показатели, характеризующие физические размеры явления, например, производство продукции в натуральном выражении, количество проданного товара, численность работающих, объем промышленно-производственных фондов и т.д. (как правило, в названии количественного показателя содержатся слова «объем», «число», «численность», «количество»; при этом используются простые единицы измерения — метры, килограммы, тонны, штуки, рубли). Качественный показатель используется для экономической (качественной) характеристики количественной единицы совокупности. Это цена за единицу товара (продукции), себестоимость единицы продукции, фондоотдача, фондоемкость, средняя заработная плата (единица измерения качественного показателя сложная — руб./шт., руб./руб., руб./чел. и т.д.). Важной особенностью агрегатных индексов является то, что они обладают синтетическими и аналитическими свойствами; другими словами в теории индексов существуют два направления возможной анализа сводных индексов: синтетическое и аналитическое. Различие между ними состоит в интерпретации полученных результатов. Синтетические свойства индексов состоят в том, что посредством индексного метода производится соединение (агрегирование) в целом разнородных единиц статистической совокупности. При синтетическом подходе индекс рассматривается как показатель, характеризующий среднее изменение уровня индексируемой величины. Аналитические свойства индексов состоят в том, что посредством индексного метода определяется влияние факторов на изменение изучаемого показателя. Аналитический подход подразумевает использование индекса как меры изменения уровня результативного показателя (получаемого в виде произведения индексируемой величины и ее веса) под влиянием изменений индексируемой величины
|

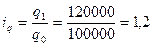 или 120%; индекс цен:
или 120%; индекс цен: 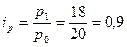 или 90%; индекс стоимости продукции:
или 90%; индекс стоимости продукции: 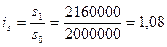 или 108%.
или 108%.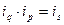 или
или 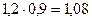 .
.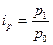
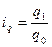
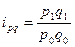
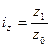
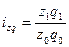
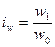
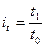

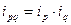 ;
; 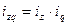 ;
; 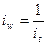
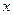 статистической совокупности к однородным показателям. В индексные отношения вводятся специальные сомножители
статистической совокупности к однородным показателям. В индексные отношения вводятся специальные сомножители 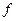 индексируемых величин, через что достигается сопоставимость разнородных единиц в сложных статистических совокупностях. Эти сомножители и есть веса индекса или соизмерители. В качестве весов
индексируемых величин, через что достигается сопоставимость разнородных единиц в сложных статистических совокупностях. Эти сомножители и есть веса индекса или соизмерители. В качестве весов 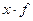 имеет экономическое содержание и может суммироваться по всем единицам разнородной совокупности [например, умножив количества товаров на их цены, получим объемы продаж в денежном выражении (товарооборот), которые можно суммировать по разным видам товаров].
имеет экономическое содержание и может суммироваться по всем единицам разнородной совокупности [например, умножив количества товаров на их цены, получим объемы продаж в денежном выражении (товарооборот), которые можно суммировать по разным видам товаров]. ,
,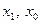 – значения индексируемой величины, соответственно, в отчетном и базисном периоде;
– значения индексируемой величины, соответственно, в отчетном и базисном периоде; 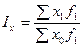 ;
;