Условия применения факторного анализа. Практическое выполнение факторного анализа начинается с проверки его условий
Практическое выполнение факторного анализа начинается с проверки его условий. В обязательные условия факторного анализа входят: · Все признаки должны быть количественными. · Число наблюдений должно быть в два раза больше числа переменных. · Выборка должна быть однородна. · Исходные переменные должны быть распределены симметрично. Факторный анализ осуществляется по коррелирующим переменным Главными целями факторного анализа являются сокращение числа переменных (редукция данных) и определение структуры взаимосвязей между переменными, т.е. классификация переменных. Поэтому факторный анализ используется или как метод сокращения данных, или как метод классификации переменных. Сокращение достигается путем выделения скрытых общих факторов, объясняющих связи между наблюдаемыми признаками (переменными) объекта, т.е. вместо исходного набора переменных появится возможность анализировать данные по выделенным факторам, число которых значительно меньше исходного числа взаимосвязанных переменных. Взаимосвязи между переменными можно обнаружить с помощью диаграммы рассеяния. Полученная путем подгонки линия регрессии дает графическое представление зависимости. Если определить новую переменную на основе линии регрессии, изображенной на этой диаграмме, то такая переменная будет включать наиболее существенные черты обеих переменных. Итак, произошло сокращение числа переменных — две заменили одной. Причем новый фактор (переменная) является линейной комбинацией двух исходных. Приведенный пример, в котором две коррелированные переменные объединены в один фактор, показывает главную идею факторного анализа. В основном процедура выделения факторов подобна вращению, максимизирующему дисперсию исходного пространства переменных. Например, на диаграмме рассеяния можно рассматривать линию регрессии как ось X, повернув ее так, что она совпадает с прямой регрессии. Этот тип вращения называется вращением, максимизирующим дисперсию (варимакс), так как цель вращения заключается в максимизации изменчивости новой переменной (фактора) и минимизации разброса исходных переменных. Если пример с двумя переменными распространить на большее число переменных, то вычисления становятся сложнее, однако основной принцип представления двух или более зависимых переменных одним фактором остается в силе. Число наблюдаемых объектов может быть большим и взаимосвязи между ними чрезвычайно сложными. Однако наблюдая объект, выдвигаем гипотезу, что существует небольшое число факторов, которые влияют на измеряемые параметры. Естественно желание выделить как можно меньшее число скрытых общих факторов и чтобы выделенные факторы как можно точнее приближали наблюдаемые параметры, описывали связи между ними. Выделяемые таким образом факторы называют общими, так как они воздействуют на все признаки (параметры) объекта, а не на какой-то один признак или группу признаков. Эти факторы являются гипотетическими, скрытыми, их нельзя измерить непосредственно, однако существуют статистические методы их выделения. Рассмотрим модель факторного анализа. Пусть задана система переменных Х1, Х2,..,Хп. Например, X, — производительность труда, Х3 — фондоотдача Хп — себестоимость. Значения переменных или признаков Хр Х2,Хп известны для каждого из N предприятий (объектов). Представим исходную информацию в виде матрицы.X = хji размерности (n х N). Каждая строка состоит из значений одного показателя для каждого из N объектов исследования. Предполагается, что каждый элемент этой матрицы хji является результатом воздействия некоторого числа m гипотетических общих факторов и одного характерного фактора
где ajr — весовой коэффициент j-й переменной на r-м общем факторе или нагрузка j-й переменной на r-м общем факторе; fri — значение r-го общего фактора на i-м объекте исследования; d, — нагрузка или весовой коэффициент j-й переменной на j-м характерном факторе; Uji— значение j-го характерного фактора на i-м объекте исследования; j= 1,…,п; i = 1,..., N;r= 1,... т; т << п. Так как массив данных X = представляет величины различной размерности, то для того чтобы перейти к безразмерным величинам, пронормируем элементы массива.
где Xj — выборочное среднеей переменной (признака); S, — выборочная дисперсия j-й переменной. После этих преобразований получим
где ajm — неизвестные коэффициенты, называемые факторными нагрузками; v. называется остатком (невязкой), или остаточным специфическим фактором. Задача состоит в том, чтобы оценить а)т некоторым оптимальным образом. Обычно в моделях факторного анализа предполагаются выполненными следующие предположения: • Хji имеют многомерное нормальное распределение; • общие факторы f 1i являются либо некоррелированными случайными величинами с дисперсией 1, либо неизвестными случайными параметрами; • остатки (остаточные факторы) U1i имеют нормальное распределение, не коррелированны между собой и не зависят от общих факторов. Если в качестве критерия оптимальности используют минимум расхождения между ковариационной матрицей исходных признаков и той, которая получается после оценивания факторных нагрузок (мера «расхождения» двух матриц, в данном случае есть просто евклидова норма их разности), то приходят к методу главных компонент. Если критерием оптимальности является максимальная близость исходных корреляций признаков к тем, которые получены в модели после оценивания нагрузок, то говорят о методах анализа главных факторов. Правая часть выражения (3) линейна и напоминает выражение для регрессионного анализа. Однако здесь есть большая разница. В регрессионном анализе система переменных предполагается измеряемой непосредственно (например, взяты из отчетной документации предприятий). Однако в факторном анализе общие и характерные факторы являются гипотетическими (неизвестными). Их нужно оценить методами математической статистики и линейной алгебры.
|

 (1)
(1) (2)
(2)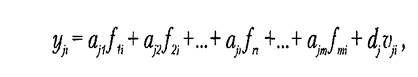 (3)
(3)


