Описание модуля Factor Analysis

В меню Statistics щелкните по Multivariate Exploratory Techniques (много­мерные исследовательские методы) и выберите команду Factor Analysis (анализ факторов). Откроется стартовая панель модуля. Рассмотрим все его компоненты и опишем некоторые из них. В ноле Input File (файл входных данных) надо ука­зать тин исходного файла, с которым предстоит работать. В модуле возможны следующие типы исходных данных:

• Correlation Matrix (корреляционная матрица);

• Raw Data (исходные данные).

Выберите, например, Raw Data. Это обычный файл данных, где по строкам за­писаны значения переменных. В правом нижнем углу окна, за всеми функциональ­ными кнопками находится поле MD deletion (обработка пропущенных значений). В этом поле необходимо задать один из способов, которым будут обрабатываться при анализе пропущенные значения (незаполненные ячейки);

• Casewise (способ исключения пропущенных случаев);

• Pairwise (парный способ исключения пропущенных значений);

• Mean Substitution (подстановка среднего вместо пропущенных значений).

Способ Casewise состоит в том, что в электронной таблице, содержащей дан­ные, игнорируются все строки (наблюдения), в которых имеется хотя бы одно пропущенное значение. Это относится ко всем переменным. Итак, в таблице оста­ются только те наблюдения, в которых нет ни одного пропуска.

В способе Pairwise игнорируются пропущенные наблюдения не для всех пере­менных, а лишь для выбранной пары. Все наблюдения, в которых нет пропусков, используются в обработке, например, при поэлементном вычислении корреляци­онной матрицы, когда последовательно рассматриваются все пары переменных.

Способ Mean Substitution предполагает при выполнении анализа заполнение пустых клеток средними значениями.

Очевидно, в способе Pairwise остается больше наблюдений для обработки, чем в способе Casewise. Тонкость, однако, состоит в том, что в способе Paimise оценки различных коэффициентов корреляции строятся но различному числу наблюде­ний. Выберите, например, способ Casewise.

Дальнейшее рассмотрение требует работы уже с конкретными данными, по­этому следующим действием откройте файл, содержащий исходные данные для анализа (если он еще не открыт). В качестве примера рассмотрите имеющийся в программе STATISTICA файл Factor.sta из библиотеки Examples. Об этом фай­ле шла речь при изучении модуля Canonical Analysis. Теперь, когда есть данные для анализа, выбран способ обработки пропущенных значений, перейдем к выбо­ру переменных, для которых будем проводить факторный анализ.

Для того чтобы сделать это, задействуйте кнопку Variables. Появится окно выбора переменных Select the variables for the factor analysis (выбрать перемен­ные для факторного анализа). Кнопка Select All (выбрать все) позволяет выбрать все переменные сразу.

Щелкните в стартовом окне модуля кнопкой ОК. Программа начнет ана­лиз выбранных неременных, появится окно Define Method of Factor Extraction (определить метод выделения факторов). В информационной части окна сообщается, что пропущенные значения обработаны мето­дом Casewise. Обработано 100 случаев и 100 случаев принято для дальнейших вычислений. Корреляционная матрица вычислена для 10 переменных. Ниж­няя часть текущего диалогового окна состоит из трех вкладок. Выделите вкладку Descriptives, так как факторный анализ надо начинать с вычисле­ния корреляционной матрицы. Ее анализ позволит оценить степень коррели­рованное™ переменных между собой. И если эта степень окажется высокой, то данные переменные можно объединять в один фактор. А процедура вычис­ления корреляционной матрицы доступна именно из этого окна.

Кнопка Review corelations, means, standard deviations предназначена для построения корреляционной матрицы, вычисления средних, стандартных отклонений.

Кнопка Compute multiple regression analyses осуществляет запуск процедуры множественного регрессионного анализа.

 

 

 

Нажмите кнопку Review corelations, means, standard deviations. Откроется окно Review Descriptive Statistics (обзор описательных статистик), на вкладке Quick (Advanced) нажмите кнопку Correlations. На рис. 14.2 изображен фраг­мент корреляционной матрицы, из которого видно, что коэффициенты корреля­ции переменных WORK с переменными НОМЕ имеют малые значения, в то время кай с другими группами переменных принимают большие значения. Этот факт отразится на результатах последующих этапов факторного анализа.

Нажмите кнопку Cancel и вернитесь в исходное окно Define Method of Factor Extraction. Выделите вкладку Advanced, на этой вкладке имеются следующие поля:

- Maximum no. of factors (максимальное число факторов);

- Minimum eigenvalue (минимальное собственное значение).

В поле Minimum eigenvalue устанавливается минимальное собственное значе­ние, т.е. если собственные значения окажутся меньше, чем установленный здесь минимум, то они игнорируются.

 

 

В поле Maximum no. of factors пользователь устанавливает количество факто­ров, которые необходимо выделить для анализируемых данных. Можно устано­вить любое значение, не превышающее количество переменных, но не любой по­лученный таким образом результат окажется правильным. Для того чтобы получить интерпретируемый результат, на практике используют несколько по­лезных критериев.

В методе главных компонент по умолчанию предполагается, что дисперсии всех переменных равны 1, Тогда общая дисперсия равна общему числу перемен­ных (для нашего примера — 10). Это означает, что наибольшая изменчивость, ко­торая потенциально может быть выделена, равна 10. Максимально возможное число выделяемых факторов равно числу переменных. Каждому фактору соот­ветствуетдисперсия, объясненная этим фактором. Дисперсии, соответствующие факторам, называются собственными значениями.

Для просмотра собственных значений факторов в окне Define Method of Factor Extraction произведите следующие установки параметров: Maximum по, of factors = 10 и Minimum eigenvalue = 0. Далее нажмите ОК. В открывшемся окне Factor Analysis Results нажмите кнопку Eigenvalues, появится таблица с собст­венными числами (А).

Во втором столбце таблицы приведены дисперсии выделенных факторов — собственные числа. В третьем столбце для каждого фактора приводится процент от общей дисперсии (в данном примере она равна 10). Как видно, первый фактор объясняет 61% общей дисперсии, второй фактор — 18% и т.д. Четвертый столбец содержит накопленную или кумулятивную дисперсию. Как только получена ин­формация о том, сколько дисперсии выделил каждый фактор, можно перейти к вопросу, сколько факторов следует оставить.

 

 

Критерий Кайзера. Сначала можете отобрать только факторы с собственны­ми значениями, большими 1. По существу это означает, что если фактор не вы­деляет дисперсию, эквивалентную, по крайней мере, дисперсии одной перемен­ной, то он опускается. Этот критерий предложен Кайзером и является, вероятно, наиболее широко используемым. В приведенном примере на основе данного критерия выделяются только два фактора, так как остальные не подхо­дят под условие, наложенное на собственные значения.

 

(А)

 

 

Критерий каменистой сыпи. Критерий является графическим методом, впервые предложенный Кеттелем.

Надо изобразить собственные значения, представленные в таблице в виде гра­фика. Кэттель предложил найти такое место на графике, где убывание собствен­ных значений слева направо максимально замедляется, на вкладке Explained variance нажмите кнопку Scree plot.

Из построенного графика видно, что в соответствии с этим критери­ем можно пытаться выделить 2 или 3 фактора.

 

 

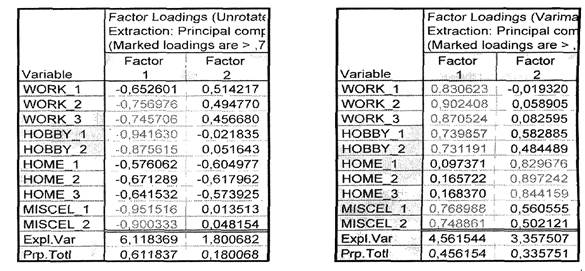
Различные методы выделения факторов расположены на вкладке Advanced окна Define Method of Factor Extraction и объединены в группу опций под заго­ловком Extraction method (метод выделения). Как говорилось в математическом анонсе, в зависимости от критерия оптимальности возможен анализ либо мето­дом Principal components (методом главных компонент), либо одним из методов, объединенных в группу Principal factor analysis (анализ главных факторов).

В группе Principal factor analysis предусмотрены следующие методы:

• Communalities = multiple R**2 (общности равны квадрату коэффициента множественной корреляции);

• Iterated Communalities (MINRES) (итеративные общности или минималь­ные остатки);

• Maximum likelihood factors (максимальное правдоподобие);

• Centroid method (центроидный метод);

• Principal axis method (метод главных осей).

Выберите опцию Principal components. Чтобы лучше понять основные моменты факторного анализа, предположите, что неизвестны критерии определения числа факторов, и поэтому начните анализ с максимального числа факторов. Сохраните значения максимального числа факторов — 10 и минимального собственного зна­чения — 0 (если собственное значение не будет установлено в 0, то количество вы­деленных факторов не будет равняться 10).

Щелкните кнопкой ОК, и на экране появится уже знакомое окно Factor Analysis Results. В верхней информационной части окна указаны:

• Number of variables (число анализируемых переменных);

• Method (метод анализа);

• log(10) determination of correlation matrix (десятичный логарифм детерми­нанта корреляционной матрицы);

• Number of factor extraction (число выделенных факторов);

• Eigenvalues (собственные значения). В нижней части окна находятся функ­циональные кнопки, позволяющие всесторонне численно и графически просмотреть результаты анализа.

Нажмите кнопку Summary. Factor loadings (итоги, факторные нагрузки), на рис. 14.6 приведен фрагмент таблицы с факторными нагрузками — корреля­циями между переменными и выделенными факторами.

 

 

Из таблицы видно, что первому и второму факторам (Factor f, Factor 2) соот­ветствуют большие значения коэффициентов корреляции, чем остальным факто­рам. Причем с увеличением номера фактора значения коэффициентов корре­ляции стремительно уменьшаются. При правильно выбранном количестве факторов таблицы факторных нагрузок должны выявлять закономерности, проявляющиеся в следующем. Факторные нагрузки должны объединять пере­менные в группы, для которых коэффициенты корреляции с факторами при­нимают булыние значения по одной группе и меньшие значения по другой.

Из сказанного следует нецелесообразность рассмотрения всех десяти факто­ров. Воспользуйтесь результатами этой таблицы, критерием Кэттеля, крите­рием Кайзера и назначьте число факторов — 2.

Из фрагмента таблицы результатов, приведенного на рис. Б, видно, что есть некоторая закономерность в значении факторных нагрузок, а именно группе пе­ременных WORK соответствуют булыиие значения коэффициентов корреляции с фактором 1, чем с фактором 2. Аналогичные данные получим для групп пере­менных HOBBY и MISCEL. Но в такой форме выявленные закономерности труд­но проинтерпретировать.

Чтобы получить интерпретируемое решение, надо применить повороты осей, которые достигаются вращением факторов. Как уже говорилось, бели простран­ство общих факторов найдено, то с помощью поворота системы координат в принципе можно получить бесчисленное множество решений. Конечно, такое количество решений — абсурд. Важно найти интерпретируемое решение. Про­грамма предлагает несколько способов вращения:

• Varimax row (варимакс исходных);

• Varimax normalized (варимакс нормализованных);

• Biquartimax raw (биквартимакс исходных);

• Biquaitimax normalized (биквартимакс нормализованных);

• Quartimax raw (квартимакс исходных);

• Quartimax normalized (квартимакс нормализованных);

• Equamax raw (эквимакс исходных);

• Equamax normalized (эквимакс нормализованных).

Метод варимакс предназначен для максимизации дисперсий квадратов исход­ных факторных нагрузок по переменным для каждого фактора, что эквивалентно максимизации дисперсий в столбцах матрицы квадратов исходных факторных нагрузок.

Целью метода биквартимакс является одновременная максимизация суммы дисперсий квадратов исходных факторных нагрузок по факторам и максимиза­ция суммы дисперсий квадратов исходных фактоных нагрузок по переменным. Это эквивалентно одновременной максимизации дисперсий в строках и столбцах матрицы квадратов исходных факторных нагрузок.

Метод квартимакс означает максимизацию дисперсий квадратов факторных нагрузок по факторам для каждой переменной, что эквивалентно максимизации дисперсий в строках матрицы квадратов исходных факторных нагрузок.

Метод эквимакс можно рассматривать как взвешенную смесь вращения по ме­тодам варимакс и квартимакс, что эквивалентно одновременной максимизации дисперсий в строках и столбцах матрицы квадратов исходных факторных нагру­зок. Однако в отличие от вращения по методу биквартимакс относительный вес, назначенный критерию варимакс при вращении, равен количеству факторов, де­ленному на 2.

Дополнительный термин normalized (нормализованные) в названии методов указывает на то, что факторные нагрузки в процедуре нормализуются, т.е. делят­ся на корень квадратный из соответствующей общности. Термин raw (исходные) показывает, что вращаемые нагрузки не нормализованы.

В поле Factor rotation окна Factor Analysis Results на вкладке Quick выбери­те метод поворота осей, например Varimax raw, и щелкните по Summary. Из фраг­мента таблицы факторных нагрузок (рис. Б) следует, что Factor 1 имеет высо­кие факторные нагрузки по переменным WORK и низкие по переменным НОМЕ, a Factor 2 — наоборот: низкие по переменным WORK и высокие по переменным НОМЕ. При этом факторные нагрузки, соответствующие переменным групп HOBBY и MISCEL, принимают промежуточные значения. Это и означает, что вы­деленные два фактора наилучшим образом характеризуют данные.

Выявление и интерпретация закономерностей в таблицах факторных нагру­зок — достаточно трудоемкий процесс. Процедура значительно упрощается, если использовать графическое представление факторных нагрузок. Нажмите кнопку Plot of factor loadings (двумерный график нагрузок). График, представленный на рис. В, иллюстрирует соотношение между факторами и группами перемен­ных. Видно, что группа переменных WORK занимает на плоскости крайнее левое верхнее положение, а группа переменных НОМЕ — крайнее правое нижнее поло­жение. Следовательно, Factor 1 отвечает за удовлетворение, получаемое на работе, a Factor 2 измеряет удовлетворенность домашней жизнью. Поэтому можно сде­лать вывод, что общая удовлетворенность исследуемой группы людей, в основ­ном, определяется двумя факторами — удовлетворенностью работой и удовле­творенностью домом.

 

В

Б

(Г)

 

В диалоге Factor Analysis Results перейдите на вкладку Scores (рис. Г)» Нажмите кнопку Factor Score coefficients, откроется таблица с коэффициентами линейных уравнений регрессий (рис. Д), по которым программа посчитает значения факторов для каждого наблюдения (респондентов).

Нажмите кнопку Factor Scores, появится таблица (рис. Е), в которой ото­бражены значения факторов для каждого респондента. По этим значениям можно судить об отношении респондентов к Factor 1 и Factor2. Положительное значение фактора соответствует позитивному отношению респондента, а отрицательное — негативному.

 

 

	Г Д

 

 

Величина положительного фактора соответствует силе предпочтения данного фактора (для отрицательного — наоборот). Таким образом, процедура редукции данных позволила выделить два значимых фактора — Factor 1 и Factor 2 и сокра­тить число переменных с 10 до 2.