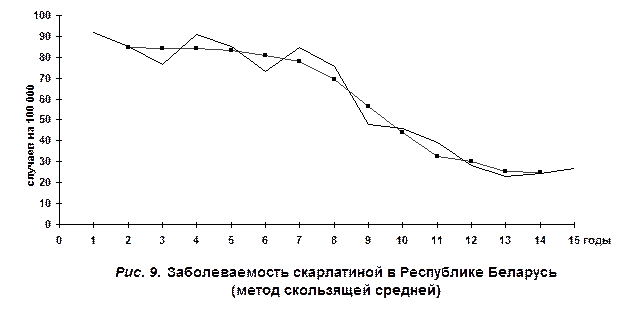
Заболеваемости скарлатиной в Республике Беларусь
Метод удлинения периодов применяется для усреднения резких отклонений в величинах динамических рядов в отдельные годы. С этой целью вычисляют средние арифметические величины, и полученные показатели наносят на линейную диаграмму (табл. 5, рис. 8). При решении вопроса о числе объединяемых периодов исходят главным образом из оценки исследователя. Обычно укрупняемый период включает 2-3 года. Однако при использовании данного метода теряется часть сведений о теоретически ожидаемых величинах. Например, при 3-летнем укрупнении теряются сведения за 2 года – первый и последний. С помощью метода скользящей средней тенденцию эпидемического процесса представляют последовательной серией сплетающихся средних. Эти теоретически ожидаемые величины получают в результате усреднения данных за 2-3 соседних года (табл. 5, рис. 9). Например, первая средняя при 3-летнем периоде усреднения относится ко 2-му году и определяется по формуле: . Вторая средняя определяется по формуле:
и относится к 3-му году и т.д. При использовании данного метода также теряется часть сведений, а при выборе числа лет осреднения немалую роль играет субъективизм исследователя. Метод наименьших квадратов также используют с целью устранения влияния временно действующих причинных факторов и выявления тенденции эпидемического процесса, обусловленную воздействием только постоянных факторов. Тенденцию развития легче всего можно выразить линией, максимально близкой к фактическим данным, что достигается методом наименьших квадратов. Он так называется потому, что сумма возведенных в квадрат разностей фактических ( При выборе функции для описания тенденции динамического ряда желательно опираться на логические представления о характере связи между изменениями уровня заболеваемости и степени активности определяющих его факторов.
При анализе заболеваемости за особенно длительные периоды могут возникнуть затруднения с подбором просто интерпретируемых функций. Связано это, как правило, с наличием длинноволновой периодичности в процессе. В таком случае анализируемый период можно разделить на интервалы и оценить их раздельно. Причем в период, взятый для наблюдения, эпидемический процесс не должен был подвергаться грубым вмешательствам в его ход, существенно изменяющим многолетнюю динамику. Одним из доступных методов определения тенденции эпидемического процесса является метод выравнивания по уравнению линейной зависимости. Он используется, как уже отмечалось, в случае равномерного изменения степени влияния на заболеваемость постоянно действующих факторов. В частности, метод прямолинейного выравнивания (сокращенный метод) позволяет представить тенденцию эпидемического процесса в виде прямой (парабола I порядка), описываемой уравнением линейной зависимости:
где I T – теоретически ожидаемые уровни (показатели) заболеваемости за каждый год периода наблюдения; Неизвестные параметры
где Значение Если в ряду нечетное число вариант, за начальный год (
Отсюда следует, что:
При четном числе периодов нет центрального члена ряда, который можно было бы принять за начальный. В таком случае за начальный период считают тот, который находится между двумя центральными членами ряда, т.е. минимальный промежуток времени, являющийся единицей измерения, равен 1/2 года. Тогда интервал между двумя соседними годами будет равен двум условным единицам. Пример такой ситуации приведен в табл. 6. Таблица 6 Определение интервала четного динамического ряда
В данном случае величины х представляют условную нумерацию не периодов, а целых лет. При этом S Параметр b обозначает на сколько снижаются или увеличиваются теоретически ожидаемые величины в течение единицы времени и называется коэффициентом регрессии даже при положительном значении. Пример расчета многолетней динамики заболеваемости и ее тенденции приведен в табл. 7. Многолетнюю эпидемическую тенденцию (рис. 10) характеризуют по ее направленности и скорости изменений показателей динамического ряда. Направление тенденции многолетней динамики заболеваемости определяется знаком при коэффициенте b. Если он положительный («+»), значит имеет место тенденция к росту заболеваемости, т.е. усиливаются активность постоянных факторов и их влияние на заболеваемость. Если знак b отрицательный («-»), проявляется тенденция к снижению заболеваемости. О скорости изменения ряда и степени выраженности тенденции судят по показателям среднего темпа роста и прироста заболеваемости (Т р и Т пр). Таблица 7 Многолетняя эпидемическая тенденция заболеваемости вирусным гепатитом А населения Республики Беларусь по параболе 1-го порядка
Средний темп прироста отражает на сколько процентов в год в среднем за изучаемый период изменяется заболеваемость, обусловленная постоянно действующими факторами. Значение среднего темпа прироста (Т пр) определяют по формуле:
или Средний темп роста показывает, сколько процентов в год по отношению к предыдущему году составляет заболеваемость, обусловленная постоянно действующими факторами и рассчитывается по формуле: Т р = Т пр + 100%. Средний темп изменения динамического ряда оценивается по следующим критериям. а) при Т прот 0 до б) при Т пр от в) при Т пр от Достоверность многолетней эпидемической тенденции наиболее часто оценивается с помощью распределения Пуассона или критерия «t» Стъюдента. Оценка достоверности по распределению Пуассона выявленного прироста (снижения) осуществляется путем сравнения доверительных границ теоретических показателей заболеваемости (I T) первого и последнего годов наблюдений в определенной последовательности. Вначале находят доверительные интервалы через значения абсолютного числа случаев заболеваний, которые определяют на основании теоретических показателей 1-го и последнего годов наблюдений и численности населения в соответствующие годы.
Для полученных абсолютных значений от 0 до 50 определяют верхнюю и нижнюю доверительные границы по таблице распределения Пуассона (приложение 2). Если А > 50, то доверительные границы рассчитывают по следующим формулам: Аmax = A +1,96 Аmin = A- 1,96 Далее определяют интенсивные показатели полученных доверительных границ теоретических показателей по формулам:
где N – численность населения. Тенденцию к росту считают достоверной, если верхняя доверительная граница теоретического показателя 1-го года наблюдений меньше нижней доверительной границы теоретического показателя последнего года наблюдений: Тенденцию к снижению считают достоверной, если нижняя доверительная граница теоретического показателя 1-го года наблюдений больше верхней доверительной границы теоретического показателя последнего года наблюдений: Если тенденция динамического ряда стабильная, достоверность ее не оценивают. Если же полученные параметры уравнения тенденции оказываются статистически недостоверными, то динамический ряд можно считать относительно стабильным. В данном случае, а также при истинной стабилизации процесса для характеристики ряда вычисляют показатели среднего уровня. Для оценки достоверности по критерию «t» Стъюдента, т.е. по достоверности различия между теоретическими показателями первого и последнего годов наблюдений в динамическом ряду, прежде всего необходимо определить данный критерий:
где d=p 1- p 2 – разность двух показателей; где p 1 и р 2 – теоретические показатели первого и последнего годов;
где р – показатель, кратный 100 000; q = 100 000; N – численность населения. Полученный результат критерия «t» Стъюдента следует сравнить с табличным его значением при числе степеней свободы n=(n 1 +n 2 )- 2. В данном случае n=N (численность населения в анализируемом году). Соответственно для n>;30 критерий «t» Стъюдента при уровне доверия 95,0% равен 1,96 (приложение 6). При уровне доверия 95% табличное значение критерия «t» Стъюдента составляет 1,96 (число степеней свободы >30). Если рассчитанный показатель выше или равен табличному значению при уровне доверия 95%, то различия сравниваемых показателей достоверны, показатели статистически значимо различаются. Если различия сравниваемых показателей недостоверны, то динамический ряд можно считать относительно стабильным. Анализ многолетней динамики заболеваемости при отсутствии прямолинейной тенденции Для реальной динамики эпидемического процесса не всегда характерна прямолинейная тенденция. Выбор функции, описывающей динамический ряд, зависит от характера изучаемого явления и полученной кривой многолетней динамики. При выборе данной функции желательно опираться на логические представления о характере связи между изменениями уровня заболеваемости и определяющих его факторов. Для этого необходимо знать, когда на протяжении анализируемого периода имела место перестройка в том или ином элементе социально-экономической организации населения, способная вызвать существенные изменения в проявлениях эпидемического процесса. Вспомогательным методом, позволяющим оценить точность выравнивания (аппроксимации) динамического ряда, является метод расчета величины достоверности аппроксимации (R2 колеблется от 0 до 1,0). Чем ближе к 1,0 величина достоверности аппроксимации многолетней эпидемической тенденции, тем точнее она соответствует кривой многолетней динамики заболеваемости. Рассмотрим непрямолинейное выравнивание динамического ряда по параболе 2-го порядка. Парабола – одна из элементарных кривых. Параболой 1-го порядка является прямая линия. Парабола 2-го порядка выражается следующим уравнением:
где а – коэффициент, отражающий начальную скорость динамики эпидемического процесса; b и с – постоянный прирост (снижение) уровня показателей во времени. Для определения неизвестных коэффициентов а, в и с используется система 3 уравнений:
Напомним, что
Для определения теоретических показателей по функции параболы 2-го порядка аналитическую табл. 7 необходимо дополнить графами х 4, x 2 I, I T2 (табл. 8), где х – интервал динамического ряда, I T– теоретический показатель заболеваемости по параболе 1-го порядка, I T2 – теоретический показатель заболеваемости по параболе 2-го порядка. Сумму полученных производных подставляют в формулы для поиска неизвестных коэффициентов:
Таким образом, a = 15,83557; b = 0,00267; с = - 0,14387. На основании полученных данных определяют теоретические показатели заболеваемости для каждого года ( Таблица 8
|

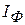 )
)

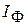 ) и теоретически ожидаемых (
) и теоретически ожидаемых (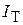 ) значений наименее велика, т. е.,
) значений наименее велика, т. е., 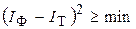 . В каждом отдельном случае этому условию соответствует только одна линия. Таким образом, метод наименьших квадратов можно считать наиболее объективным методом выявления тенденции эпидемического процесса, в связи с чем его рекомендуется широко применять при обработке результатов эпидемиологических исследований.
. В каждом отдельном случае этому условию соответствует только одна линия. Таким образом, метод наименьших квадратов можно считать наиболее объективным методом выявления тенденции эпидемического процесса, в связи с чем его рекомендуется широко применять при обработке результатов эпидемиологических исследований.

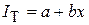 , (1)
, (1)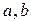 – постоянные коэффициенты;
– постоянные коэффициенты; 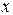 – условная нумерация периодов (интервал динамического ряда), которая указывает на равенство отрезков, определяющих показатели динамического ряда. Обычно выражается целыми числами.
– условная нумерация периодов (интервал динамического ряда), которая указывает на равенство отрезков, определяющих показатели динамического ряда. Обычно выражается целыми числами.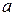 и
и 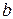 определяются системой уравнений:
определяются системой уравнений: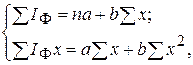
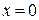 ) принимается медианный, т.е. срединный год в данном ряду. Остальные члены ряда нумеруются в естественном порядке чисел (1, 2, 3, 4 и т.д.), но номера более ранних лет до центрального члена с отрицательным знаком, а после него – с положительным. Значит не только S
) принимается медианный, т.е. срединный год в данном ряду. Остальные члены ряда нумеруются в естественном порядке чисел (1, 2, 3, 4 и т.д.), но номера более ранних лет до центрального члена с отрицательным знаком, а после него – с положительным. Значит не только S 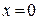 , но и а´Sх=0. В связи с этим приведенная система уравнений упрощается и принимает иной вид:
, но и а´Sх=0. В связи с этим приведенная система уравнений упрощается и принимает иной вид: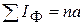 ;
; 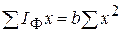 .
.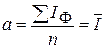 ,
, 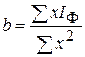 .
.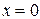 ,
, 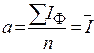 ;
; 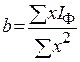 .
.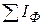 = 218,87
= 218,87
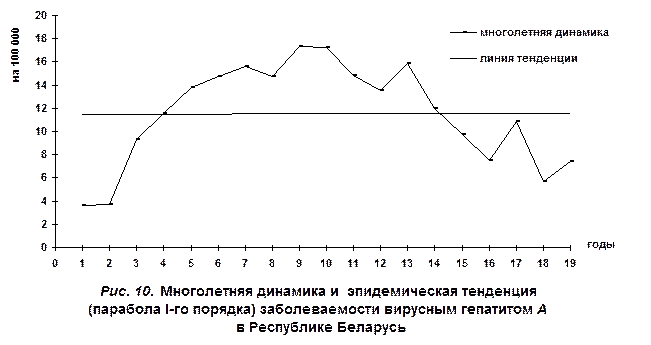
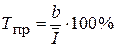 –для нечетного ряда;
–для нечетного ряда;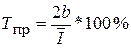 – для четного ряда.
– для четного ряда.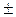 0,99% многолетняя эпидемическая тенденция считается стабильной;
0,99% многолетняя эпидемическая тенденция считается стабильной;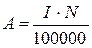 .
.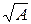 ;
;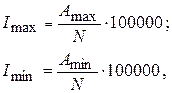
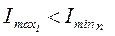 .
.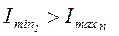 .
.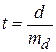 ,
,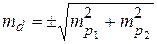 – средняя ошибка разности двух показателей,
– средняя ошибка разности двух показателей,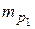 и
и 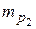 – средние ошибки теоретических показателей первого и последнего годов;
– средние ошибки теоретических показателей первого и последнего годов;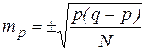 ,
,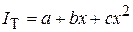 , (2)
, (2)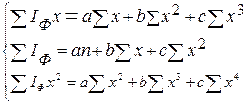 .
.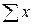 и
и 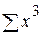 равны 0. Решив данную систему уравнений, получим уравнения для поиска неизвестных коэффициентов:
равны 0. Решив данную систему уравнений, получим уравнения для поиска неизвестных коэффициентов: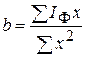 ;
; 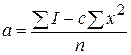 ;
; 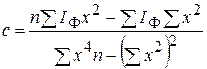 .
.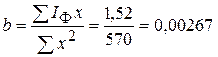 ;
;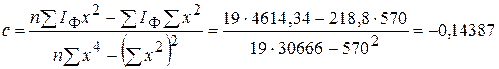 ;
;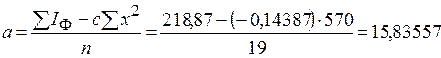 .
.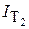 ), подставляя значения коэффициентов а, b и с в формулу
), подставляя значения коэффициентов а, b и с в формулу 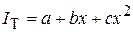 . Результаты записывают в графу 8 табл. 8. Как видно из формулы, значение «а» для всех анализируемых лет постоянно, а произведение bх и сх 2 определяет форму кривой.
. Результаты записывают в графу 8 табл. 8. Как видно из формулы, значение «а» для всех анализируемых лет постоянно, а произведение bх и сх 2 определяет форму кривой.


