Многолетняя эпидемическая тенденция заболеваемости вирусным гепатитом А в городе М.
(по параболе 3-го порядка)
| Годы
| I Ф
| х
| х I Ф
| х 2
| х 2 I Ф
| х 4
| х 3
| х 3 I Ф
| х 6
| I Т
| |
|
|
|
|
|
|
|
|
|
|
| |
| 92,0
| -7
| -644,0
|
| 4508,0
|
| -343
| -31556,0
|
| 84,3
| |
| 85,4
| -6
| -512,4
|
| 3074,4
|
| -216
| -18446,4
|
| 88,6
| |
| 76,7
| -5
| -383,5
|
| 1917,5
|
| -125
| -9587,5
|
| 89,9
| |
| 93,0
| -4
| -372,0
|
| 1488,0
|
| -64
| -5952,0
|
| 88,6
| |
| 85,4
| -3
| -256,2
|
| 768,6
|
| -27
| -2305,8
|
| 85,2
| |
| 73,4
| -2
| -146,8
|
| 293,6
|
| -8
| -587,2
|
| 80,0
| |
| 84,5
| -1
| -84,5
|
| 84,5
|
| -1
| -84,5
|
| 73,5
| |
| 75,8
|
| 0,0
|
| 0,0
|
|
| 0,0
|
| 66,0
| |
| 47,9
|
| 47,9
|
| 47,9
|
|
| 47,9
|
| 58,1
| |
| 55,0
|
| 110,0
|
| 220,0
|
|
| 440,0
|
| 50,0
| |
| 45,0
|
| 135,0
|
| 405,0
|
|
| 1215,0
|
| 42,2
| |
| 28,4
|
| 113,6
|
| 454,4
|
|
| 1817,6
|
| 35,0
| |
| 23,2
|
| 116,0
|
| 580,0
|
|
| 2900,0
|
| 29,0
| |
| 24,3
|
| 145,8
|
| 874,8
|
|
| 5248,8
|
| 24,5
| |
| 26,7
|
| 186,9
|
| 1308,3
|
|
| 9158,1
|
| 21,9
| 
| 916,7
|
| -1544,2
|
| 16025,0
|
|
| -47692,0
|
|
|
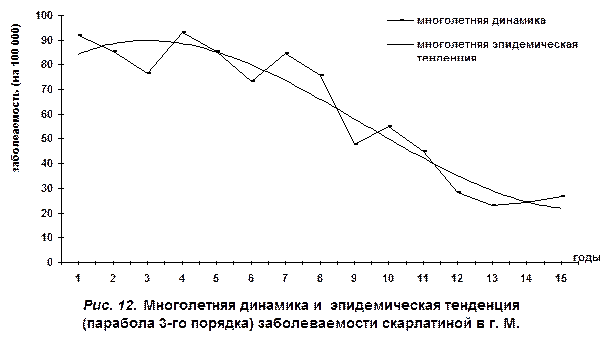
Относительно непрямолинейного выравнивания по экспоненциальной кривой следует сказать, что не всегда тенденцию развития изучаемых явлений можно удовлетворительно выразить прямой или параболой. В тех случаях, когда процесс развивается в геометрической прогрессии, для выравнивания динамических рядов можно использовать так называемую экспоненциальную кривую, описываемую уравнением
 (4). (4).
Технику получения теоретически ожидаемых величин I T, характеризующих степень влияния длительно действующих причинных факторов, можно продемонстрировать на следующем примере.
Имеются данные о заболеваемости (на 100 000 населения). Графический анализ указывает на тенденцию развития, которую можно представить в виде экспоненциальной кривой типа  . Конкретные вычисления, связанные с определением теоретически ожидаемых величин I T, приведены в табл. 10. . Конкретные вычисления, связанные с определением теоретически ожидаемых величин I T, приведены в табл. 10.
На первом этапе работы логарифмируют уравнение

и получают:
 . .
Цель этого – придать уравнению вид, удобный для дальнейшей работы.
На втором этапе составляют систему двух уравнений (при ее решении получают числовые значения параметров а и b):
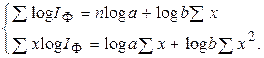
Вполне очевидно, что для решения данной системы необходимо располагать значениями величин  , n, , n, 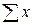 , , 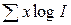 и и  . После условной нумерации периодов, начинающейся с нуля, и определения логарифмов фактических значений производят необходимые действия и находят: . После условной нумерации периодов, начинающейся с нуля, и определения логарифмов фактических значений производят необходимые действия и находят:
log I Ф = 1,0467, x= 105, x log I Ф=42,4181 и x 2=1015.
Подставив значения х, х log I Ф и x 2 в систему уравнений, получим:
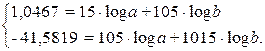
Решив эти уравнения, найдем числовые значения
log a =1,2927 и log b =0,1747.
Подставим их в уравнение и определим значения log I T.
Далее путем антилогарифмирования найдем теоретически ожидаемые значения I T (рис. 13).
Рассмотрим теперь непрямолинейное выравнивание по степенной кривой. В некоторых случаях тенденцию развития изучаемых явлений, независимо от того, восходящее ли оно или нисходящее, нельзя удовлетворительно выразить экспоненциальной кривой типа  , поскольку данное явление изменяется сравнительно плавно. В этих случаях подходит так называемая степенная кривая, которую можно выразить формулой: , поскольку данное явление изменяется сравнительно плавно. В этих случаях подходит так называемая степенная кривая, которую можно выразить формулой:
Таблица 10

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Дренирование желчных протоков Показаниями к дренированию желчных протоков являются декомпрессия на фоне внутрипротоковой гипертензии, интраоперационная холангиография, контроль за динамикой восстановления пассажа желчи в 12-перстную кишку...
Деятельность сестер милосердия общин Красного Креста ярко проявилась в период Тритоны – интервалы, в которых содержится три тона. К тритонам относятся увеличенная кварта (ув.4) и уменьшенная квинта (ум.5). Их можно построить на ступенях натурального и гармонического мажора и минора.
...
Понятие о синдроме нарушения бронхиальной проходимости и его клинические проявления Синдром нарушения бронхиальной проходимости (бронхообструктивный синдром) – это патологическое состояние...
|
Характерные черты немецкой классической философии 1. Особое понимание роли философии в истории человечества, в развитии мировой культуры. Классические немецкие философы полагали, что философия призвана быть критической совестью культуры, «душой» культуры.
2. Исследовались не только человеческая...
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит...
Кран машиниста усл. № 394 – назначение и устройство Кран машиниста условный номер 394 предназначен для управления тормозами поезда...
|
|


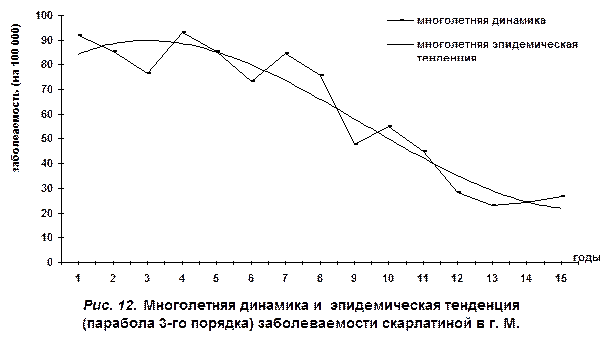
 (4).
(4). .
.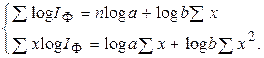
 , n,
, n, 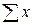 ,
, 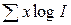 и
и  . После условной нумерации периодов, начинающейся с нуля, и определения логарифмов фактических значений производят необходимые действия и находят:
. После условной нумерации периодов, начинающейся с нуля, и определения логарифмов фактических значений производят необходимые действия и находят: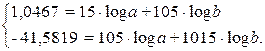
 , поскольку данное явление изменяется сравнительно плавно. В этих случаях подходит так называемая степенная кривая, которую можно выразить формулой:
, поскольку данное явление изменяется сравнительно плавно. В этих случаях подходит так называемая степенная кривая, которую можно выразить формулой:


