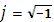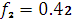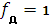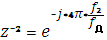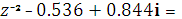Визначення передатної функції цифрового ФНЧ.
Із останнього виразу отримаємо:
Після перетворення отримаємо:
=
Оскільки вільний член знаменника виразу
Для перевірки обчислень впевнимось, що коефіцієнт передачі розрахованого ЦФ рівний
ПОБУДОВА СТРУКТУРНОЇ СХЕМИ ФІЬТРУ
Даний вираз відповідає послідовній формі реалізації цифрового ФВЧ.
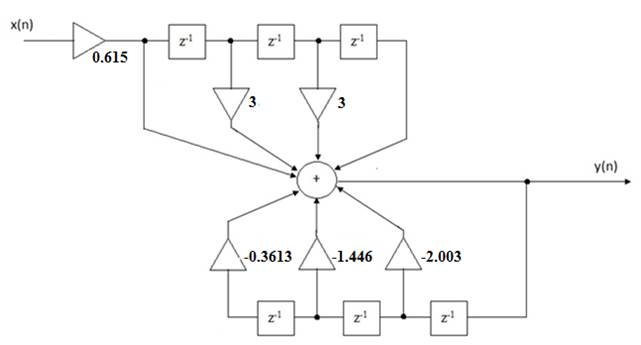
Для отримання форми реалізації цифрового ФВЧ розкриємо дужки в чисельнику і знаменнику даного виразу:
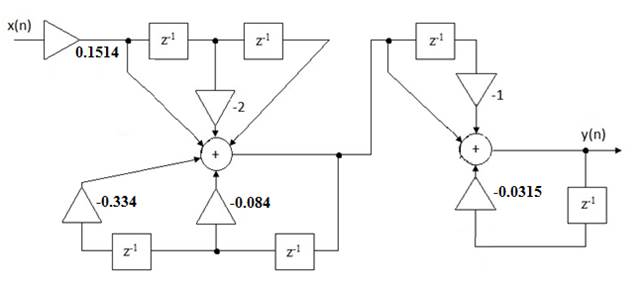
Даний вираз відповідає послідовній формі реалізації цифрового ФНЧ.
Для отримання форми реалізації цифрового ФНЧ розкриємо дужки в чисельнику і знаменнику даного виразу:
ВИСНОВКИ В своїй розрахунковій роботі я розрахувала смуговий фільтр Баттерворта (який є послідовним з’єднанням ФВЧ та ФНЧ) непрямим методом – методом білінійних перетворень. Цей метод заснований на переході від аналогового фільтра-прототипа з передатною функцією K(P) до цифрового фільтра зз передатною функцією H(z). При цьому методі ми вибираємо аналогові нормовані ФВЧ та ФНЧ Баттерворта в якості аналогового прототипу. Шляхом перетворення частот ми отримуємо їх АЧХ. Після цього знаходимо передатні функції аналогових фільтрів, а на їх основі і передатні функції цифрових. На основі отриманих виразів будуємо структурну схему проектуємого СФ.
СПИСОК ВИКОРИСТАННОЇ ЛІТЕРАТУРИ 1. Хеммінг Р.В. Цифрові фільтри. – М.: Радянське радіо, 1980 2. Рабинер Л.Р. Голуд В. Теория и применение цтфровой обработки сигналов. – М.: Мир, 1978 3. Український радянський енциклопедичний словник. У 3-х т. Т. 3. – 2-ге вид. – Київ, 1987
|



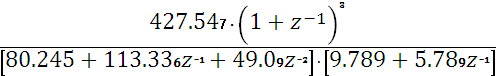
 повинен бути рівним одиниці, розділимо чисельник і знаменник останнього виразу:
повинен бути рівним одиниці, розділимо чисельник і знаменник останнього виразу:
 0,707:
0,707: