Косвенный метод стандартизации
Если в распоряжении исследователя имеются данные о возрастной структуре сравниваемых совокупностей населения, но неизвестны возрастные коэффициенты смертности и нет исходных данных для их расчета, то можно произвести стандартизацию коэффициентов косвенным методом. В этом случае за стандарт принимаются возрастные коэффициенты какого-либо населения, которые можно найти в статистических справочниках. При этом методе стандартизация производится косвенно, т.е. мы задаемся вопросом, каким было бы общее число умерших, если бы возрастные коэффициенты смертности во всех сравниваемых группах были бы одинаковыми и именно такими как в стандарт-населении (т.е. в населении, принятом за стандарт). Это рассуждение можно выразить в виде формулы: M = a М х = a P x m x, или, если эту формулу пересказать словами, она означает, что общее число умерших M равно сумме умерших во всех возрастных группах a М x, которая, в свою очередь, может быть представлена в виде суммы произведений численности населения каждой возрастной группы на соответствующий ей возрастной коэффициент смертности. По условию нам известны возрастные структуры сравниваемых групп населения, но неизвестны их возрастные коэффициенты смертности. Поэтому заменяем неизвестные возрастные фактические коэффициенты смертности произвольно подобранными (из справочника, относящимися к любому населению, о котором мы все же априори знаем, что его повозрастная смертность не слишком отличается от смертности в сравниваемых населениях). Используя возрастные коэффициенты смертности населения, принятого за стандарт, получаем так называемые условные числа умерших, т. е. числа умерших, какими они были бы при условии, что повозрастная смертность во всех сравниваемых группах населения одинакова и такая, как в населении, принятом за стандарт. В виде формулы это можно изобразить таким образом: М 0 = a P x х т х 0, где M 0? условное число умерших, Р х — фактические возрастные структуры сравниваемых населений, и т х 0? возрастные коэффициенты смертности населения, принятые за стандарт. Сравнивая затем фактическое число умерших в каждом населении с соответствующим этому населению условным числом умерших, получаем индекс, показывающий, насколько фактическая повозрастная смертность в сравниваемом населении (или группе населения) отличается от смертности стандарт-населения. Умножая этот индекс на общий коэффициент смертности стандарт-населения (т 0), получаем в итоге стандартизованный коэффициент смертности для каждого сравниваемого населения. Окончательно наши рассуждения удобно выразить следующей формулой:
где т C Т — стандартизованный общий коэффициент смертности; Р х — возрастные группы сравниваемого населения; М — общее число умерших в сравниваемом населении; т х 0 — возрастные коэффициенты смертности населения, принятого за стандарт, и т 0 — общий коэффициент смертности населения, принятого за стандарт. Но расчет самих стандартизованных коэффициентов смертности для проведения сравнений уровней смертности на самом деле вовсе не обязателен. Это, скорее всего, лишь дань привычке, уступка нашему желанию увидеть коэффициенты смертности в привычном виде. Однако эта привычка не безобидна, так как заставляет некоторых аналитиков трактовать величину стандартизованного коэффициента аналогично фактической. В этом случае нередко рассуждают так: «Фактические коэффициенты измеряют процесс неправильно, потому что их величина зависит от особенностей возрастной структуры. А стандартизованные коэффициенты (их величина) отражают уровень демографического процесса правильно, потому что они свободны от влияния возрастной структуры». Между тем величина стандартизованного коэффициента вовсе не характеризует уровень смертности. Сама по себе она — условна, самостоятельного значения не имеет никакого (ведь она во многом зависит от особенностей возрастной структуры стандарт-населения). Поэтому вполне можно ограничиться расчетом индексов, выражающих соотношение фактических и условных чисел умерших, с последующим сравнением между собой уже этих индексов. Представим это рассуждение в виде формулы: J m СТ где все условные обозначения известны из предыдущей формулы. От подобного упрощения расчет станет только точнее (за счет сокращения количества округлений). В качестве примера сравним уровни смертности мужского и женского населения России в 1995 г. [5] (таблица 6.4). Общие коэффициенты смертности мужского и женского населения России в 1995 г. составили соответственно 16,9 и 13,3 ‰. Отсюда определяем, что уровень смертности мужчин выше, чем женщин, на 16,9/13,3 = 1,271, т.е. на 27,1%. Это немало, но с такой разницей можно было бы согласиться. Однако мы догадываемся, что именно в силу более высокой продолжительности жизни женщин по сравнению с мужчинами их возрастная структура в среднем старше аналогичной структуры мужского населения. Стандартизация коэффициентов смертности позволяет устранить (элиминировать) влияние различий возрастной структуры мужского и женского населения на величину общих коэффициентов смертности, так сказать, уравнять их в этом отношении. Окончательный расчет по формуле будет таким: J m СТ = 1197048 / 779467 х 1428193 / 1055541 = 1,536 х 1,353 = 2,078 Результат расчета показывает, что на самом деле смертность мужчин выше, чем смертность женщин, не на 27%, а в 2,1 раза. Это уже явно ничем не оправданная и нетерпимая разница в продолжительности жизни, имеющая далеко идущие и многообразные демографические и другие социальные последствия. В заключение этого раздела хочу обратить внимание на два очень важных обстоятельства, связанных с использованием методов стандартизации коэффициентов. Во-первых, не существует какого-либо формализованного способа выбора (подбора) стандарт-населения. Это делается на основе опыта. Подбирается население — его параметры (возрастная структура при прямом методе стандартизации — или возрастные коэффициенты смертности — при косвенном методе), — о котором априори известно, что оно по этим параметрам схоже с теми населениями, уровни демографических процессов которых (любых, не обязательно только смертности) сравниваются между собой. Если сравниваются населения с резко различающимися возрастными структурами, то параметры стандарт-населения выбираются таким образом, чтобы они были средними между параметрами сравниваемых населений (предполагаемых или известных за другие годы и т.п.). Таблица 6.4
Во-вторых, считаю необходимым повторно предупредить читателя о том, что сама по себе величина стандартизованных коэффициентов носит условный характер, зависит от выбранного стандарта (стандарт-населения), поэтому она не имеет никакого самостоятельного значения. Имеет значение только разница между стандартизованными коэффициентами, которая в идеале остается неизменной при любом стандарте (небольшая разница в результатах может быть следствием грубости расчета, округлений цифр либо не очень удачного выбора стандарт-населения, если оно по своим характеристикам очень сильно отличается от сравниваемых населений). Вероятностные таблицы смертности (чаще называемые просто таблицами смертности) Это самый совершенный инструмент для анализа состояния и тенденций уровня смертности. Они представляют собой систему взаимосвязанных показателей, характеризующих изменение вероятности смерти по мере увеличения возраста людей, или, напротив, изменение вероятности дожития до некоторого возраста, а также среднюю продолжительность жизни некоторого поколения родившихся. Иначе говоря, таблицы смертности описывают последовательность и скорость вымирания поколения. Показатели (колонки) таблиц смертности:
В таблицах смертности принимают первоначальную численность поколения (число родившихся, основание или корень таблицы смертности) неизменной во времени и равной единице и прослеживают, как с переходом от возраста к возрасту, от 0 до предельного возраста (100 лет или 100 с небольшим) первоначальная совокупность поколения родившихся убывает в результате смерти от 1 до 0. Отсюда следует, что в таблицах смертности все числа, кроме числа родившихся, равного 1, меньше 1, т. е. дроби. Чтобы избежать большого количества дробных чисел, число родившихся (основание таблицы) в практических расчетах принимают равным 100000 или 10000, в зависимости от желаемой значности (точности) расчетов. Но не менее 10000. Различают таблицы полные и краткие. В полных таблицах возрастные интервалы равны одному году, в кратких — пяти годам. Целесообразно рассмотреть взаимосвязи показателей таблиц смертности на примере полных таблиц. В них с переходом от возраста «х» к возрасту «х + 1» число доживающих l x будет последовательно уменьшаться на величину числа умирающих в возрасте «х», т.е. d x. Математически эта связь выглядит следующим образом: L x +1 = l x – d x (6.5.1) Если проследить эту последовательность (порядок) вымирания поколения, начиная с основания таблицы смертности, то она будет выглядеть следующим образом: l 0 = 1 или 10000 или чаще 100000 – d 0 = l 1 – d 1 = l 2 – d 2 = l 3 и т.д. В общем виде эту последовательность можно записать так: l x +1 = l x – d x (для полных таблиц) и l х+п = l x – d x + n, где п — длина возрастного интервала. Каждый родившийся рано или поздно умирает, и в конечном счете число умерших (из каждого поколения, численность которых мы определили заранее) составит l 0, т. е. число родившихся, или
где w –1 — предельный возраст, до которого доживает последний человек из поколения родившихся. Формула (6.5.1) может быть использована в различных перестановках, к примеру: l x = l x +1 + d x; d x = l x – l x +1, и т.д. Вероятность смерти в возрасте «х» (в возрастном интервале от «х» до «х + 1»)? q x — определяется в соответствии с правилами теории вероятностей как отношение числа умирающих в возрасте «х» – d x к числу доживающих до этого возраста, т.е. l z. В виде формулы эта связь выглядит так:
Из формулы хорошо видно, что вероятность смерти q x можно интерпретировать и как долю умирающих в возрасте «х» из числа доживающих до начала возрастного интервала «х». Напротив, вероятность дожития до возраста «х + 1» — р х для тех, кто дожил до возраста «х» (до начала возрастного интервала «х»), будет определяться как отношение числа доживающих до возраста «х + 1» к числу доживших до возраста «х» (до начала возрастного интервала «х»). Запишем эту связь в виде формулы:
Отсюда можно так же, как и в предыдущей формуле, видеть, что вероятность дожития есть не что иное, как доля переживающих возраст «х» из числа доживающих до его начала. Формулы (6.5.2) и (6.5.3) так же, как и (6.5.1), используются в виде различных преобразований, например: l x +1 = l x р х; d x = l x q x b и т. д. Поскольку мы рассматриваем смертность, то в пределах одного возрастного интервала возможна только единственная альтернатива: либо пережить этот интервал и благополучно отметить следующий день рождения, либо, увы, не дожить до него. Иначе говоря, сумма вероятностей дожития до следующего возраста либо умереть, не дожив до него, равна единице, что можно изобразить в виде формулы: q x + р х = 1. (6.5.4) Эта простейшая формула оказывается, однако, очень полезной, так как, зная одну из двух вероятностей, всегда легко найти вторую (вычитанием из единицы). Начав прослеживать закономерное уменьшение чисел доживающих с основания таблицы смертности, замечаем вскоре, что: l 1 = l 0 p 0. Если основание таблицы l 0 = 1, то, естественно, l 0 в формуле можно опустить, и она примет вид: l 1 = р 0. Далее, следуя той же логике: l 2 = l 1 p 1. Подставим вместо l 1 его значение из предыдущей формулы (l 1 = р 0). Получим: l 2 = р 0 p 1. Затем: l 3 = l 2 р 2 = p 0 p 1 p 2 и т.д. Отсюда, кстати, видно, что число доживающих — нечто иное, как произведение вероятностей дожития, или, иначе говоря, оно само — тоже вероятность, вероятность для новорожденного дожить до возраста «х». В обобщенном виде эту связь можно записать и так: l x = p 0 p 1 p 3 x ………. x p x-1. (6.5.5) Поскольку в практических расчетах основание таблицы смертности принимается равным не 1, а 10000 и чаще всего 100000, то l 0 опускать не приходится и формула (6.5.5) выражается в следующем виде: l x = l 0 p 0 p 1 p 2 p 3 x ………. x p x-1. Здесь, пожалуй, самое время сказать, что в таблицах смертности нет ни одного доживающего или умирающего. Вообще — ни одного человека. Одна смерть в чистом виде. Одни вероятности и доли. В этом их большое преимущество перед другими измерителями уровня смертности, поскольку при отсутствии человека нет и зависимости показателей таблиц смертности от возрастной структуры населения. Наименования «числа доживающих», «числа умирающих» — опять же условные наименования, не более того.
Рис.6.2. Вероятность умереть qx для мужского и женского населения СССР, 1986—1987 гг. Последовательность изменений чисел доживающих l x графически представляет собой линию дожития,характеризующую порядок вымирания поколения. Чем ниже уровень смертности, чем большая доля родившихся (поколения) доживает до старших возрастов, тем более выпуклой формы будет кривая дожития (см. рис.6.4). Числа живущих. В таблицах смертности числа доживающих показывают долю остающихся в живых к началу каждого следующего года возраста, то есть к возрасту «x» лет остается в живых часть поколения l x, к возрасту «х + 1» — часть l x +1, и т.д. Однако на самом деле при переходе от одного возраста к следующему численность поколения убывает непрерывно, поэтому число живущих в возрасте «х» есть некоторая средняя величина между значениями чисел доживающих l x и l x +1. Если разбить каждый год возраста на предельно малые промежутки времени и с помощью дифференциального исчисления определить средние величины живущих в каждом таком мельчайшем интервале, то изменение чисел живущих определяется путем интегрирования таких средних. В реальности интегрирование заменяется суммированием.
Рис.6.3. Число умирающих dx мужчин и женщин СССР, 1986—1987 гг. На практике обычно мы не располагаем значениями чисел доживающих l x, для более дробных возрастных интервалов, чем год. Поэтому для средних возрастов, в которых число доживающих изменяется почти прямолинейно, число живущих рассчитывается как обычная средняя арифметическая величина из двух чисел доживающих, на начало и конец возрастного интервала, т. е.:
На тех же участках кривой дожития, где ее кривизна значительна, число живущих определяют по формуле, учитывающей эту кривизну:
где d x — число умирающих в таблицах смертности; т х — возрастные коэффициенты смертности того же населения, для которого строились таблицы смертности. Обычно по формуле (6.5.7) рассчитывают число живущих для всех участков кривой дожития, кроме самых первых детских возрастов, для которых используются специальные формулы (мы познакомимся с ними позднее, при построении краткой таблицы смертности). Средняя ожидаемая продолжительность жизни. Число живущих можно трактовать также и как число человеко-лет, прожитых всем поколением родившихся в интервале возраста «x». Тогда, следовательно,
Рис.6.4. Линии дожития lx мужского и женского населения СССР, 1926—1927, 1958—1959, 1986—1987 гг. поколение родившихся l 0 проживет на первом году жизни (т.е. в возрасте 0 лет) L 0 лет, на 2-м году — L i лет, на 3-м — l 2 лет и т.д., а всего:
где Т 0 — число человеко-лет, которое предстоит прожить данному поколению родившихся. Если эту сумму человеко-лет разделить на первоначальную численность поколения, т.е. на число родившихся l 0, то получим очень важный социальный показатель, который называется показателем средней ожидаемой продолжительности жизни. Средняя ожидаемая продолжительность предстоящей жизни [6] — это число лет, которое проживет один человек в среднем из данного поколения родившихся при условии, что на всем протяжении жизни этого поколения смертность в каждой возрастной группе будет оставаться неизменной на уровне расчетного периода. Продолжительность предстоящей жизни рассчитывается для новорожденных (или иначе говорят — ожидаемая продолжительность жизни при рождении) и для достигших некоторого возраста «х». В виде формул расчет обеих средних можно представить следующим образом. Для новорожденных:
Поскольку при расчете средней продолжительности предстоящей жизни для новорожденных основание таблицы смертности l 0 = 1, его можно опустить, и окончательно этот показатель выражается в виде суммы чисел живущих в жизненном интервале от рождения поколения до его полного исчезновения. Для людей, достигших определенного возраста «x», расчет отличается лишь тем, что число доживающих до возраста «х», в знаменателе дроби уже меньше 1 и его опускать нельзя.
|

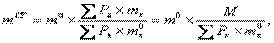 (6.8)
(6.8)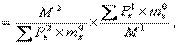 (6.9)
(6.9)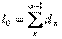
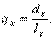 (6.5.2)
(6.5.2) (6.5.3)
(6.5.3)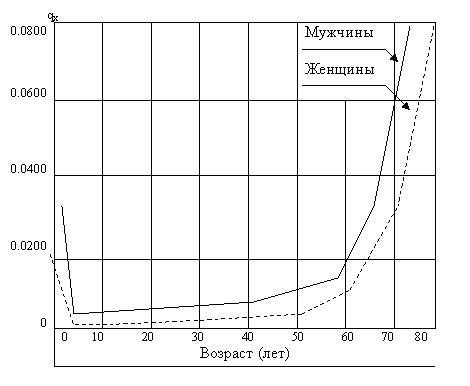

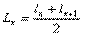 (6.5.6)
(6.5.6) (6.5.7)
(6.5.7)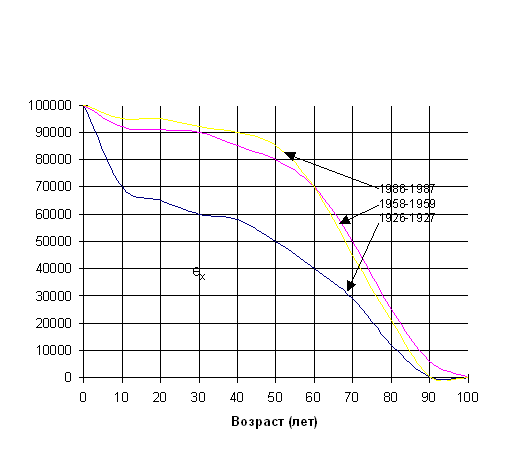
 (6.5.8)
(6.5.8) (6.5.9)
(6.5.9)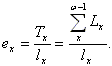 (6.5.10)
(6.5.10)


