Расчет кратких таблиц смертностиДля анализа состояния и тенденций уровня смертности чаще всего бывает достаточным использование кратких таблиц смертности, т.е. по пятилетним возрастным интервалам. Для их построения необходимо располагать пятилетними возрастными коэффициентами смертности или данными для расчета таких коэффициентов. Обычно достаточно рассчитать лишь одну колонку таблиц, l x, q x или p x, а все остальные колонки, кроме L x, рассчитываются на основе взаимосвязей показателей таблиц смертности, представленных выше. Для перехода от возрастных коэффициентов смертности т х к вероятностям смерти q x используется обычно одна из двух формул:
где q x — вероятность смерти в возрасте «х»; т х — возрастной коэффициент смертности; n — длина возрастного интервала. Все остальные формулы показаны выше. Построим для примера краткие таблицы смертности мужского населения России за 1995 г. и рассмотрим алгоритм расчета (см. таблицу 6.5). 1. Из двух методов расчета по формулам (6.5.10) и (6.5.1 1) выберем второй метод — по показательной функции, потому, что она лучше, чем первая, учитывает кривизну изменения чисел доживающих l x. При этом вместо колонки вероятностей смерти q x будем рассчитывать колонку ее дополнения до единицы, т.е. вероятность дожития до следующего возраста, p x. Таким путем мы избежим большого числа вычитаний из единицы. 2. Но сначала нужно возрастные коэффициенты смертности разделить на 1000 (т.е. перевести их из промилле в доли единицы) и перемножить на длину соответствующих возрастных интервалов. Для первого возрастного интервала 0 лет множитель будет равен 1, для второго — 1 — 4 года — 4, для остальных интервалов — 5. 3. Затем, возводя основание натурального логарифма «е» в отрицательную степень, равную произведению возрастного коэффициента смертности на длину возрастного интервала, находим значения колонки вероятностей дожития p x (колонка 3 в таблице 6.5). 4. Следующая колонка — чисел доживающих «l x». Первое значение числа доживающих для возраста 0 лет — основание таблицы смертности 100000 (константа, которую всегда нужно помнить). Умножив 100000 на число доживающих p 0, получаем число доживающих l1, умножив l 1 на p 1, получаем l 2, и так — все значения колонки чисел доживающих до возраста «85 лет и старше». 5. Затем рассчитываем значения колонки d x как разность между соседними числами доживающих, т.е. 100000 – l 0 = d 0; l 1 – l 2 = d 1, и т.д. 6. Далее рассчитываем числа живущих. Для всех возрастных интервалов, кроме первых двух ранних детских, числа живущих рассчитываются по формуле L x = dx / т х. Для первых двух возрастных интервалов — 0 и1—4 — числа живущих определяются иначе ввиду резкой кривизны изменения линии дожития на этом участке. Так число живущих в возрасте 0 лет определяется уравнением L 0 = l 0 - 2 / 3 d x. Число живущих в следующем детском возрастном интервале 1—4 года определяется из следующего уравнения 4 L 1 = 1,704 l 1 + 2,533 l 5 - 0,237 l 10. Число живущих в так называемом открытом возрастном интервале — 85 лет и старше — определяется по формуле L 85+ = l 85 / m 85+. Поскольку все дожившие до 85 лет раньше или позже умрут после этого возраста, d 85+ = l 85. Таблица 6.5
Таблицы 6.5 (продолжение)
7. Значения колонки чисел живущих в возрастах старше «x» - Т х — получаются суммированием чисел живущих L x с последовательным наращиванием суммы от конца ряда к началу. 8. Теперь путем деления чисел живущих в возрасте «х» лет и старше — T x — на соответствующие числа доживающих — l x — определяется средняя ожидаемая продолжительность предстоящей жизни — е x (колонка 8). 9. В колонке 9 показаны значения средней продолжительности жизни для всех возрастов, рассчитанные Госкомстатом России, а в колонке 10 — разность между значениями средней продолжительности жизни, рассчитанными нами по кратким таблицам смертности и сотрудниками госстатистики — по полным таблицам. Как видим, разница невелика, можно даже сказать — несущественна.
|
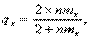(6.5.11)
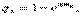(6.5.12)
