Аксиома непрерывности — это единственная аксиома современной теории вероятностей, относящаяся именно к ситуации бесконечного числа случайных событий. Обычно в современной теории вероятностей вероятностным пространством называется только такое вероятностное пространство  , которое, кроме того, удовлетворяет аксиоме V. Вероятностные пространства в смысле аксиом I—IV Колмогоров предлагал называть вероятностными пространствами в расширенном смысле (у Колмогорова поле вероятностей в расширенном смысле), в настоящее время этот термин употребляется крайне редко. Заметим, что если система событий
, которое, кроме того, удовлетворяет аксиоме V. Вероятностные пространства в смысле аксиом I—IV Колмогоров предлагал называть вероятностными пространствами в расширенном смысле (у Колмогорова поле вероятностей в расширенном смысле), в настоящее время этот термин употребляется крайне редко. Заметим, что если система событий  конечна, аксиома V следуeт из аксиом I—IV. Все модели с вероятностными пространствами в расширенном смысле удовлетворяют, следовательно, аксиоме V. Система аксиом I—V является, непротиворечивой и неполной. Напротив, для бесконечных вероятностных пространств аксиома непрерывности V является независимой от аксиом I—IV.
конечна, аксиома V следуeт из аксиом I—IV. Все модели с вероятностными пространствами в расширенном смысле удовлетворяют, следовательно, аксиоме V. Система аксиом I—V является, непротиворечивой и неполной. Напротив, для бесконечных вероятностных пространств аксиома непрерывности V является независимой от аксиом I—IV.
Так как новая аксиома существенна лишь для бесконечных вероятностных пространств, то почти невозможно разъяснить её эмпирическое значение, например, так, как это было проделано с аксиомами элементарной теории вероятности (I—IV). При описании какого-либо действительно наблюдаемого случайного процесса можно получать только конечные поля — вероятностные пространства в расширенном смысле. Бесконечные вероятностные пространства появляются как идеализированные схемы действительных случайных явлений. Общепринято молчаливо ограничиваться такими схемами, которые удовлетворяют аксиоме V, что оказывается целесообразным и эффективным в различных исследованиях.
Алгебра  событий пространства элементарных событий Ω называется борелевской алгеброй, если все счётные суммы
событий пространства элементарных событий Ω называется борелевской алгеброй, если все счётные суммы
событий xn из  принадлежат
принадлежат  . В современной теории вероятностей борелевские алгебры событий обычно называют σ-алгебрами событий (сигма-алгебрами). Пусть дано вероятностное пространство в расширенном смысле
. В современной теории вероятностей борелевские алгебры событий обычно называют σ-алгебрами событий (сигма-алгебрами). Пусть дано вероятностное пространство в расширенном смысле  . Известно, что существует наименьшая сигма-алгебра
. Известно, что существует наименьшая сигма-алгебра  , содержащая
, содержащая 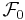 . Более того, справедлива
. Более того, справедлива
Теорема (о продолжении). Определённую на  неотрицательную счётно-аддитивную функцию множеств
неотрицательную счётно-аддитивную функцию множеств 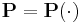 всегда можно продолжить с сохранением обоих свойств (неотрицательности и счётной аддитивности) на все множества из
всегда можно продолжить с сохранением обоих свойств (неотрицательности и счётной аддитивности) на все множества из  и при этом единственным образом.
и при этом единственным образом.
Таким образом, каждое вероятностное пространство в расширенном смысле  может быть математически корректно продолжено до бесконечного вероятностного пространства
может быть математически корректно продолжено до бесконечного вероятностного пространства  , которое в современной теории вероятностей принято называть просто вероятностным пространством.
, которое в современной теории вероятностей принято называть просто вероятностным пространством.

 , которое, кроме того, удовлетворяет аксиоме V. Вероятностные пространства в смысле аксиом I—IV Колмогоров предлагал называть вероятностными пространствами в расширенном смысле (у Колмогорова поле вероятностей в расширенном смысле), в настоящее время этот термин употребляется крайне редко. Заметим, что если система событий
, которое, кроме того, удовлетворяет аксиоме V. Вероятностные пространства в смысле аксиом I—IV Колмогоров предлагал называть вероятностными пространствами в расширенном смысле (у Колмогорова поле вероятностей в расширенном смысле), в настоящее время этот термин употребляется крайне редко. Заметим, что если система событий  конечна, аксиома V следуeт из аксиом I—IV. Все модели с вероятностными пространствами в расширенном смысле удовлетворяют, следовательно, аксиоме V. Система аксиом I—V является, непротиворечивой и неполной. Напротив, для бесконечных вероятностных пространств аксиома непрерывности V является независимой от аксиом I—IV.
конечна, аксиома V следуeт из аксиом I—IV. Все модели с вероятностными пространствами в расширенном смысле удовлетворяют, следовательно, аксиоме V. Система аксиом I—V является, непротиворечивой и неполной. Напротив, для бесконечных вероятностных пространств аксиома непрерывности V является независимой от аксиом I—IV. . Известно, что существует наименьшая сигма-алгебра
. Известно, что существует наименьшая сигма-алгебра  , содержащая
, содержащая 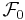 . Более того, справедлива
. Более того, справедлива неотрицательную счётно-аддитивную функцию множеств
неотрицательную счётно-аддитивную функцию множеств 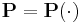 всегда можно продолжить с сохранением обоих свойств (неотрицательности и счётной аддитивности) на все множества из
всегда можно продолжить с сохранением обоих свойств (неотрицательности и счётной аддитивности) на все множества из 


