Независимость событий в совокупности
События из произвольного множества
из попарной независимости событий не следует их независимость в совокупности.
Пусть вероятность события В не зависит от появления события А. Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности: РA (В) = Р (В). (*) если событие В не зависит от события A, то событие A не зависит от события В; это означает, что с в о й с т в о н е з а в и с и м о с т и с о б ы т и й в з а и м н о. Для независимых событий теорема умножения Р (АВ) = Р (А) РA (В) имеет вид Р (АВ) = Р (А) Р (В), (**)
т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий. Равенство (**) принимают в качестве определения независимых событий. Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми. Несколько событий называют попарно независимыми, если каждые два из них независимы. Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С. Для того чтобы обобщить теорему умножения на несколько событий, введем понятие независимости событий в совокупности. Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Например, если события A1, A2, А3, независимы в совокупности, то независимы события A1 и А2, А1 и А3, А2 и A3; А1 и A2A3, A2 и A1A3, А3 и A1A2. Из сказанного следует, что если события независимы в совокупности, то условная вероятность появления любого события из них, вычисленная в предположении, что наступили какие-либо другие события из числа остальных, равна его безусловной вероятности. С л е д с т в и е. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий: Р (А1А2... Аn) = Р (А1) Р (А2)... Р (Аn). 6.Теорема о вероятности суммы событий. Формула полной вероятности. Вероятность гипотез: постановка задачи. Формулы Байеса для вероятностей гипотез. Определение 3.1. Пусть событие А может произойти только совместно с одним из событий Н 1, Н 2,…, Нп, образующих полную группу несовместных событий. Тогда события Н 1, Н 2,…, Нп называются гипотезами . Теорема 3.1. Вероятность события А, наступающего совместно с гипотезами Н 1, Н 2,…, Нп, равна:
где p (Hi) – вероятность i- й гипотезы, а p (A/Hi) – вероятность события А при условии реализации этой гипотезы. Формула (3.1) носит название формулы полной вероятности. Доказательство. Можно считать событие А суммой попарно несовместных событий АН 1, АН 2,…, АНп. Тогда из теорем сложения и умножения следует, что
что и требовалось доказать. Пример. Имеются три одинаковые урны с шарами. В первой из них 3 белых и 4 черных шара, во второй – 2 белых и 5 черных, в третьей – 10 черных шаров. Из случайно выбран-ной урны наудачу вынут шар. Найти вероятность того, что он белый. Решение. Будем считать гипотезами Н 1, Н 2 и Н 3 выбор урны с соответствующим номером. Так как по условию задачи все гипотезы равновозможны, то
|

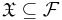 называются независимыми в совокупности, если для любого подмножества событий
называются независимыми в совокупности, если для любого подмножества событий 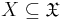
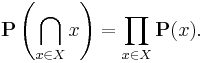
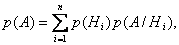 (3.1)
(3.1)
 Найдем условную вероятность А при реализации каждой гипотезы:
Найдем условную вероятность А при реализации каждой гипотезы: 
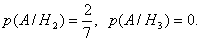 Тогда
Тогда 



