Непрерывные случайные величины. Способы задания непрерывной случайной величины. Плотность вероятности и ее основные свойства.
Определение 4.1. Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причем заранее неизвестно, какое именно. Будем обозначать случайные величины заглавными буквами латинского алфавита (Х, Y,Z,…), а их возможные значения – соответствующими малыми буквами (xi, yi,…). Определение 4.2. Случайная величина называется дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями. Определение 4.3. Случайная величина называется непрерывной, если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток. Определение и свойства функции распределения сохраняются и для непрерывной случайной величины, для которой функцию распределения можно считать одним из видов задания закона распределения. Но для непрерывной случайной величины вероятность каждого отдельного ее значения равна 0. Это следует из свойства 4 функции распределения: р (Х = а) = F (a) – F (a) = 0. Поэтому для такой случайной величины имеет смысл говорить только о вероятности ее попадания в некоторый интервал. Вторым способом задания закона распределения непрерывной случайной величины является так называемая плотность распределения (плотность вероятности, дифферен-циальная функция). Определение 5.1. Функция f (x), называемая плотностью распределения непрерывной случайной величины, определяется по формуле: f (x) = F′;(x), (5.1) то есть является производной функции распределения. Свойства плотности распределения. 1) f (x) ≥ 0, так как функция распределения является неубывающей. 2) 3) Вероятность попадания случайной величины в интервал (а, b) определяется формулой 4) 5) Таким образом, график плотности распределения представляет собой кривую, располо-женную выше оси О х, причем эта ось является ее горизонтальной асимптотой при Замечание. Если все возможные значения непрерывной случайной величины сосредоточе-ны на интервале [ a, b ], то все интегралы вычисляются в этих пределах, а вне интервала [ a, b ] f (x) ≡ 0.
10.Числовые характеристики дискретных и непрерывных случайных величин. Математическое ожидание случайной величины и его свойства. Дисперсия случайной величины и её свойства. Закон распределения (функция распределения и ряд распределения или плотность веро-ятности) полностью описывают поведение случайной величины. Но в ряде задач доста-точно знать некоторые числовые характеристики исследуемой величины (например, ее среднее значение и возможное отклонение от него), чтобы ответить на поставленный во-прос.
|

 , что следует из определения плотности распределения.
, что следует из определения плотности распределения. Действительно,
Действительно, 
 (условие нормировки). Его справедливость следует из того, что
(условие нормировки). Его справедливость следует из того, что 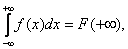 а
а 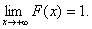
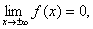 так как
так как  при
при 
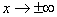 (последнее справедливо только для случайных величин, множеством возможных значений которых является все множество действительных чисел). Площадь криволинейной трапеции, ограниченной графиком этой функции, равна единице.
(последнее справедливо только для случайных величин, множеством возможных значений которых является все множество действительных чисел). Площадь криволинейной трапеции, ограниченной графиком этой функции, равна единице.


