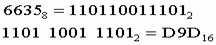Системы счисления. Двоичная, восьмеричная, шестнадцатиричная системы счисления. Примеры представления числа в указанных системах счисления
Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков. Система счисления: даёт представления множества чисел (целых или вещественных) даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление) отражает алгебраическую и арифметическую структуру чисел. Системы счисления подразделяются на позиционные, непозиционные и смешанные. Наиболее употребляемыми в настоящее время позиционными системами являются: 1 — единичная (как позиционная может и не рассматриваться; счёт на пальцах, зарубки, узелки «на память» и др.); 2 — двоичная (в дискретной математике, информатике, программировании); 3 — троичная; 4 — четверичная; 5 — пятеричная; 8 — восьмеричная; 10 — десятичная (используется повсеместно); 12 — двенадцатеричная (счёт дюжинами); 16 — шестнадцатеричная (используется в программировании, информатике, а также в шрифтах; 60 — шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты). 1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней двойки: Таблица 4. Степени числа 2
Пример. Число
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки: Таблица 5. Степени числа 8
Пример. Число
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16: Таблица 6. Степени числа 16
Пример. Число
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке. Пример. Число
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке. Пример. Число
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке. Пример. Число
7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3). Пример. Число
8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3). Пример. Число
9. Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой. Пример. Число
10. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой. Пример. Число
11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему. Пример 1. Число
Пример 2. Число
|

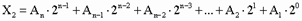
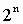
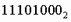 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.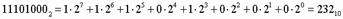
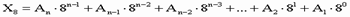
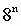
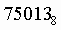 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.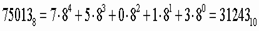
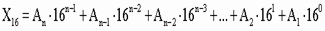
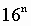
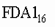 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.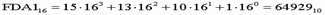
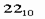 перевести в двоичную систему счисления.
перевести в двоичную систему счисления.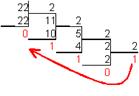

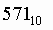 перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.
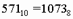
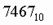 перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.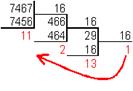
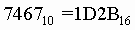
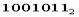 перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.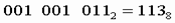
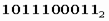 перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.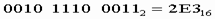
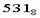 перевести в двоичную систему счисления.
перевести в двоичную систему счисления.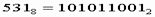
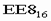 перевести в двоичную систему счисления.
перевести в двоичную систему счисления.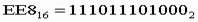
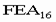 перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.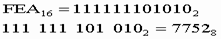
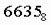 перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.