Простые механизмы.
| А 1
| С помощью простого механизма
1) можно получить выигрыш в силе, но нельзя получить выигрыш в работе
2) нельзя получить выигрыш в силе, но можно получить выигрыш в работе
3) можно получить выигрыш и в силе, и в работе
4) нельзя получить выигрыш ни в силе, ни в работе
|
КПД
| А 1
| Определите полезную мощность двигателя, если его КПД 40 %, а мощность по техническому паспорту 100 кВт.
| |
| 1) 10 кВт 2) 20 кВт
| 3) 40 кВт4) 50 кВт
| | А 2
| С помощью неподвижного блока, закрепленного на потолке, поднимают груз массой 20 кг на высоту 1,5 м. Какую работу при этом совершают, если КПД блока равен 90 %?
| |
| 1) 333 Дж2) 300 Дж
| 3) 270 Дж 4) 27 Дж
| | А 3
| С помощью системы блоков равномерно поднимают груз массой 10 кг, прикладывая силу 55 Н (см. рисунок). КПД такого механизма равен
|  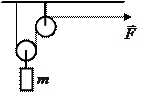
| |
| 1) 5,5 % 2) 45 %
| 3) 55 % 4) 91 %
| | А 4
| Груз перемещают равномерно по наклонной плоскости длиной 2 м. Под действием силы 2,5 Н, направленной вдоль плоскости, груз подняли на высоту 0,4 м. Если полезной считать ту часть работы, которая пошла на увеличение потенциальной энергии груза, то КПД наклонной плоскости в данном процессе равен 40 %. Какова масса груза?
| |
| 1) 50 г 2) 100 г 3) 150 г 4) 500 г
| | А 5
| Угол наклона плоскости к горизонту равен 30о. Вверх по этой плоскости тащат ящик массой 90 кг, прилагая к нему силу, направленную параллельно плоскости и равную 600 Н. Коэффициент полезного действия наклонной плоскости равен
| 
| |
| 1) 67 % 2) 75 %3) 80 % 4) 100 %
| | А 6
| Коэффициент полезного действия наклонной плоскости равен 80 %. Угол наклона плоскости к горизонту равен 30о. Чтобы тащить вверх по этой плоскости ящик массой 120 кг, к нему надо приложить силу, направленную параллельно плоскости и равную
| 
| |
| 1) 480 Н 2) 600 Н 3) 750 Н4) 1040 Н
| | | | | |
| А 7
| Плоскость, наклоненную к горизонту под углом 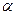 , используют для равномерного втягивания груза на некоторую высоту. Силу прикладывают вдоль плоскости. Коэффициент трения груза о плоскость равен , используют для равномерного втягивания груза на некоторую высоту. Силу прикладывают вдоль плоскости. Коэффициент трения груза о плоскость равен 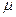 . КПД такого механизма . КПД такого механизма
| | |
| 1) невозможно рассчитать
| 2) 
| | |
| 3) 
| 4) 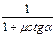
| | | А 8
| С увеличением угла наклона наклонной плоскости от 0о до 90о КПД этого простого механизма
| | |
| 1) увеличивается
2) уменьшается
3) не изменяется
4) сначала растет, затем уменьшается
| | |
| | | В 1
| С помощью рычага длиной 150 см подняли груз массой 100 кг на высоту 5 см. Какую работу совершили при этом, если КПД устройства 95 %? Ответ округлите до целых. (53 Дж)
| | | С 1
| Пушка, закреплённая на высоте 5 м, стреляет в горизонтальном направлении снарядами массой 10 кг. Вследствие отдачи её ствол, имеющий массу 1000 кг, сжимает на 1 м пружину, производящую перезарядку пушки. При этом относительная доля  энергии отдачи идет на сжатие этой пружины. Какова жесткость пружины, если дальность полёта снаряда равна 600 м? (6000 Н/м) энергии отдачи идет на сжатие этой пружины. Какова жесткость пружины, если дальность полёта снаряда равна 600 м? (6000 Н/м)
| | С 2
| Пушка, закреплённая на высоте 5 м, стреляет в горизонтальном направлении снарядами массой 10 кг. Вследствие отдачи её ствол, имеющий массу 1000 кг, сжимает пружину жесткостью 6000 Н/м, производящую перезарядку пушки. При этом относительная доля  энергии отдачи идет на сжатие этой пружины. Какова максимальная величина деформации пружины, если дальность полёта снаряда равна 600 м? (1 м) энергии отдачи идет на сжатие этой пружины. Какова максимальная величина деформации пружины, если дальность полёта снаряда равна 600 м? (1 м)
| | С 3
| Пушка, закреплённая на некоторой высоте, стреляет в горизонтальном направлении снарядами массой 10 кг. Вследствие отдачи её ствол, имеющий массу 1000 кг, сжимает на 1 м пружину жесткостью 6000 Н/м, производящую перезарядку пушки. При этом 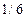 энергии отдачи идет на сжатие этой пружины. Каково время полёта снаряда, если дальность полёта снаряда равна 600 м? (1 с) энергии отдачи идет на сжатие этой пружины. Каково время полёта снаряда, если дальность полёта снаряда равна 600 м? (1 с)
| | С 4
| Пушка, закреплённая на высоте 5 м, стреляет в горизонтальном направлении снарядами массой 10 кг. Вследствие отдачи её ствол, имеющий массу 1000 кг, сжимает на 1 м пружину жесткостью 6000 Н/м, производящую перезарядку пушки. Какая доля энергии отдачи идёт на сжатие пружины, если дальность полёта снаряда равна 600 м? (1/6)
| | | | | | |

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|
Сосудистый шов (ручной Карреля, механический шов). Операции при ранениях крупных сосудов 1912 г., Каррель – впервые предложил методику сосудистого шва.
Сосудистый шов применяется для восстановления магистрального кровотока при лечении...
Трамадол (Маброн, Плазадол, Трамал, Трамалин) Групповая принадлежность
· Наркотический анальгетик со смешанным механизмом действия, агонист опиоидных рецепторов...
Мелоксикам (Мовалис) Групповая принадлежность
· Нестероидное противовоспалительное средство, преимущественно селективный обратимый ингибитор циклооксигеназы (ЦОГ-2)...
|
Решение Постоянные издержки (FC) не зависят от изменения объёма производства, существуют постоянно...
ТРАНСПОРТНАЯ ИММОБИЛИЗАЦИЯ
Под транспортной иммобилизацией понимают мероприятия, направленные на обеспечение покоя в поврежденном участке тела и близлежащих к нему суставах на период перевозки пострадавшего в лечебное учреждение...
Кишечный шов (Ламбера, Альберта, Шмидена, Матешука) Кишечный шов– это способ соединения кишечной стенки.
В основе кишечного шва лежит принцип футлярного строения кишечной стенки...
|
|