ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
© Цитович Б.В. Погрешность результата измерения (погрешность измерения) – отклонение результата измерения от истинного (действительного) значения измеряемой величины. Формально погрешность можно представить выражением D = X – Q, где D – абсолютная погрешность измерения; X – результат измерения физической величины; Q – истинное значение измеряемой физической величины. В РМГ 29 отмечается, что истинное значение величины всегда остается неизвестным, на практике вместо него используют действительное значение величины хд и погрешность измерения Δxизм определяют по формуле Δxизм = xизм – хд где xизм — измеренное значение величины. Синонимом термина «погрешность измерения» является термин ошибка измерения, применять который не рекомендуется, поскольку погрешность является неустранимым атрибутом результата измерения, а ошибка связана с нарушением процедуры измерений и должна быть устранена. Классификация погрешностей измерений может осуществляться по разным классификационным признакам (основаниям), например: · по источникам возникновения (например, инструментальные погрешности, субъективные погрешности), · по степени интегративности (интегральная погрешность и составляющие погрешности); · по характеру проявления или изменения от измерения к измерению (случайные, систематические и грубые), · по значимости (значимые, пренебрежимо малые), · по причинам, связанным с режимом измерения (статические и динамические). Рассмотрим более подробно некоторые из классификаций. Поскольку деление погрешностей по источникам их возникновения не является самоцелью, а используется для выявления составляющих, представляется достаточно логичной следующая классификация: · погрешности средств измерений(они же «аппаратурные погрешности» или «инструментальные погрешности»); · методические погрешности или «погрешности метода измерения»; · погрешности из-за отличия условий измерения от нормальных («погрешности условий»); · субъективные погрешности измерения («погрешности оператора», или же «личные» либо «личностные» погрешности). Жирным курсивом выделены термины, взятые из РМГ 29. К сожалению, этот документ включает ряд не вполне корректных терминов и определений, относящихся к источникам погрешностей измерений. Инструментальная погрешность измерения – составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений. Фактически к инструментальным погрешностям относятся погрешности всех применяемых в данных измерениях технических средств и вспомогательных устройств, влияющих на результат измерений, включая погрешности прибора, мер для его настройки, дополнительных сопротивлений, шунтов, установочных узлов или соединительных проводов и т.д. Например, при измерении массы на весах методом сравнения с мерой к погрешности весов добавляются погрешности гирь. Для измерения длины достаточно часто используют узкодиапазонные приборы, которые настраивают по концевым мерам длины. Так при измерении диаметра d детали индикатором часового типа на стойке (рисунок 5.1), инструментальные погрешности складываются из погрешностей самой измерительной головки 1, погрешностей стойки 2 и погрешностей блока плоскопараллельных концевых мер длины 3, на который настраивался прибор.
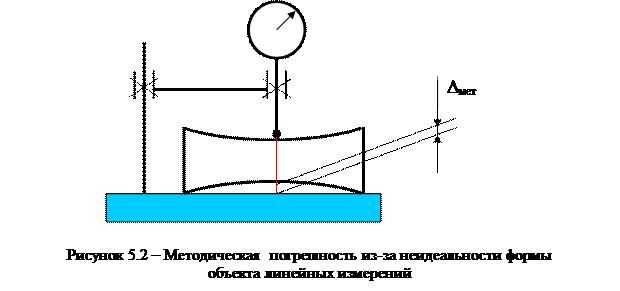
В свою очередь каждую из приведенных инструментальных составляющих погрешности измерения можно разбить на элементарные составляющие. Например, погрешность измерительной головки 1 включает в себя множество составляющих, которые зависят от ее конструкции. Погрешности элементов стойки 2 (колонка, кронштейн, рабочая поверхность стола) приводят к неправильному ориентированию прибора и детали. Погрешности блока плоскопараллельных концевых мер длины 3, на который настраивался прибор, определяются погрешностями каждой из мер блока и погрешностями их притирки. Погрешность метода измерений (погрешность метода) – составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений. В примечаниях говорится, что иногда погрешность метода может проявляться как случайная. Если погрешность от некоторого источника может проявляться как систематическая и как случайная, не имеет смысла связывать характер погрешности с ее источником. Чтобы не связывать «метод измерений» и «погрешность метода», поскольку прямой связи здесь нет, предпочтительно рассматриваемый класс погрешностей называть «методическими погрешностями». Методические погрешности могут возникать из-за несоответствий реальной методики выполнения измерений идеальным теоретическим положениям, на которых основаны измерения. Эти погрешности делятся на две группы. К первой можно отнести погрешности из-за допущений, принятых при измерении или обработке результатов, а также используемых в ходе измерительного преобразования приближений и упрощений (погрешности из-за несоответствия процесса измерительного преобразования его идеальной модели). Другой возможной причиной погрешностей метода является некорректная идеализация реального объекта измерений (несоответствие объекта измерения модели, положенной в основу процесса измерения). Рассмотрим примеры погрешностей первой группы. При косвенных измерениях диаметров больших деталей часто рулеткой измеряют длину окружности, а затем рассчитывают диаметр. Здесь в любом случае будет присутствовать погрешность из-за округления трансцендентного числа p. По той же причине образуются методические погрешности при измерении площади круглых сечений, объема тел с такими сечениями и плотности их материала. При измерении азимута по магнитному компасу методическая погрешность возникает из-за несовпадения магнитных и географических полюсов Земли. Измерение параметров электрической цепи специально подключаемым прибором приводит к изменению структуры цепи из-за подключения дополнительной нагрузки. Результаты измерений электрических параметров объектов также могут искажаться из-за наличия присоединительных проводов, меняющихся переходных сопротивлений в местах присоединения чувствительных элементов (щупов или клемм) измерительных приборов. Измерение массы взвешиванием на весах с гирями в воздушной среде осуществляют, как правило, без учета воздействия на меры и объект выталкивающей архимедовой силы, которой бы не было при взвешивании в вакууме. В большинстве случаев погрешности из-за принятых допущений пренебрежимо малы, но в случае прецизионных измерений их приходится оценивать и учитывать или компенсировать. Появление методической погрешности второй группы (погрешности из-за некорректной идеализации реального объекта измерений) можно рассмотреть на примере измерения диаметра номинально цилиндрической детали станковым средством измерений (измерительной головкой на стойке). В частности, измерение детали с седлообразной поверхностью приведет к появлению методической погрешности, примерно равной отклонению образующей от прямолинейности (рисунок 5.2).
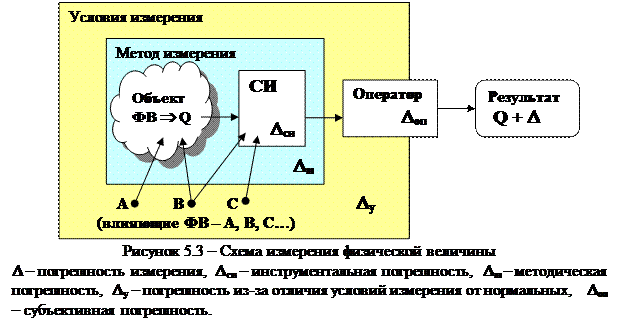
Анализ приведенного примера показывает, что некорректная идеализация формы объекта при линейных измерениях может привести к возникновению методических погрешностей, которые могут существенно превышать инструментальную составляющую. При измерении плотности номинально компактного и однородного твердого тела неидеальность объекта может быть связана с наличием необнаруженных полостей или инородных включений. Перечень видов неидеальности объектов может быть значительно расширен. Например, значения параметров твердости и шероховатости поверхностей деталей, химический состав материала детали, определяемые на конкретном участке, могут отличаться от параметров на других участках той же поверхности. Температура в объеме жидкости или газа практически всегда различается по слоям (температурные градиенты), скорость жидкости или газа в потоке в разных сечениях неодинакова (градиенты скорости) и т.д. Погрешность (измерения) из-за изменений условий измерения – составляющая систематической погрешности измерения, являющаяся следствием неучтенного влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения. Примечание — Этот термин применяют в случае неучтенного или недостаточно учтенного действия той или иной влияющей величины (температуры, атмосферного давления, влажности воздуха, напряженности магнитного поля, вибрации и др.); и др. Как и в предыдущем случае, определение содержит неправомочное указание на систематический характер погрешности. Погрешность связывают с отклонением влияющей величины в одну сторону (а как быть с ее колебанием при многократных измерениях?). «Неучтенное или недостаточно учтенное влияние» не имеет никакого смысла в определении источника погрешности – это проблема обнаружения и оценки погрешности. Наиболее логичным представляется термин «погрешности из-за отличия условий измерения от идеальных (от нормальных)». Обычно такие погрешности называют «погрешностями условий», что не совсем корректно, но подразумевает то же содержание. Фактически эти погрешности имеют место тогда, когда не удается выдержать нормальные условия измерений. Нормальные условия связаны с понятием влияющих физических величин. Влияющая физическая величина – физическая величина, оказывающая влияние на размер измеряемой величины и (или) результат измерений. Определение требует расшифровки: фактически под влияющими физическими величинами понимают те, которые не являются измеряемыми, но влияют на результаты измерений, воздействуя на объект и/или средства измерений Пределы допустимых изменений таких величин или их отклонений от номинальных значений нормируют либо нормальной областью значений (нормальные условия измерений) или рабочей областью значений (рабочие условия измерений). Поскольку при нормальных условиях измерений влияющие величины отличаются от номинальных значений, погрешности обязательно возникают. Однако нормальные условия назначают таким образом, чтобы «погрешности условий» оказались пренебрежимо малыми, например, по сравнению с инструментальными составляющими. В таком случае «погрешности условий» можно считать практически равными нулю. К погрешностям из-за несоблюдения нормальных условий измерений следует отнести все составляющие погрешности измерения, которые вызваны воздействием на измеряемый объект и средства измерений любойвлияющей физической величины, выходящей за пределы нормальной области значений. Влияющие величины обычно обусловлены температурными, электромагнитными и другими полями в рабочей зоне (измерительная позиция и ближайшее окружение), давлением воздуха, его избыточной влажностью, наличием вибраций на рабочем месте, где выполняются измерения. Есть множество факторов, которые могут привести к искажению самой измеряемой величины и (или) измерительной информации о ней. Например, изменение температуры тела не приводит к изменению его массы, но вызывает изменения линейных размеров, сопротивления прохождению электрического тока. Повышенная влажность не влияет на размеры металлических деталей, но может привести к изменению размеров и массы изделий из гидрофильных материалов, которые впитывают влагу из окружающей атмосферы. Поиск влияющих величин осуществляется при анализе конкретной методики выполнения измерений. В процессе проведения анализа следует внимательно относиться к «дополнительным погрешностям средств измерений», возникающим из-за действия влияющих величин, поскольку учет только этих составляющих может привести к «потере» результатов воздействия тех же влияющих величин на объект измерения. «Погрешности условий» могут возникать либо из-за закономерно изменяющегося отличия влияющей величины от ее номинального значения, либо из-за стохастических колебаний около него. Например, если рассматривать температурные погрешности, то они могут возникать из-за стабильного отличия температуры от нормальной (при измерениях длины температура детали 25 о С, а не 20 о С вызовет постоянную температурную погрешность), а постепенный рост температуры в помещении от начала к концу рабочей смены приведет к переменной температурной погрешности. Как бы мы ни старались поддерживать постоянную температуру в помещении, никакие технические устройства не обеспечат ее абсолютной стабильности. Невозможно полностью компенсировать воздействия ряда случайных факторов (изменение теплового баланса при движении воздушных масс в помещении, при воздействии солнечных лучей, при вносе и выносе деталей, перемещении операторов, включении и выключении приборов и т.д.). В результате возникают стохастические колебания температуры и случайно изменяющаяся составляющая температурной погрешности. Субъективная погрешность измерения – составляющая систематической погрешности измерений, обусловленная индивидуальными особенностями оператора. Иногда субъективную погрешность называют личной погрешностью или личной разностью. Понятно, что определять характер этой погрешности как систематический нет никаких оснований Субъективные погрешности включают погрешности отсчитывания и погрешности манипулирования средствами измерений и измеряемым объектом. Погрешности отсчитывания возникают при использовании аналоговых средств измерений с устройством выдачи измерительной информации типа «шкала-указатель». При положении указателя между отметками шкалы отсчитывание осуществляется либо с округлением до ближайшего деления, либо с интерполированием доли деления на глаз. Погрешность округления результата до целого деления составляет не более половины цены деления отсчетного устройства, а при интерполировании опытным оператором и удачной эргономике отсчетного устройства погрешность отсчитывания еще меньше и составляет не более 1/10 части цены интерполируемого деления. В случае, если плоскости шкалы и указателя не совпадают, возможно возникновение погрешности отсчитывания из-за параллакса при «косом» направлении взгляда оператора. Для уменьшения погрешностей от параллакса используют методы сближения указателя со шкалой (скошенные кромки нониуса штангенциркуля и барабана микрометра, расположенный в плоскости шкалы световой указатель) или искусственные приемы получения нормального угла зрения (специальные наглазники и налобники в оптических приборах, зеркальная полоска под шкалой прецизионных приборов и др.). Очевидно, что погрешности отсчитывания при округлении или интерполировании и погрешности из-за параллакса не возникают при использовании приборов с дискретной выдачей информации на цифровых табло. При измерениях часто приходится оперировать устройствами совмещения, настройки и корректировки нуля, арретирования, базирования средства измерений или измеряемого объекта, чувствительными элементами средства измерений. Эти манипуляции часто приводят к погрешностям, особенно существенным у операторов с недостаточно высокой квалификацией. Принятое в некоторых источниках деление субъективных погрешностей на «погрешности присутствия», «погрешности отсчитывания», «погрешности действия» и «профессиональные погрешности» неудачно. Поскольку под «погрешностями присутствия» понимают те, которые вызваны температурными (и другими) полями оператора, представляется более правильным рассматривать оператора как один из источников возмущения, вызывающий искажение условий измерения. К «погрешностям действия» почему-то не относят погрешности отсчитывания. «Профессиональные погрешности» связывают с квалификацией оператора. Очевидно, что не стоит выделять эти погрешности в отдельную группу: высокая квалификация оператора позволяет свести к минимуму как погрешности манипулирования средствами и объектами измерений, так и погрешности отсчитывания. Особенностью высококвалифицированных операторов является преобладание в личностных погрешностях систематической составляющей, в то время как у операторов с малым опытом доминируют случайные погрешности. Аналогичное явление наблюдается при рассеянии результатов попадания в мишень у опытных и начинающих стрелков. Распределение источников погрешностей можно проиллюстрировать на схеме измерения физической величины (рисунок 5.3).
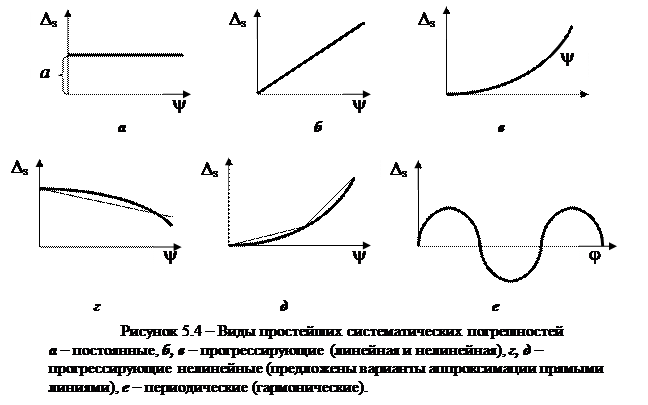
В данной схеме взаимодействие средства измерений с измеряемым объектом определяет «метод измерения», следовательно, и методические погрешности. «Условия измерений» на схеме взяты в широком смысле и включают в себя не только влияющие величины, но и факторы, оказывающие отрицательное воздействие на оператора (недостаточная освещенность, шумовое загрязнение среды и др.). Тем не менее, оценивать «погрешность условий» предлагается только как результат действия влияющих величин (величины типа А воздействуют только на измеряемый объект, типа В – на измеряемый объект и на средство измерений, типа С – только на средство измерений). В метрологической литературе встречаются и другие классификации погрешностей измерений по источникам возникновения. Абсолютно строгой классификации источников погрешностей быть не может, поскольку воздействия источников переплетаются. Так методические погрешности в некоторой степени определяются выбранным средством измерений, условия измерений (если они связаны с теми влияющими величинами, которые оказывают воздействие на средства измерений) можно рассматривать как источник дополнительных инструментальных погрешностей, дискомфортные условия измерений приводят к увеличению субъективных погрешностей и т.д. Следует помнить, что классификации погрешностей в метрологии имеют четко определенное целевое назначение – использование при анализе методик выполнения измерений для выявления погрешностей и оценки их значений. Главное – не упустить значимые погрешности, воспользовавшись любой подходящей классификацией источников погрешностей измерений. Представленная на рисунке 5.3 схема, как показывает практика, соответствует поставленной цели поиска составляющих погрешностей измерений. Погрешность измерения D, которая всегда является интегральной погрешностью, образуется в результате объединения составляющих погрешностей от разных источников: D = Dси* Dм *Dу *Dоп , где * – знак объединения (комплексирования а не алгебраического сложения), поскольку погрешности разного характера объединяют с использованием разных математических операций. Каждый из источников может дать одну, либо несколько элементарных составляющих. В последнем случае составляющая погрешность сама является интегральной. В качестве примеров, иллюстрирующих множество составляющих в одном источнике, можно представить представленные выше результаты рассмотрения субъективной и инструментальной погрешностей. В метрологической литературе встречаются разные классификации погрешностей измерений по характеру их проявления (изменения). Традиционным является деление погрешностей на случайные, систематические и грубые, и этот же подход принят в стандартах. Однозначно распределить погрешности в соответствии с принятым в стандарте делением на систематические и случайные в ряде случаев не удается из-за возможности произвольной трактовки их определений. Результаты нечеткого деления погрешностей приводят к явно нелепым ситуациям. Например, в некоторых источниках, включая РМГ 29 – 99, погрешности методические, «условий» и субъективные относят к систематическим. Такая позиция способствует образованиюнеправильного стереотипа, увязывающего характер погрешности с источником ее появления. Очевидно, что одни и те же погрешности в некоторых случаях могут проявляться либо как систематические, либо как случайные. В литературе встречается подход, который трактует распределение погрешностей на систематические и случайные как один из приемов анализа. Принятие этой концепции равноценно признанию возможности приписывания погрешностям произвольно выбранного характера проявления. Реальное положение характеризуется фактическим наличием как детерминированных, так и случайных (стохастических) явлений, которые вызывают появлениесоответствующих погрешностей. Например, наряду с закономерным изменением длины стержня при повышении или понижении температуры широко известно броуновское движение, которое следует рассматривать как проявление стохастических (случайных) явлений, проходящих на молекулярном уровне. Надо признать также возможность объединенного воздействия множества явлений, которые по отдельности имеют функциональную природу, но в итоге комплексирования при измерениях приводят к появлению случайных результатов из-за неопределенности действующих факторов, малости воздействия каждого из них и неоднозначности объединения воздействий отдельных факторов. При большом числе действующих факторов такой механизм приводит к стохастическому характеру комплексных воздействий. Подобные механизмы действуют при бросании игральных костей, игре в рулетку, выбрасывании «лототроном» шара с определенным номером. Описанные системы используют как генераторы случайных чисел. Поскольку механизмы образования значительной части составляющих погрешности измерений сходны с механизмами формирования случайных величин, можно ожидать наличия в результатах измерений случайных погрешностей. Если это допущение справедливо, то после исключения систематических погрешностей для обработки результатов измерений можно использовать аппарат теории вероятностей и математической статистики. С другой стороны, очевидно наличие детерминированных механизмов образования погрешностей. И средства измерений, и измеряемые объекты, и окружающая среда подчиняются физическим законам. Поэтому при взвешивании груза на пружинных весах надо считаться с широтой и высотой над уровнем моря, при измерении длины следует учитывать температурные изменения объема тел, при использовании емкостных преобразователей приходится рассматривать диэлектрические свойства воздуха, а его оптические свойства – при измерении длины лазерным интерферометром. Анализ стандартных определений погрешностей измерения позволяет выявить их недостатки и откорректировать содержание широко применяемых терминов. По РМГ 29 – 99 систематическая погрешность измерения (систематическая погрешность) – составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Упоминание повторных измерений одной величины некорректно, так как систематика погрешностей может проявляться и при измерениях физических величин разных размеров. В частности, неправильная настройка прибора на ноль («сбитый ноль») приводит к появлению постоянной составляющей погрешности при любых измерениях, проводимых до изменения настройки. К систематическим погрешностям измерений можно отнести те составляющие, для которых можно считать доказанным наличие функциональных связей с вызывающими их аргументами. Для них можно предложить формальную запись в виде D s = F (j, y...), где j, y – аргументы, вызывающие систематическую погрешность. Главной особенностью систематической погрешности является принципиальная возможность ее выявления, прогнозирования и однозначной оценки,если удается узнать вид функции и значения аргументов. В зависимости от характера измерения систематические погрешности подразделяют на элементарные и изменяющиеся по сложному закону. Элементарные погрешности можно условно разделить на постоянные, прогрессирующие (прогрессивные) и периодические. Прогрессирующими называют монотонно возрастающие или монотонно убывающие погрешности. Периодические погрешности – погрешности, изменение которых можно описать периодической функцией. Погрешности, изменяющиеся по сложному закону, образуются при объединении нескольких систематических погрешностей. Разновидности систематических погрешностей представлены в графической форме на рисунке 5.4.
Графики постоянных систематических погрешностей представлены на рисунке 5.4 а (D s = a, или D s = const), а переменных – на рисунках 5.4 б – е. Простейшие переменные систематические погрешности, которые аппроксимируют графиками без перегибов (это монотонно изменяющиеся или прогрессирующие погрешности) показаны на рисунках 5.4 б – г, а периодические или гармонические погрешности – на рисунке 5.4 е. Всем известны «спешащие» и «отстающие» часы, погрешности которых прогрессируют во времени, но мало кто анализирует показания часов за полный оборот стрелки. Если оценивать погрешности, то можно утверждать, что в результате многократного повторения вращения стрелки часов должны проявляться периодические погрешности, обусловленные эксцентриситетом и превращающиеся в нуль при завершении каждого полного оборота. Обычно для описания и для аппроксимации систематической погрешности подбирают наиболее простую функцию, например линейную для прогрессирующей погрешности. Такой же упрощенный подход применяют и для аппроксимации гармонической систематической погрешности, которая может быть описана как синусоида, косинусоида, пилообразная либо другая периодическая функция. Систематическая погрешность может иметь не только элементарный, но и более сложный характер, который можно аппроксимировать функцией, включающей приведенные простые составляющие. Сложная систематическая погрешность, включающая постоянную, прогрессирующую и периодическую составляющие, в общем виде может быть описана выражением D s = a + by + dsinj, где a – постоянная составляющая сложной систематической погрешности; y, j – соответственно аргументы прогрессирующей и периодической составляющих сложной систематической погрешности. Альтернативой систематической погрешности является случайная погрешность. Стандартное определение случайной погрешности измерения в строгом смысле не является определением, поскольку содержит «порочный круг»: составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины. Здесь также использовано некорректное упоминание измерений одной и той же величины, а, кроме того, содержится бессмысленная характеристика качества выполнения измерений («проведенных с одинаковой тщательностью»). Случайными погрешностями в строгом смысле термина можно считать только те, которые обладают статистической устойчивостью (ведут себя как центрированная случайная величина). Причиной появления таких погрешностей чаще всего является совокупное действие ряда слабо влияющих дестабилизирующих факторов, связанных с любыми источниками погрешностей, причем функциональные связи аргументов с погрешностями либо отсутствуют (в наличии только стохастические зависимости), либо не могут быть выявлены из-за неопределенности факторов и большого их числа. Погрешности, которые ведут себя как центрированные случайные величины, можно оценивать вероятностно, применяя для этого математический аппарат теории вероятностей и математической статистики. Каждую из таких погрешностей нельзя предсказать индивидуально, но можно оценить вероятность их появления в определенном интервале значений. Погрешности, которые нельзя отнести ни к случайным, ни к систематическим из-за совершенно иного механизма образования и значения, принципиально отличного от ожидаемого, называют грубыми погрешностями измерений или промахами. Промах – погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Определение промаха сформулировано весьма неудачно, в первую очередь некорректным является упоминание «данных условий». Очевидно, что причинами возникновения грубой погрешности могут быть промах оператора при снятии отсчета или его записи, ошибка в реализации методики измерений, сбой в измерительной цепи прибора или незамеченное импульсное изменение влияющей физической величины. Причины появления результатов с грубыми погрешностями резко выпадают из ряда механизмов, формирующих систематические или случайные составляющие погрешности измерений. Однако «резкое отличие» не является критерием и оставляет значительные возможности для произвола. «Результат измерения с грубой погрешностью» фактически вызван ошибкой, допущенной при измерении, поэтому результаты с грубыми погрешностями следует признать ошибочными и подлежащими устранению. В некоторых метрологических источниках грубые погрешности измерений относят к случайным, что соответствует вульгарной трактовке понятия случайности и маскирует различия механизмов возникновения собственно случайных и грубых погрешностей. Грубые погрешности в принципе непредсказуемы, а их значения невозможно прогнозировать с учетом вероятности как это делают для случайных погрешностей. Фактически к результатам с грубыми погрешностями относят либо такие, которые явно не соответствуют ожидаемому результату измерений (нелепые результаты), либо экстремальные значения, отличия которых от средних значений массива выражены не столь откровенно, но принадлежность которых к данному массиву результатов имеет весьма малую вероятность. Отбрасывание (элиминация) результатов с грубыми погрешностями предупреждает возможность значительного искажения оценки результатов измерений. Исключение результатов может осуществляться либо цензурированием явно нелепых значений, либо статистическим отбраковыванием экстремальных результатов (подозрительных на наличие грубых погрешностей), которое основано на принципе практической уверенности. Применение этого принципа позволяет отбрасывать те значения, вероятность появления которых в исследуемом массиве данных меньше некоторой заранее выбранной. По значимости все погрешности (составляющие и интегральные) можно делить на значимые и пренебрежимо малые. К пренебрежимо малым составляющим относят погрешности, которые значительно меньше доминирующих составляющих. Соотношение между пренебрежимо малой D min и доминирующей Dmax составляющими можно записать в виде
|