Разложение функций в степенные ряды.
1. Определение 1. Формула Тейлора. 2. Определение 2. Ряд Тейлора и ряд Маклорена. 3. Теорема 1. Необходимое и достаточное условие разложимости функции в ряд Тейлора. 4. Приемы разложения в степенной ряд. 5. Таблица разложений в степенной ряд (ряд Маклорена) 6. Пример 1. Разложить в степенной ряд по степеням 7. Пример 2. Разложить в степенной ряд по степеням 8. Пример 3. Разложить в степенной ряд по степеням 9. Пример 4. Используя разложение в ряд функции 10. Пример 5. Разложить функцию 11. Приближенное вычисление значений функций. 12. Пример 6. Вычислить приближенное значение 13. Пример 7. Вычислить приближенное значение корня 14. Применение степенных рядов в приближенных вычислениях определенных интегралов. 15. Пример 8. Вычислить: 16. Применение степенных рядов в приближенном интегрировании обыкновенных дифференциальных уравнений. 17. Пример 9. Найти решение дифференциального уравнения 18. Применение степенных рядов к вычислению пределов. 19. Пример 10. Вычислить
|
функцию 
.
.
.
.
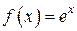в ряд по степеням х.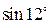
с точностью до 0,001.
с точностью до 0,001.
. Вычислить 
с точностью до 0,01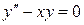
, удовлетворяющее начальным условиям 
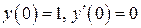(задача Коши).
.
