Символы, рекомендованных к использованию в данной работе
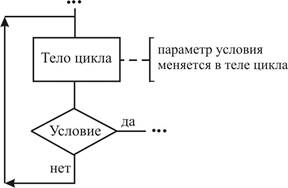
Циклический алгоритм может представлен в виде следующих основных структур: - цикл - ДО; - цикл - ПОКА; - цикл с параметром. Цикл - ДО начинается с выполнения тела цикла, затем проверяется условие окончания цикла, таким образом тело цикла обязательно будет реализовано хотя бы один раз. Такую разновидность цикла еще называют циклом с постусловием. В стандартном виде цикл выполняется до тех пор пока условие не станет истинным. Словесная запись соответствующего цикла может быть определена как: повторять тело цикла до выполнения заданного условия. Графически данная конструкция может быть представлена: а) с использованием блока решение; б) с использованием блоков начало и конец цикла а) Цикл - ДО с блоком решения (устаревшая конструкция алгоритма)
б) Цикл - ДО с блоками начало и конец цикла
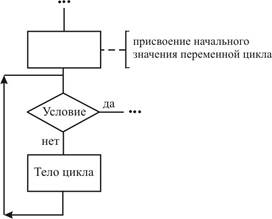
Цикл - ПОКА начинается с проверки условие окончания цикла, поэтому такую разновидность цикла называют еще циклом с предусловием. Стандартно цикл выполняется только в том случае, когда условие истинно. В частности, может оказать, что тело цикла не будет выполнено ни разу если с самого начала условие продолжения цикла не выполнялось. Словесная запись соответствующего цикла может быть определена как: пока выполняется заданное условие выполнять тело цикла. Графически данная конструкция может быть представлена: а) с использованием блока решение; б) с использованием блоков начало и конец цикла. а) Цикл - ПОКА с блоком решение
б) Цикл - ПОКА с блоками начало и конец цикла
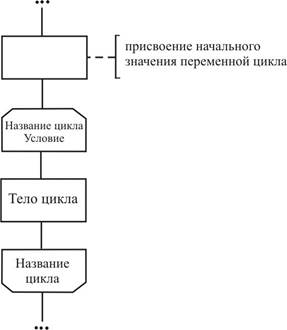
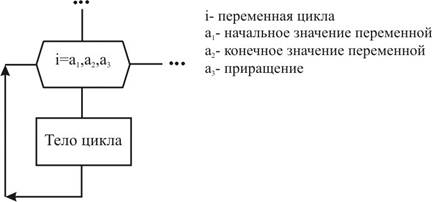
Для того чтобы не происходило "зацикливание" (бесконечное повторение тела цикла), необходимо, чтобы в теле цикла осуществлялись преобразования, приводящие к изменению параметра входящего в условие завершения цикла. Цикл с параметром представляет собой такую управляющую структуру, которая используется в тех случаях, когда тело цикла выполняется при каждом значении некоторого параметра, изменяющегося в заданных пределах с заданным шагом, т.е. количество циклов заранее известно. Словесная запись такой структуры может выглядеть так: для каждого параметра i, изменяющегося от A до B с шагом C, выполнять тело цикла. Графически данная конструкция может быть представлена с использованием символа подготовка:
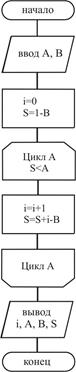
Рассмотренный цикл параметром еще называют арифметическим циклом, если шаг изменения параметра равен единице, то его можно не указывать. Примеры построения алгоритмов: Задача 1. Вычислить сумму n первых десяти членов прогрессии прогрессии.
Задача 2. Определить количество первых членов прогрессии
2. Описание практической части работы: 2.1. Цели лабораторной работы: Изучить построение циклических алгоритмов, решить задачу с помощью организации арифметических и логических циклов. 2.2. Постановка задачи: В соответствии с номером варианта найти значение функции, заданной одним или несколькими математическими выражениями. 2.3. Порядок выполнения работы: 2.3.1. Ознакомиться с теоретической частью. 2.3.2. Получить задание у преподавателя. 2.3.3. Выполнить работу. 2.3.4. Оформить отчет: 2.3.4.1. Содержание отчета: 1. Цель работы - краткая формулировка поставленной цели. 2. Порядок выполнения - определяются действия, необходимые для выполнения данной работы. 3. Постановка задачи - формулирование задачи в соответствии с индивидуальным заданием. 4. Решение поставленной задачи: 4.1. Математическое описание решения поставленной задачи содержит описание связей между параметрами с использованием принятых в математике обозначений. 4.2. Описание логической структуры программы (алгоритм решения) содержит: - краткое описание схемы программы, - алгоритм решения (по ГОСТ) - рисунок, - краткое описание используемых операторов языка программирования (при необходимости). 4.3. Описание программы содержит: · название файла, его размер, · текст программы (или фрагмент для решения конкретной, наиболее важной части задания). 4.4. Результат работы программы: - значения, полученные в результате выполнения программы - анализ полученных результатов. Выводы – отвечают на поставленную цель.
2.4. Контрольные вопросы: 1. Дайте определение алгоритма? 2. Назовите свойства алгоритмов? 3. Каким образом можно описать алгоритм решения задачи? 4. Чем характеризуется циклическая структура алгоритма? 5. Каким образом отображается циклическая структура алгоритма на блок-схеме? 6. Чем отличается цикл ДО от цикла ПОКА? 7. Как изображается в схеме программы логический цикл? 8. Какой из циклов эффективнее (быстрее выполняется в программе) логический или арифметический? 9. Когда предпочтительнее использовать арифметический цикл в программе, написанной на языке Basic Microsoft? 10. Что такое пустой цикл и зачем он бывает нужен в программе? Таблица
|


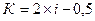 , где K и i соответственно значение и номер члена
, где K и i соответственно значение и номер члена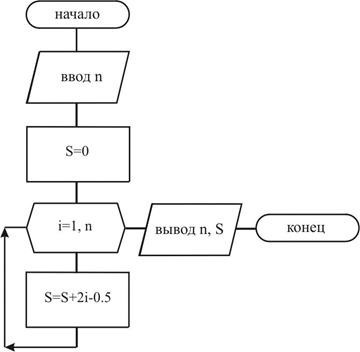
 , сумма которых не превышает заданное число A, где K и i соответственно значение и номер члена прогрессии.
, сумма которых не превышает заданное число A, где K и i соответственно значение и номер члена прогрессии.