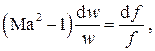Закон обращения геометрического воздействия
Для более детального выяснения механизма перехода потока через скорость звука рассмотрим совместно уравнения I начала термодинамики для потока, уравнение неразрывности и уравнение адиабатического процесса течения, которое в данном случае удобнее представить в дифференциальной форме при принятых выше допущениях. Имеем
Из первого и третьего уравнений находим
Подставив это отношение в уравнение неразрывности и учтя, что
Отношение скорости потока в данном сечении канала к местной скорости звука называется числом Маха,
С учетом этого определения получаем выражение
известное под названием закона обращения геометрического воздействия. Закон обращения геометрического воздействия позволяет выяснить общую конфигурацию сопел, обеспечивающую полное расширение газа до давления среды за соплом, и, как следствие этого, получить максимально возможную скорость на выходе. Отметим прежде всего, что площадь поперечного сечения сопла f и скорость потока w положительны, дифференциал d w положителен для сопел по определению. Тогда из закона обращения геометрического воздействия следует, что знак d f т.е. расширение или сужение поперечного сечения сопла, будет определяться соотношением между скоростью потока и местной скоростью звука. Рассмотрим три случая. 1. Скорость потока на входе меньше местной скорости звука, т.е. w<a, Ma<1, Ma2–1<0, откуда следует d f < 0, т.е. для ускорения дозвукового потока сопло должно быть суживающимся. 2. Скорость потока на входе равна местной скорости звука, т.е. w=a, Ma=1, Ma2–1=0, откуда следует d f = 0, т.е. скорость потока становится равной местной скорости звука. Таким образом, скорость потока становится равной местной скорости звука в минимальном сечении сопла. 3. Скорость потока на входе больше местной скорости звука, т.е. w>a. Тогда Ma>1, Ma2–1>0, откуда следует d f > 0, т.е. для ускорения сверхзвукового потока сопло должно быть расширяющимся. Все эти случаи показаны на рис.7.3.
Сопло, позволяющее ускорить дозвуковой поток до сверхзвуковых скоростей, должно, таким образом, состоять из двух участков – суживающегося, где ускорение происходит до местной скорости звука, и расширяющегося насадка, где поток приобретает сверхзвуковую скорость. Такое комбинированное сопло было предложено французским инженером П.Лавалем и носит его имя. Конфигурация сопла Лаваля приведена на рис.7.4.
|

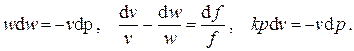
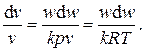
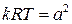 , где a – скорость звука, получаем
, где a – скорость звука, получаем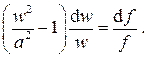
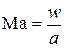 .
.