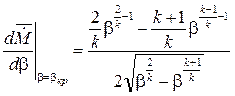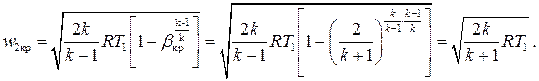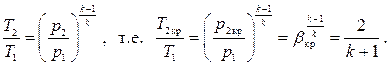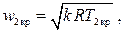Скорость истечения и расход в адиабатически изолированных каналах без трения
Первый закон термодинамики легко интегрируется, так как входящие в него дифференциалы являются полными:
причем этот результат справедлив как для обратимого течения, так и для необратимого. Обычно определяют скорость w2 потока в выходном сечении канала:
Обычно скорость на выходе сопла w2 значительно превышает скорость на входе w1, тогда
Разность энтальпий при течении в адиабатических соплах равна полезной внешней работе потока, откуда
В случае идеального газа на основании выражения для полезной внешней работы адиабатического процесса получаем
Массовый расход газа при известной скорости в выходном сечении находится на основании определения
где удельный объем в выходном сечении находится из условия адиабатичности процесса, т.е.
С учетом этого выражение для массового расхода идеального газа принимает вид
Построим графики зависимости скорости истечения газа из сопла w 2 и массового расхода газа
причем β может изменяться в пределах от 0 до 1, так как давление газа p2 на выходе для сопел по определению меньше давления на входе p1 и оба они положительны. Для упрощения графического представления введем также безразмерные скорость истечения и массовый расход с помощью равенств
Тогда для безразмерных скорости истечения и расхода получаем следующие выражения:
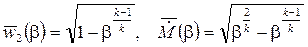 . .
Графики этих функций показаны на рис.7.2. Формулы для скорости и расхода справедливы в интервале значений отношения давлений β от некоторого критического βкр до единицы, причем при
Приравнивая числитель нулю при β= βкр, получаем
Таким образом, критическое отношение давлений при адиабатном течении идеального газа в соплах зависит только от его показателя адиабаты, т.е. от числа атомов в молекулах газа. Значения βкр представим в таблице. Здесь же приведено ориентировочное значение критического отношения давлений для водяного пара вблизи верхней пограничной кривой, которое может быть использовано для практических расчетов. Таблица 3 Критическое отношение давлений
Критическому отношению давлений βкр в соответствует скорость истечения из адиабатического сопла:
Для адиабатного процесса
Тогда скорость истечения газа при βкр равна
а это не что иное, как скорость звука в газах, т.е. скорость распространения малых возмущений давления, плотности и т.д. Таким образом, аномалия в поведении скорости потока в адиабатическом сопле связана с переходом от дозвукового режима течения к сверхзвуковому.
Лекция 15
|

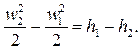
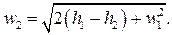
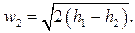
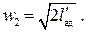
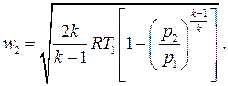
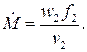
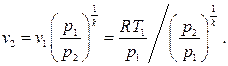
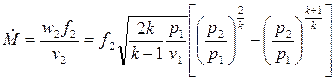 .
.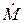 от отношения давлений за соплом p 2 и перед соплом p 1, для чего введем обозначение
от отношения давлений за соплом p 2 и перед соплом p 1, для чего введем обозначение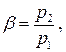
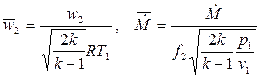 .
.
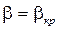 массовый расход принимает максимальное значение. В интервале же
массовый расход принимает максимальное значение. В интервале же 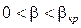 массовый расход не зависит от отношения давлений β и оказывается равным
массовый расход не зависит от отношения давлений β и оказывается равным 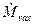 , в то время как теория дает ниспадающую до нуля ветвь. Скорость потока в этом же интервале β может вести себя двояким образом: либо возрастать с уменьшением отношения давлений, либо оставаться постоянной и равной скорости при критическом отношении давлений βкр. Вычислим βкр из условия максимума массового расхода:
, в то время как теория дает ниспадающую до нуля ветвь. Скорость потока в этом же интервале β может вести себя двояким образом: либо возрастать с уменьшением отношения давлений, либо оставаться постоянной и равной скорости при критическом отношении давлений βкр. Вычислим βкр из условия максимума массового расхода: