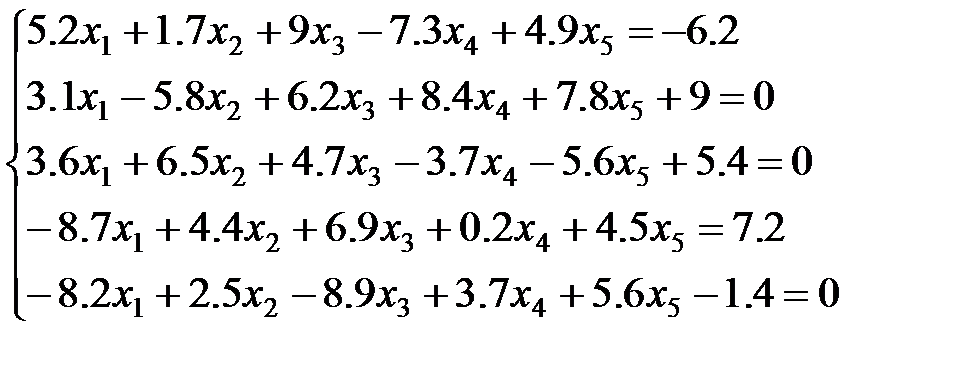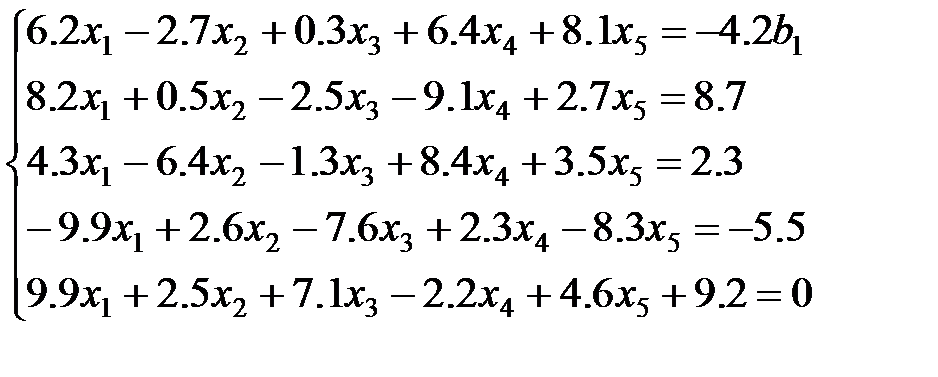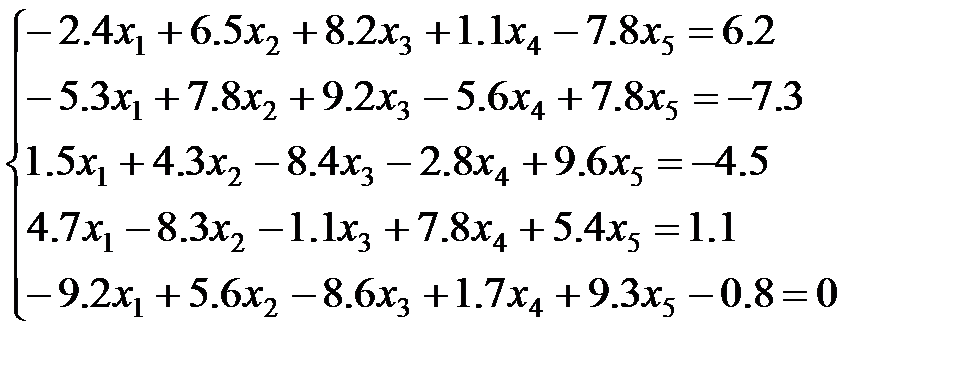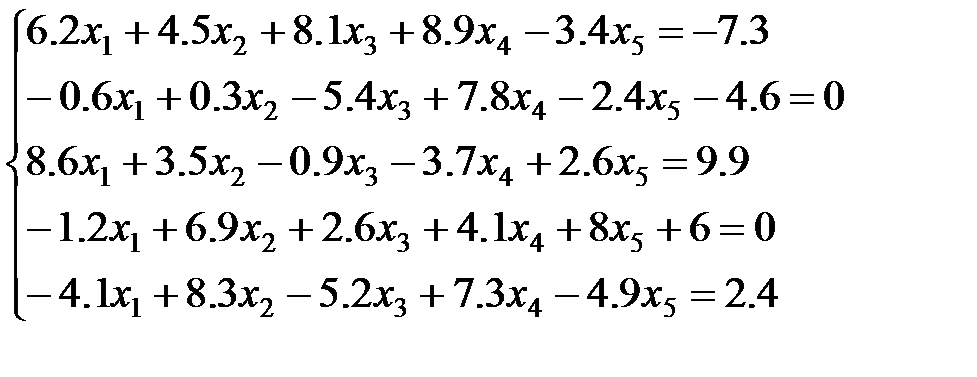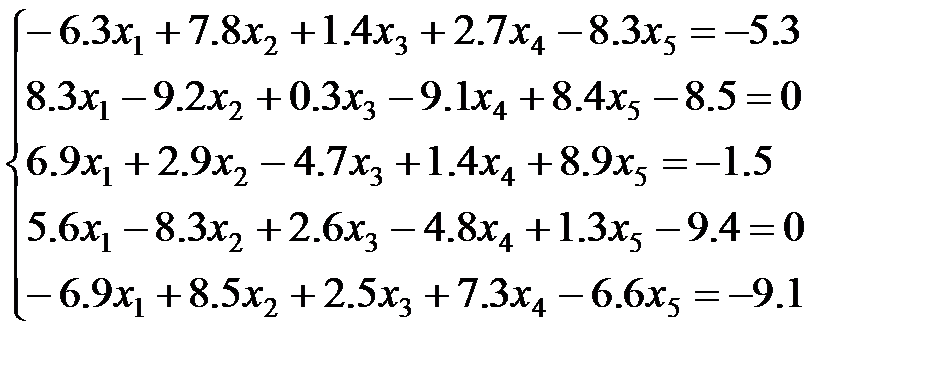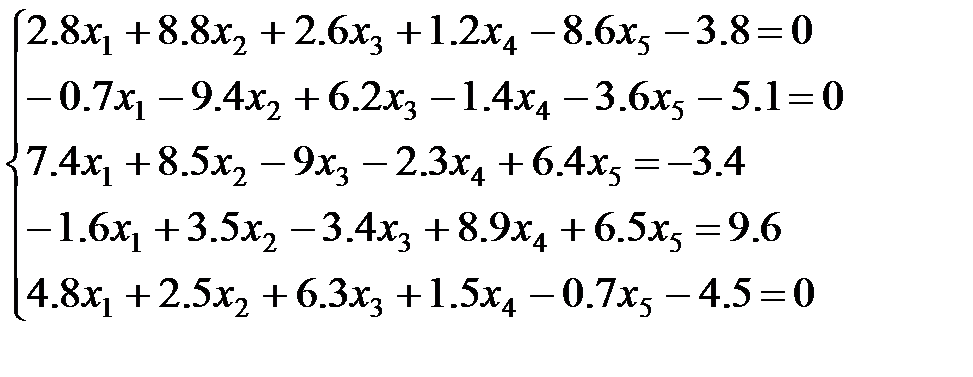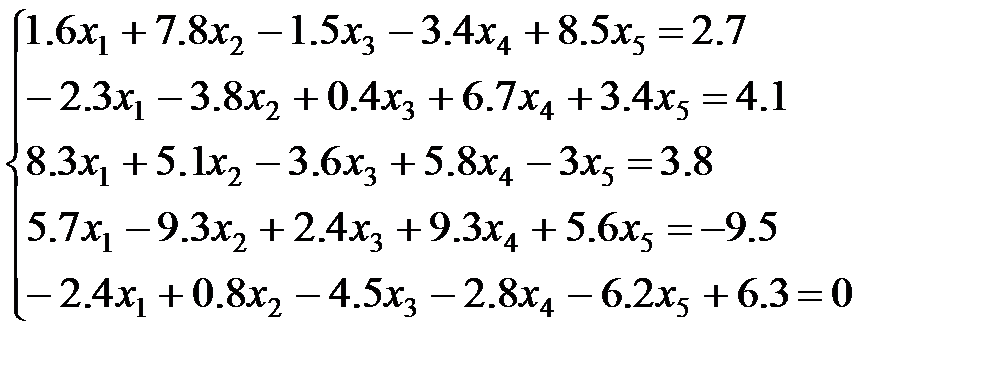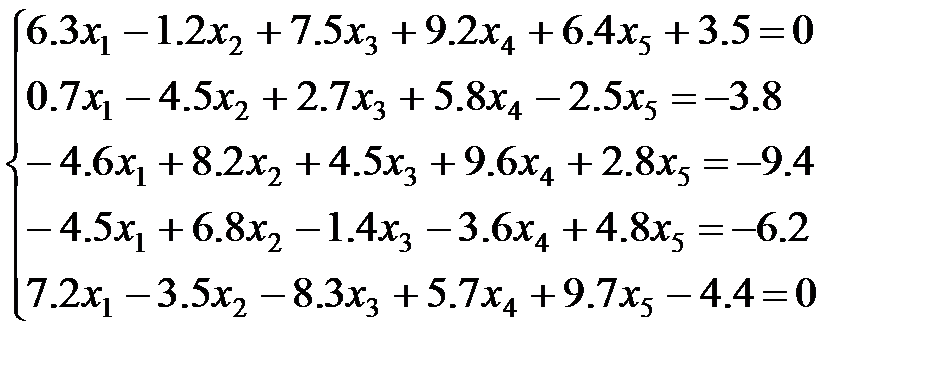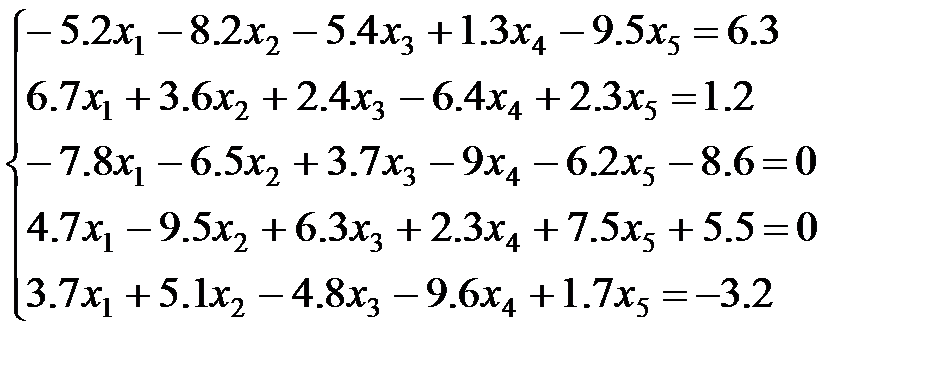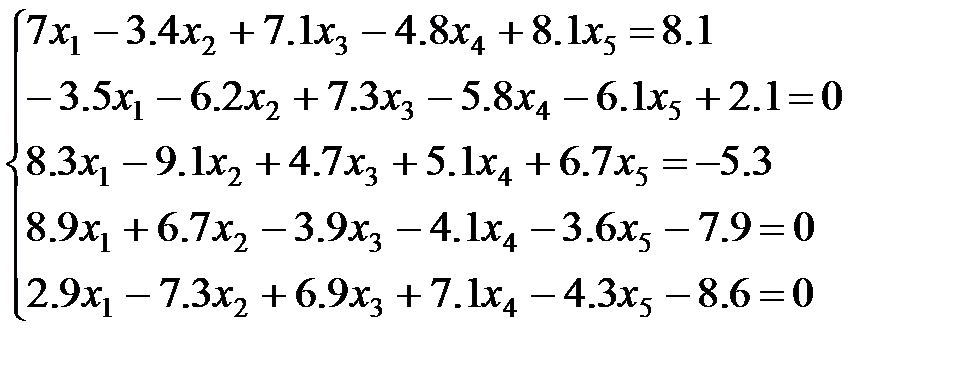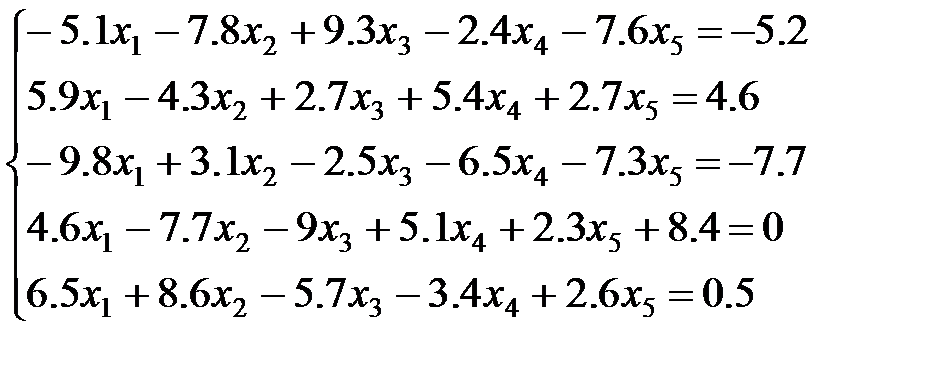Лабораторная работа №3
Цель работы:
· Знакомство с алгоритмом QR-разложения матрицы коэффициентов;
· Применение метода QR-разложения к решению систем линейных уравнений;
· Использование возможностей системы MATHCAD для выполнения QR-разложения.
Постановка задачи:
Найти решение системы линейных уравнений 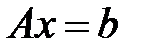 с помощью метода QR-разложения, где
с помощью метода QR-разложения, где
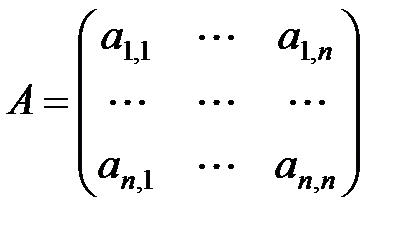 – матрица коэффициентов размера
– матрица коэффициентов размера 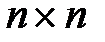 ,
,
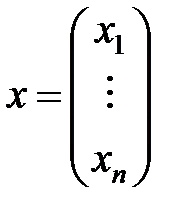 ,
, 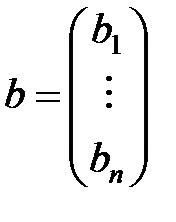 - столбец неизвестных и столбец свободных членов соответственно.
- столбец неизвестных и столбец свободных членов соответственно.
Описание метода:
Метод QR- разложения заключается в представлении матрицы коэффициентов 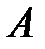 в виде произведения ортогональной матрицы
в виде произведения ортогональной матрицы 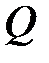 на верхнюю треугольную
на верхнюю треугольную 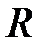 ,
, 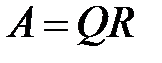 .
.
Пусть к шагу с номером  найдены матрицы
найдены матрицы 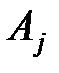 и
и  , такие, что матрица
, такие, что матрица 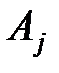 имеет вид
имеет вид 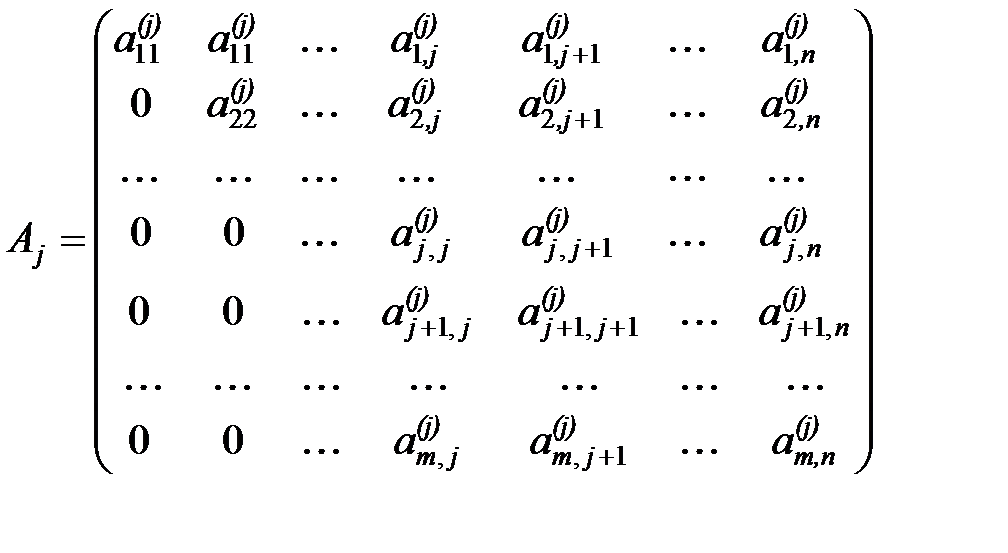 ,
,
 - ортогональная матрица и
- ортогональная матрица и 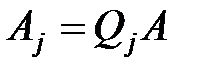 . На первом шаге
. На первом шаге  . Составим квадратную матрицу
. Составим квадратную матрицу
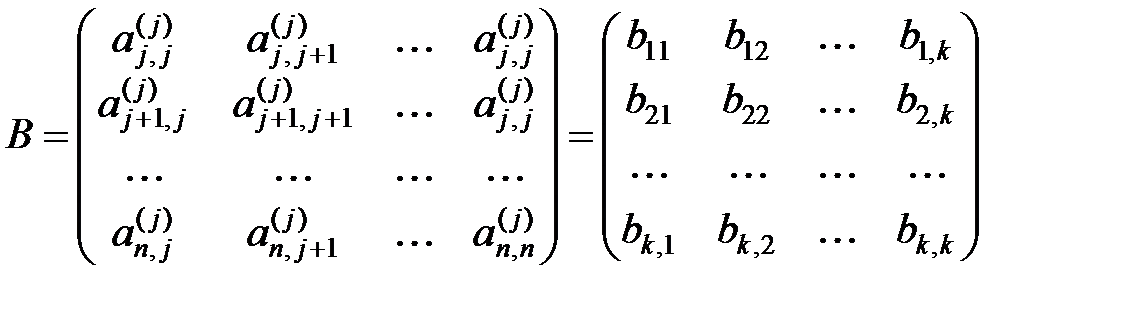 , где
, где 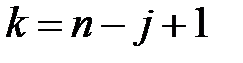 .
.
Пусть
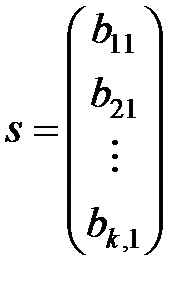 ,
, 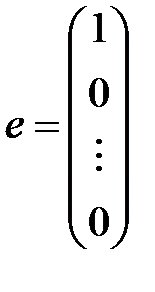 ,
, 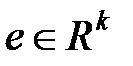 .
.
Возьмем число 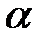 таким, что
таким, что 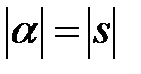 (
(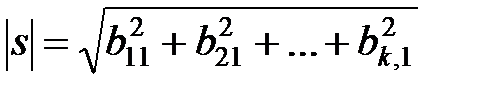 ), а знак числа
), а знак числа 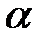 противоположен знаку числа
противоположен знаку числа 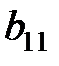 . Если
. Если  , то
, то 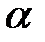 возьмем положительным. Пусть
возьмем положительным. Пусть 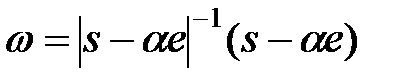 . Очевидно, что
. Очевидно, что 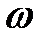 – единичный вектор. Положим
– единичный вектор. Положим 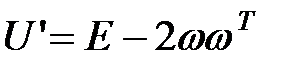 ,
, 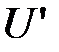 - ортогональная матрица (это легко проверить). Преобразование с матрицей
- ортогональная матрица (это легко проверить). Преобразование с матрицей 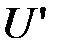 будет преобразованием отражения относительно плоскости с нормальным вектором
будет преобразованием отражения относительно плоскости с нормальным вектором 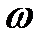 и будет вектор
и будет вектор 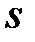 переводить в вектор
переводить в вектор 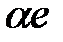 .
.
В произведении 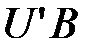 первый столбец получается умножением матрицы
первый столбец получается умножением матрицы 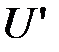 на столбец
на столбец 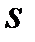 и поэтому станет равным
и поэтому станет равным
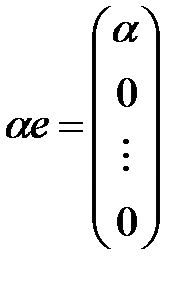 .
.
Образуем матрицу 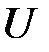 следующего вида
следующего вида
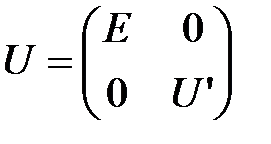 ,
,
где 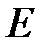 – единичная матрица порядка
– единичная матрица порядка 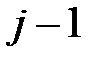 , при
, при 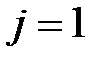 считаем, что
считаем, что 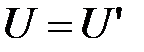 . Положим
. Положим 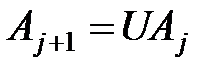 . В произведении
. В произведении 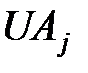 строки и столбцы номерами
строки и столбцы номерами 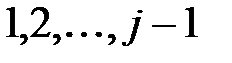 не изменятся, а элементы, у которых и номер строки, и номер столбца не меньше
не изменятся, а элементы, у которых и номер строки, и номер столбца не меньше  получаются, как элементы произведения
получаются, как элементы произведения 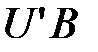 . Таким образом, матрица
. Таким образом, матрица 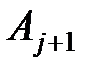 будет иметь вид
будет иметь вид
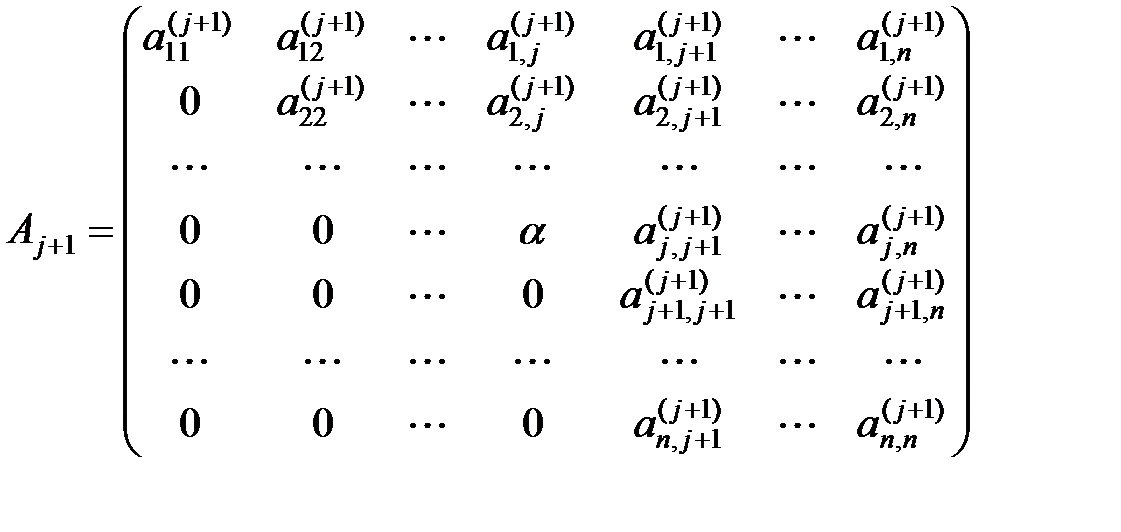 .
.
В этой матрице 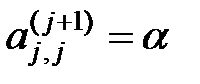 и под главной диагональю в столбцах
и под главной диагональю в столбцах  стоят нули. Учитывая, что
стоят нули. Учитывая, что 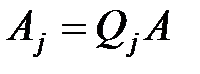 , получим
, получим 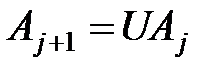 . Положим
. Положим 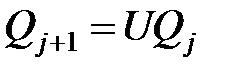 . Так как произведение ортогональных матриц является матрицей ортогональной, то матрица
. Так как произведение ортогональных матриц является матрицей ортогональной, то матрица 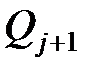 – ортогональная. Итак,
– ортогональная. Итак, 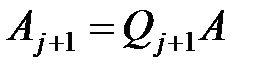 . Шаг с номером
. Шаг с номером  завершен. Выполнив
завершен. Выполнив  таких шагов, получим, что
таких шагов, получим, что 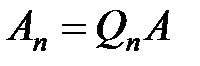 , где
, где 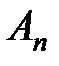 – верхняя треугольная. Отсюда
– верхняя треугольная. Отсюда 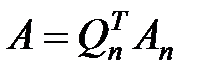 . Обратная к ортогональной матрице, т.е. транспонированная матрица, является ортогональной. Поэтому, обозначив
. Обратная к ортогональной матрице, т.е. транспонированная матрица, является ортогональной. Поэтому, обозначив 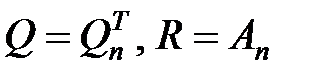 , получим требуемое QR-разложение.
, получим требуемое QR-разложение.
Преимуществом QR-разложения является то, что элементы матрицы R не могут сильно превышать по модулю элементы матрицы A. Действительно, 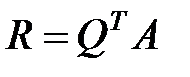 , т.е. каждый столбец матрицы R получается умножением ортогональной матрицы
, т.е. каждый столбец матрицы R получается умножением ортогональной матрицы 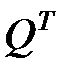 на соответствующей столбец матрицы A. Так как при умножении ортогональной матрицы на столбец вторая норма столбца не меняется, то нормы столбцов матрицы R совпадают с нормами соответствующих столбцов матрицы A. Норма каждого столбца ортогональной матрицы равна 1. Поэтому все элементы матрицы Q по модулю не больше 1.
на соответствующей столбец матрицы A. Так как при умножении ортогональной матрицы на столбец вторая норма столбца не меняется, то нормы столбцов матрицы R совпадают с нормами соответствующих столбцов матрицы A. Норма каждого столбца ортогональной матрицы равна 1. Поэтому все элементы матрицы Q по модулю не больше 1.
QR- разложение допустимо и для вырожденных матриц, если соответствующий нулевой столбец матрицы В считать уже получившимся на очередном шаге и сразу переходить к следующему шагу.
С помощью QR -разложения можно найти разложение прямоугольной матрицы коэффициентов. Если матрица А размера m×n, где 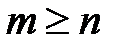 , то матрица
, то матрица 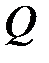 будет иметь размер
будет иметь размер 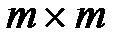 , а матрица
, а матрица  .
.
Недостатком метода служит то, что его реализация требует в два раза больше операций, чем LU-разложение. Кроме того QR-разложение требует дополнительную память для хранения матрицы Q, в то время, как в LU-разложении матрицы L и U могут формироваться в памяти компьютера на месте, занимаемом матрицей A. Впрочем, недостатки, как и преимущества, сказываются только при больших значениях n.
Ход лабораторной работы:
1. Ввести матрицу коэффициентов A (n × n) и столбец свободных членов b.
2. На первом шаге 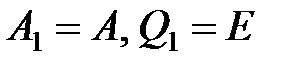 .
.
3. Пусть 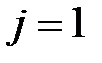 .
.
4. Создать матрицу 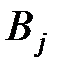 .
.
5. Создать векторы 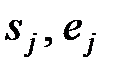 .
.
6. Найти число 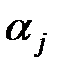 .
.
7. Найти единичный вектор 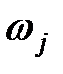 .
.
8. Найти матрицы 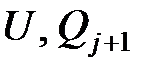 и
и 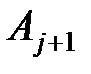 . Увеличить j на 1:
. Увеличить j на 1: 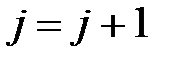 . Если
. Если 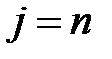 перейти к шагу 9, иначе к шагу 4.
перейти к шагу 9, иначе к шагу 4.
9. Ввести обозначение 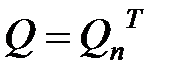 , создать матрицу
, создать матрицу  .
.
10. Найти решение системы 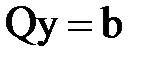 .
.
11. Найти решение системы 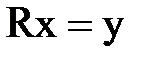 .
.
12. Выполнить проверку.
1) Для проверки разложения:
Вычислить произведение матриц QR, сравнить с матрицей A.
2) Для проверки решения:
Посмотреть выполняется ли равенство 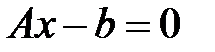 ?
?
Пример:
Найти решение системы линейных уравнений 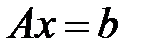 , где
, где

Получим QR-разложение матрицы коэффициентов:
На первом шаге 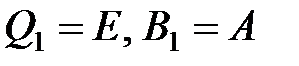 : :

|
Создаем векторы 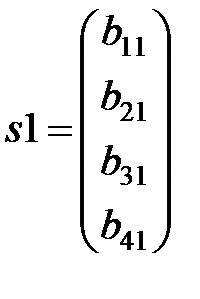 , , 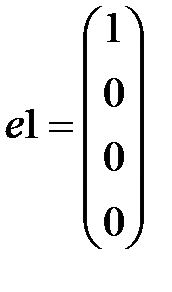 : :


|
Находим число 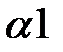 . Функция . Функция 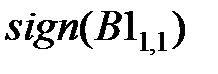 определяет знак элемента определяет знак элемента 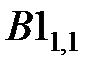 : :


|
Найдем единичный вектор 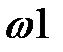 : :


|
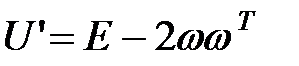 , , 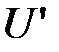 - ортогональная матрица: - ортогональная матрица:


|
Составляем матрицу 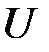 следующего вида следующего вида 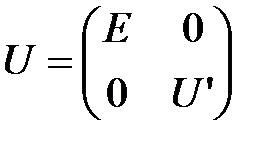 . На первом шаге . На первом шаге 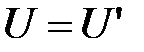 : :

|
Найдем матрицу  . Заметим, что матрица . Заметим, что матрица 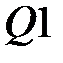 единичная, следовательно единичная, следовательно 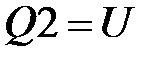 : :









|
Увеличиваем j на 1. Составляем матрицу 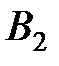 . Воспользуемся функцией Mathcad submatrix: . Воспользуемся функцией Mathcad submatrix:


|

|




|


|


|






|
Найдем матрицу 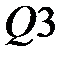 : :











 Матрица
Матрица 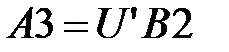 (см. описание метода): (см. описание метода):






|
Аналогично находим матрицы 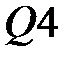 и и 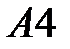 : :


|







|







|



















|
Составим матрицу 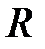 : :










|
Решим систему уравнений 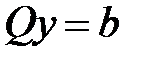 : :


|
Решив вторую систему  , получим: , получим:





|
Проверка:

|
Требования к отчету:
1. Отчет должен быть представлен в электронном или бумажном виде;
2. Отчет должен содержать:
· Расчеты и проверку.
3. Ответы на вопросы:
· Какова точность найденного решения;
· Преимущество метода QR-разложения по сравнению с
LU-разложением;
· Недостатки метода.
Задания для самостоятельной работы:
1 вариант:

2 вариант:
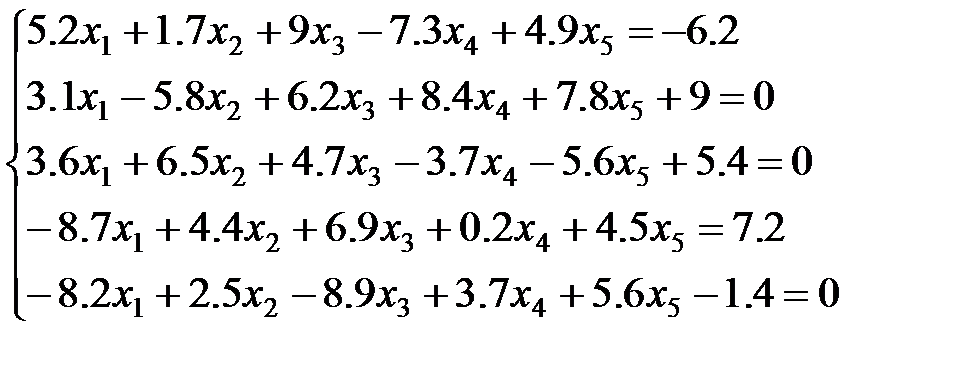
3 вариант:
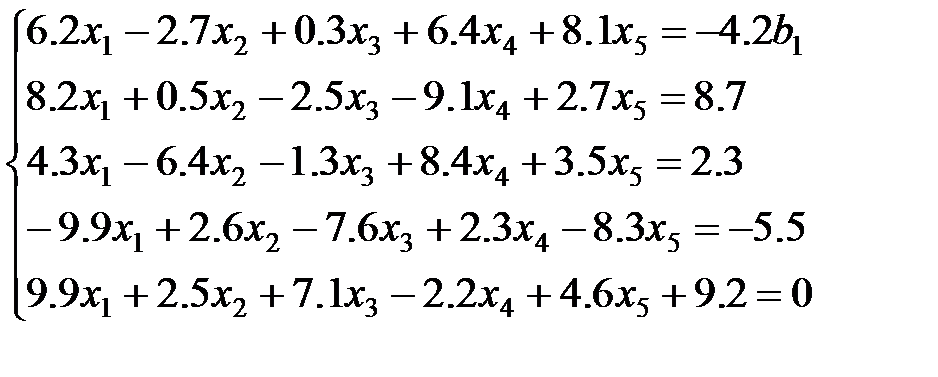
4 вариант:
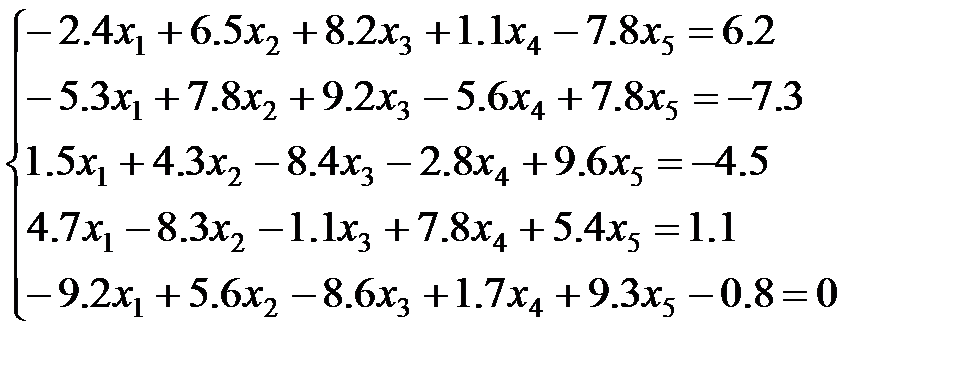
5 вариант:

6 вариант:
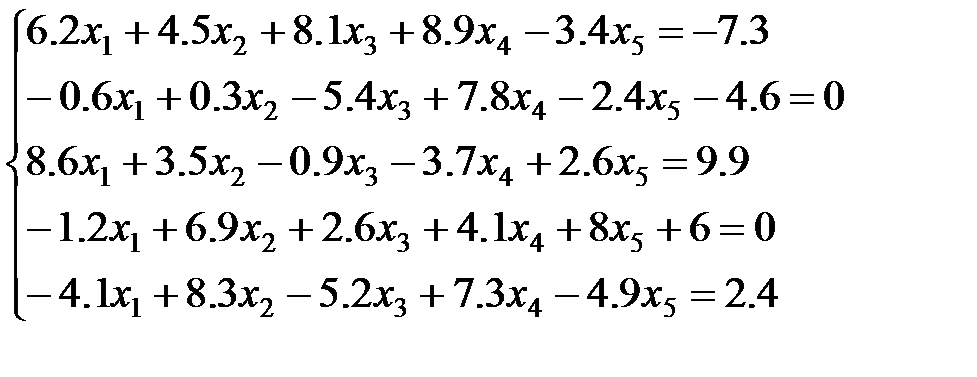
7 вариант:
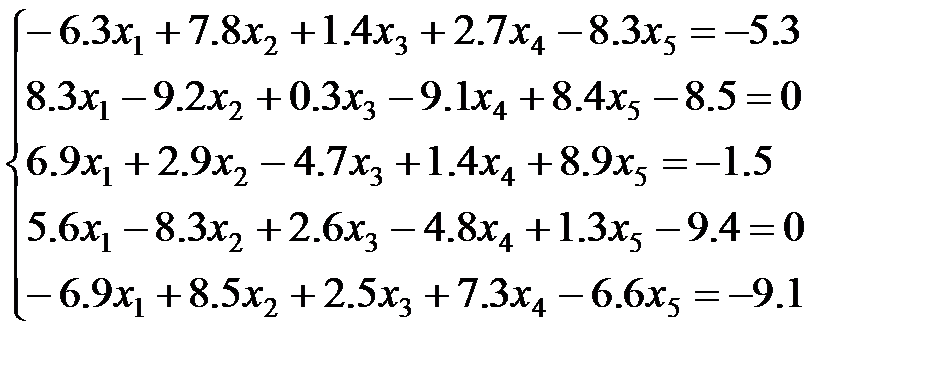
8 вариант:
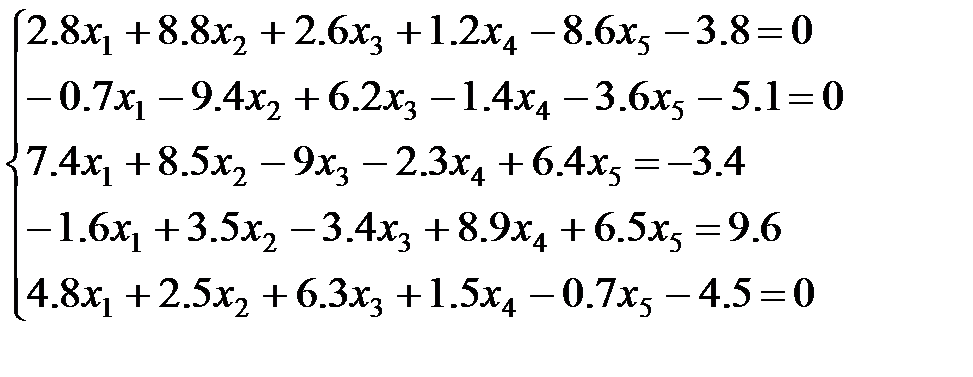
9 вариант:
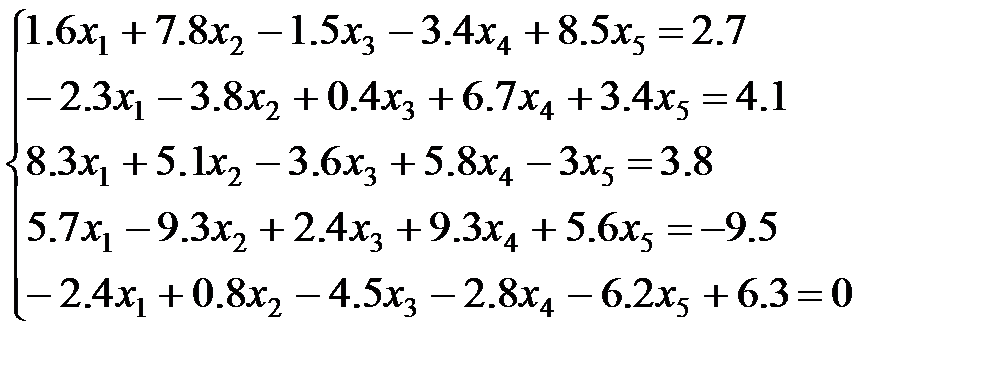
10 вариант:
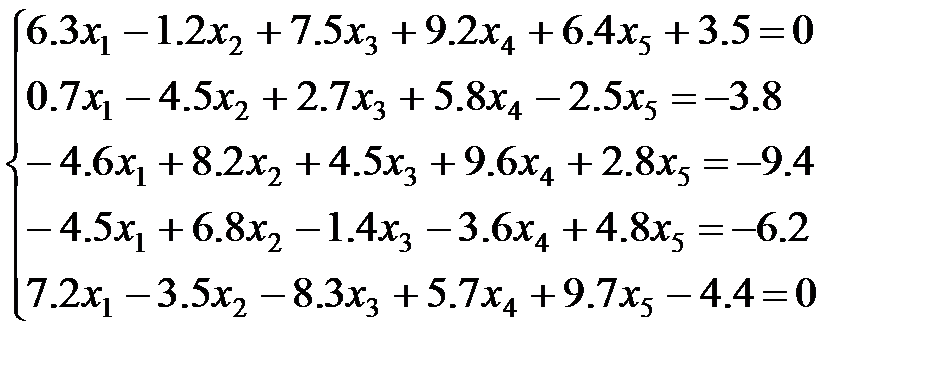
11 вариант:
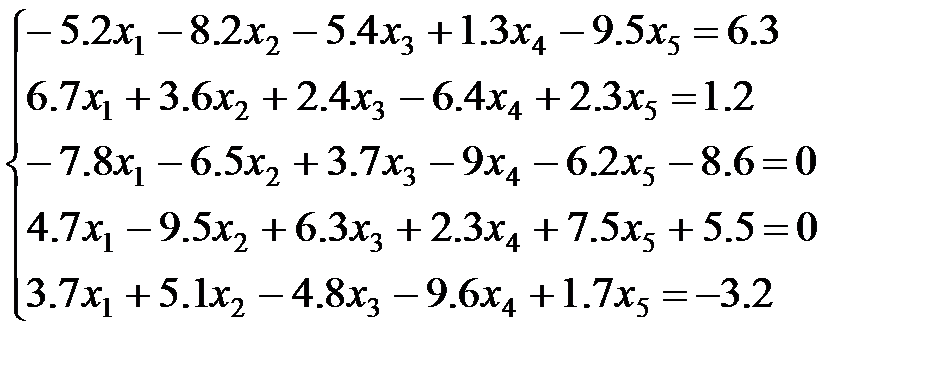
12 вариант:

13 вариант:
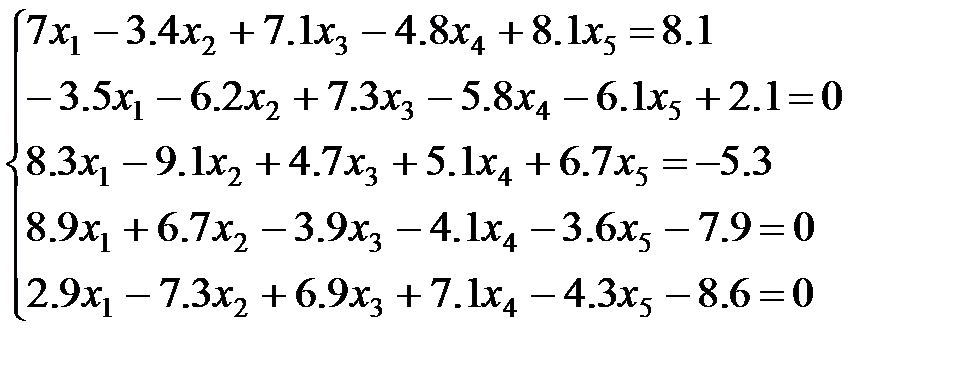
14 вариант:

15 вариант:
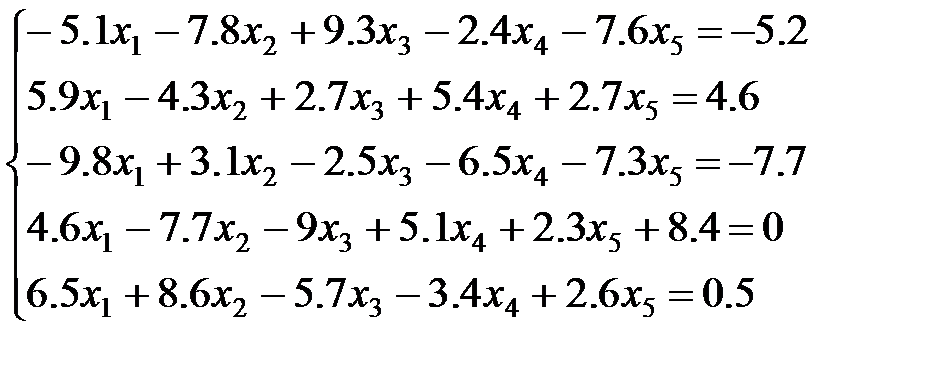

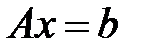 с помощью метода QR-разложения, где
с помощью метода QR-разложения, где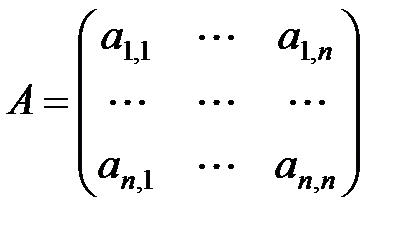 – матрица коэффициентов размера
– матрица коэффициентов размера 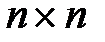 ,
,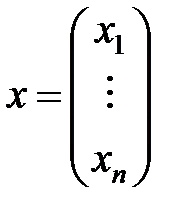 ,
, 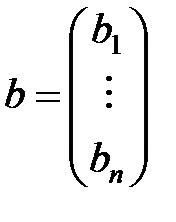 - столбец неизвестных и столбец свободных членов соответственно.
- столбец неизвестных и столбец свободных членов соответственно.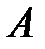 в виде произведения ортогональной матрицы
в виде произведения ортогональной матрицы 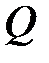 на верхнюю треугольную
на верхнюю треугольную 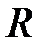 ,
, 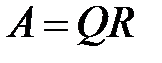 .
. найдены матрицы
найдены матрицы 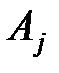 и
и  , такие, что матрица
, такие, что матрица 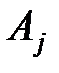 имеет вид
имеет вид 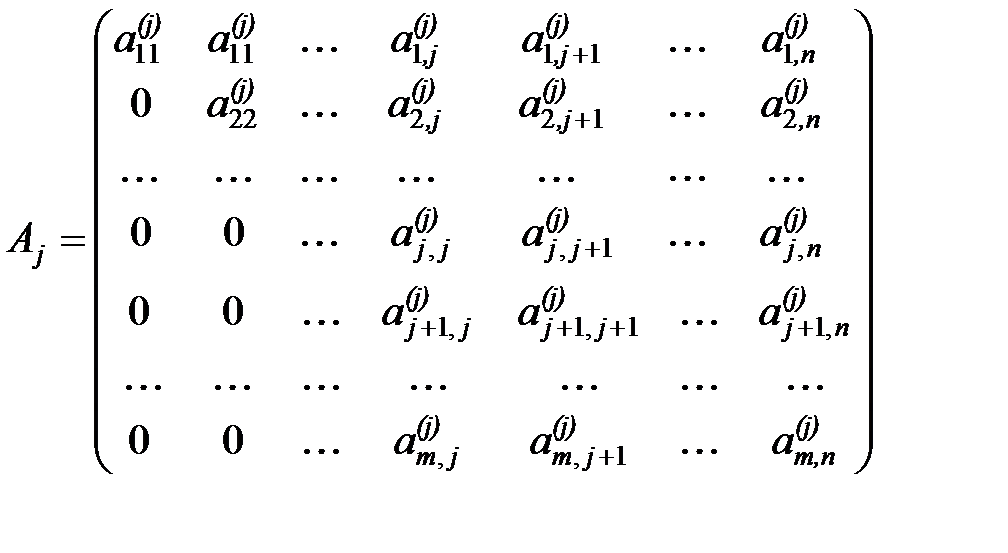 ,
, - ортогональная матрица и
- ортогональная матрица и 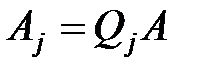 . На первом шаге
. На первом шаге  . Составим квадратную матрицу
. Составим квадратную матрицу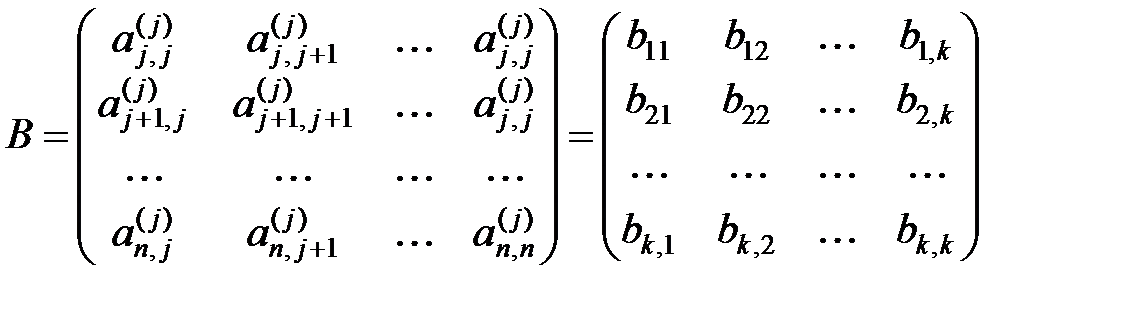 , где
, где 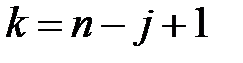 .
.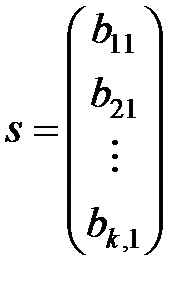 ,
, 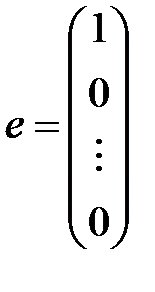 ,
, 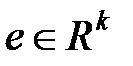 .
.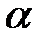 таким, что
таким, что 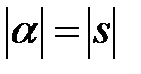 (
(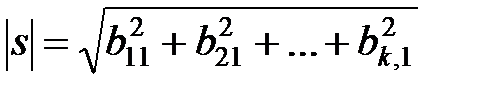 ), а знак числа
), а знак числа 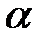 противоположен знаку числа
противоположен знаку числа 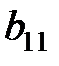 . Если
. Если  , то
, то 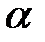 возьмем положительным. Пусть
возьмем положительным. Пусть 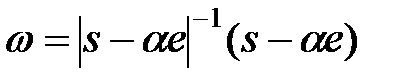 . Очевидно, что
. Очевидно, что 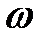 – единичный вектор. Положим
– единичный вектор. Положим 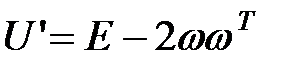 ,
, 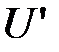 - ортогональная матрица (это легко проверить). Преобразование с матрицей
- ортогональная матрица (это легко проверить). Преобразование с матрицей 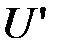 будет преобразованием отражения относительно плоскости с нормальным вектором
будет преобразованием отражения относительно плоскости с нормальным вектором 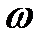 и будет вектор
и будет вектор 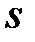 переводить в вектор
переводить в вектор 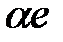 .
.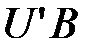 первый столбец получается умножением матрицы
первый столбец получается умножением матрицы 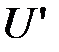 на столбец
на столбец 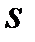 и поэтому станет равным
и поэтому станет равным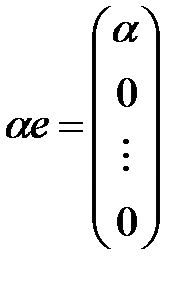 .
.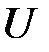 следующего вида
следующего вида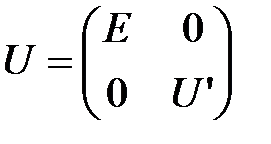 ,
,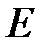 – единичная матрица порядка
– единичная матрица порядка 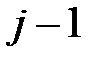 , при
, при 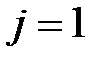 считаем, что
считаем, что 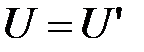 . Положим
. Положим 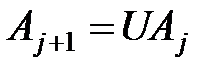 . В произведении
. В произведении 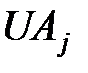 строки и столбцы номерами
строки и столбцы номерами 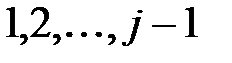 не изменятся, а элементы, у которых и номер строки, и номер столбца не меньше
не изменятся, а элементы, у которых и номер строки, и номер столбца не меньше  получаются, как элементы произведения
получаются, как элементы произведения 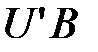 . Таким образом, матрица
. Таким образом, матрица 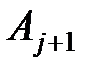 будет иметь вид
будет иметь вид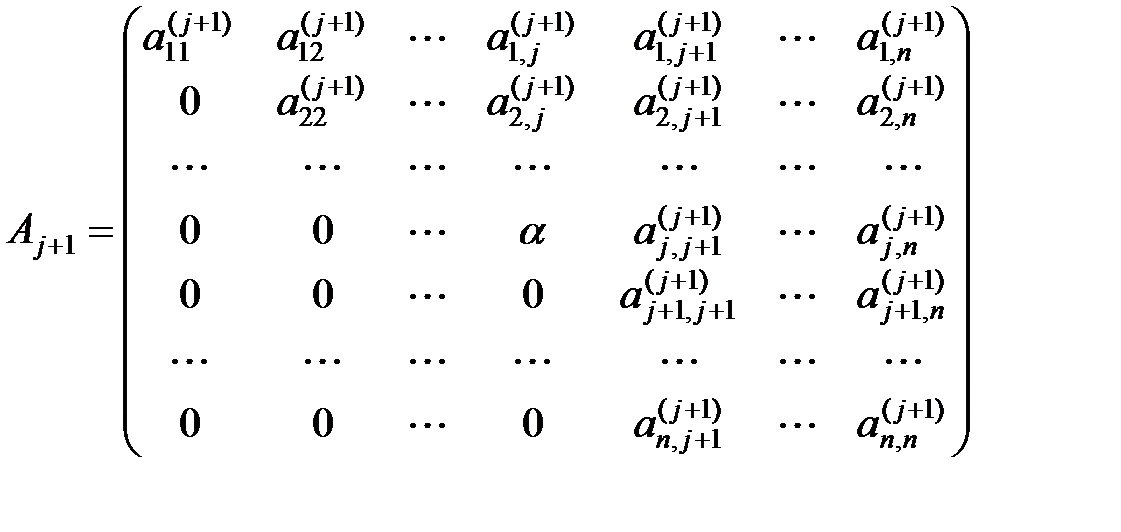 .
.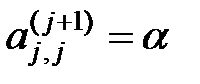 и под главной диагональю в столбцах
и под главной диагональю в столбцах  стоят нули. Учитывая, что
стоят нули. Учитывая, что 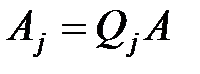 , получим
, получим 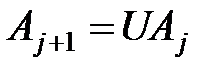 . Положим
. Положим 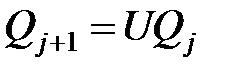 . Так как произведение ортогональных матриц является матрицей ортогональной, то матрица
. Так как произведение ортогональных матриц является матрицей ортогональной, то матрица 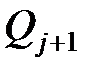 – ортогональная. Итак,
– ортогональная. Итак, 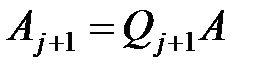 . Шаг с номером
. Шаг с номером  завершен. Выполнив
завершен. Выполнив  таких шагов, получим, что
таких шагов, получим, что 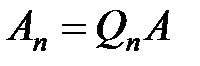 , где
, где 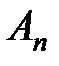 – верхняя треугольная. Отсюда
– верхняя треугольная. Отсюда 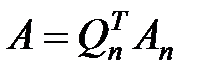 . Обратная к ортогональной матрице, т.е. транспонированная матрица, является ортогональной. Поэтому, обозначив
. Обратная к ортогональной матрице, т.е. транспонированная матрица, является ортогональной. Поэтому, обозначив 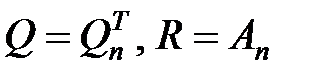 , получим требуемое QR-разложение.
, получим требуемое QR-разложение.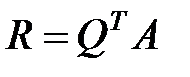 , т.е. каждый столбец матрицы R получается умножением ортогональной матрицы
, т.е. каждый столбец матрицы R получается умножением ортогональной матрицы 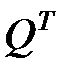 на соответствующей столбец матрицы A. Так как при умножении ортогональной матрицы на столбец вторая норма столбца не меняется, то нормы столбцов матрицы R совпадают с нормами соответствующих столбцов матрицы A. Норма каждого столбца ортогональной матрицы равна 1. Поэтому все элементы матрицы Q по модулю не больше 1.
на соответствующей столбец матрицы A. Так как при умножении ортогональной матрицы на столбец вторая норма столбца не меняется, то нормы столбцов матрицы R совпадают с нормами соответствующих столбцов матрицы A. Норма каждого столбца ортогональной матрицы равна 1. Поэтому все элементы матрицы Q по модулю не больше 1.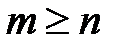 , то матрица
, то матрица 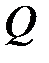 будет иметь размер
будет иметь размер 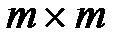 , а матрица
, а матрица  .
.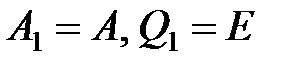 .
.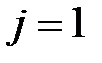 .
.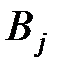 .
.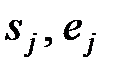 .
.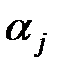 .
.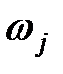 .
.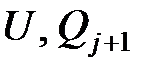 и
и 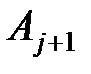 . Увеличить j на 1:
. Увеличить j на 1: 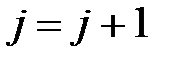 . Если
. Если 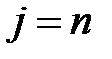 перейти к шагу 9, иначе к шагу 4.
перейти к шагу 9, иначе к шагу 4.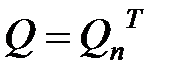 , создать матрицу
, создать матрицу  .
.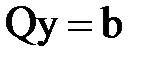 .
.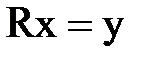 .
.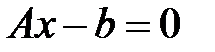 ?
?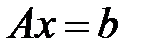 , где
, где
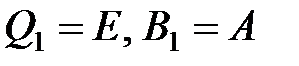 :
:

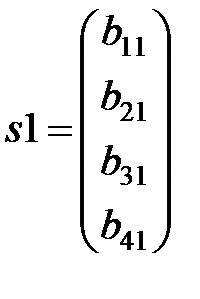 ,
, 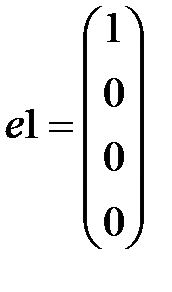 :
:


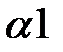 . Функция
. Функция 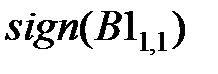 определяет знак элемента
определяет знак элемента 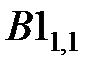 :
:


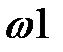 :
:


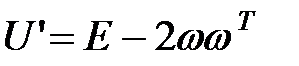 ,
, 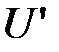 - ортогональная матрица:
- ортогональная матрица:


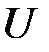 следующего вида
следующего вида 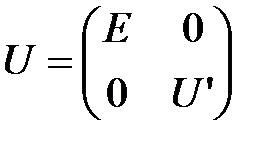 . На первом шаге
. На первом шаге 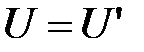 :
:

 . Заметим, что матрица
. Заметим, что матрица 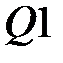 единичная, следовательно
единичная, следовательно 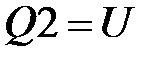 :
:









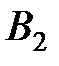 . Воспользуемся функцией Mathcad submatrix:
. Воспользуемся функцией Mathcad submatrix:

















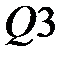 :
:











 Матрица
Матрица 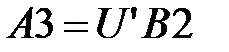 (см. описание метода):
(см. описание метода):






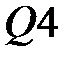 и
и 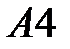 :
:



































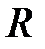 :
:










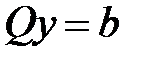 :
:


 , получим:
, получим: