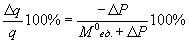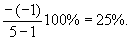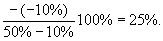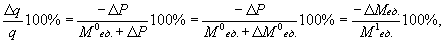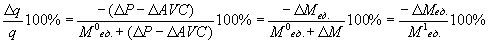МАКСИМАЛИЗАЦИЯ ПРИБЫЛИ ФИРМЫ, ОБЛАДАЮЩЕЙ МОНОПОЛЬНОЙ ВЛАСТЬЮ
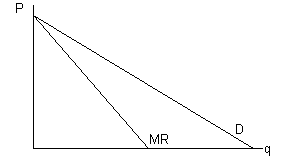
В самом начале этой темы говорилось, что кривая спроса на продукт фирмы, обладающей монопольной властью, имеет отрицательный наклон. Такая фирма может управлять ценой на свой товар, но тогда ей придется столкнуться с изменением величины спроса. Монополия – ценоискатель. Ее цель – установить такую цену, при которой ее прибыль будет максимальна. Общее правило максимизации прибыли – прибыль максимальна при выпуске, когда предельный доход равен предельным затратам – остается верным и для монополии. Разница лишь в том, для совершенно конкурентной фирмы линия предельного дохода (MR) горизонтальна и совпадает с линией рыночной цены, по которой эта фирма может продать любое количество своей продукции (см. рис. 5-1). Напротив, для монополии линия MR не горизонтальна и не совпадает с линией цены (кривой спроса). Для обоснования этого вспомним, что предельный доход есть приращение выручки при увеличении выпуска на одну единицу: MR=D TR/D q. Для примера исчисления предельного дохода возьмем самую простую функцию спроса на продукт монополии: P = 10 – q. Составим таблицу (табл. 5-3): Таблица 5-3. Предельный доход монополиста
Из данных таблицы следует, что если монополист снижает цену с 10 до 9, спрос увеличивается с 0 до 1. Соответственно, выручка возрастает на 9. Это и есть предельный доход, получаемый при выпуске дополнительной единицы продукции. Увеличение выпуска еще одну единицу приводит к повышению выручки еще на 7. И т.д. В таблице значения предельного дохода расположены не строго под значениями цены и спроса, а между ними. В данном случае приращения выпуска не являются бесконечно малыми, а потому предельный доход получается как бы "на переходе" от одной величины производства к другой. В тот момент, когда предельный доход достигает нуля (последняя единица выпуска вовсе не увеличивает выручку), выручка монополии достигает максимума. Дальнейшее увеличение производства ведет к падению выручки, т.е. предельный доход становится отрицательным. Данные таблицы позволяют сделать вывод, что величина предельного дохода, относящаяся к каждому значению выпуска (кроме нулевого), оказывается меньше соответствующего значения цены. Дело в том, что при выпуске дополнительной единицы продукции выручка увеличивается на цену этой единицы продукции. В то же время, чтобы продать эту дополнительную единицу выпуска, приходится снижать цену. Но по новой цене продаются не только последняя, но и все предыдущие единицы выпуска, прежде продававшиеся по более высокой цене. Поэтому монополист несет потери в выручке от снижения цены. Вычитая из выигрыша от роста выпуска потери от снижения цены, получаем величину предельного дохода, который оказывается, тем самым, меньше новой цены. Вернемся к таблице. Пусть монополист на прошлой неделе установил цену 7, продав по ней 3 ед. товара. Пытаясь увеличить выручку, он снижает на этой неделе цену до 6, что позволяет ему продать 4 ед. товара. Значит, от расширения выпуска на одну единицу монополист получает 6 ед. дополнительного дохода. Но от продажи первых 3 ед. товара он теперь получает только 18 ед. выручки, вместо 21 ед. на прошлой неделе. Потери монополиста от снижения цены равны, следовательно, 3. Поэтому предельный доход от расширения продаж при снижении цены составляет: 6 – 3 = 3 (см. таблицу 5-3). Можно строго доказать, что при линейной кривой спроса кривая MR также линейна, причем ее наклон вдвое больше наклона кривой спроса (рис. 5-8): Рис. 5-8. Кривые спроса и предельного дохода монополии
Соединим кривые спроса, предельного дохода (MR) и предельных затрат (МС) монополии на одном рисунке (рис. 5-9): Рис. 5-9. Максимизация прибыли фирмы, обладающей монопольной властью
Точка пересечения кривых MR и MC определяет выпуск (qm), при котором прибыль монополии максимальна. Предельный доход здесь равен предельным затратам. На кривой спроса находим монопольную цену, соответствующую этому выпуску (Pm). Говорят, что при такой цене (объеме выпуска) монополия находится в состоянии равновесия, ибо ей не выгодно ни повышать, ни снижать цену. Обращает на себя внимание то, что в условиях монопольного равновесия цена оказывается выше предельных затрат. В этом отличие от равновесия конкурентной фирмы: такая фирма выбирает выпуск, при котором цена в точности равна предельным затратам. Рассмотрим ряд практических вопросов функционирования фирмы, обладающей монопольной властью. Фирма хочет повысить свою прибыль. Ее интересует, может ли этому способствовать повышение или, напротив, снижение цены. Вопросы при этом могут быть поставлены так: "Насколько, как минимум, должен вырасти спрос при снижении цены, чтобы прибыль не упала?" или "Каково максимально допустимое сокращение спроса, чтобы фирма не проиграла в связи с ростом цены?" Пусть имеется ряд исходных данных, характеризующих деятельность фирмы:
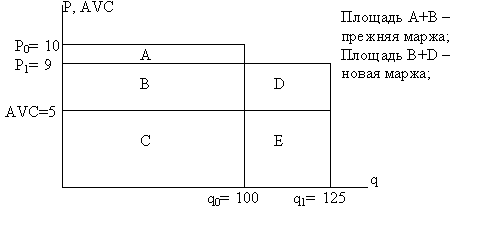
Предполагается снизить цену на 10%, т.е. до 9 руб. Необходимо рассчитать безубыточный прирост продаж (такой минимальный их прирост, который обеспечит сохранение прежней прибыли). Прибыль равна марже минус постоянные затраты (П = М – FC). Постоянные затраты не меняются с ростом выпуска. Следовательно, для достижения прежней прибыли маржа не должна упасть. Рассмотрим ситуацию графически (рис. 5-10): Рис. 5-10. Цена и сбыт фирмы
До снижения цены маржа составляла 500 руб. Цена упала с 10 до 9 руб. В результате при прежнем сбыте (100 шт.) маржа снизится до 400 руб. Значит, за счет роста сбыта маржа должна возрасти как минимум на 100 руб. (чтобы прибыль не упала). Такое станет возможным, если сбыт возрастет на 25 шт. (25%). Решим задачу в общем виде: Потерянная из-за снижения цены маржа составляет площадь А, которая равна: –D P×q. Приобретенная вследствие роста сбыта маржа составляет площадь D: (M0ед. + D P)×D q, где M0ед. – первоначальная удельная маржа. Поскольку площади А и D должны совпадать, то: (M0ед. + D P)×D q = –D P×q. Отсюда:
Левая часть уравнения – это и есть искомое процентное изменение сбыта. В нашем случае оно составляет:
Тот же результат получим, подставив вместо абсолютного изменения цены ее изменение в процентах:
При этом приведенные в знаменатели 50% представляют собой отношение первоначальной удельной маржи (5) к цене товара (10). Таким образом, 10%-ное снижение цены требует 25%-ного роста сбыта, чтобы прибыль осталась прежней. Помножив первоначальный сбыт (100) на найденное процентное изменение, рассчитываем минимально необходимый прирост сбыта в штуках (25). Вышеприведенную формулу легче понять, переписав ее так:
где M1ед. – новая удельная маржа (4 руб. в нашем примере). В результате получается, что необходимое процентное изменение сбыта должно соответствовать процентному изменению удельной маржи по отношению к новой удельной марже. Ту же формулу будем использовать для расчета максимально допустимого падения спроса в случае роста цены. Пусть наряду с изменением цены (упала на 1 руб.) меняются и средние переменные затраты. Предположим, AVC сократились до 4.5 руб. Тогда из-за снижения цены потери в марже при прежнем выпуске будут 50 руб. Значит, для сохранения прежней маржи выпуск должен возрасти на: 50/4.5 = 11.11 шт. В общем виде формула необходимого процентного изменения сбыта для сохранения прежней маржи (а значит, и прибыли) теперь выглядит так:
В нашем случае оно составляет:
Пусть фирма рассматривает вопрос об изменении (например – снижении) цены на один из своих товаров. Опираясь на только что приведенный анализ нетрудно рассчитать, насколько должен возрасти сбыт этого товара, чтобы фирма по крайней мере не проиграла в прибыли. Такой расчет, однако, очень часто нуждается в уточнении. Дело в том, что фирма, как правило, производит (продает) различные товары, которые зачастую являются взаимодополняющими. Это означает, что снижение цены на один из товаров может стимулировать рост сбыта не только его самого, но и других товаров. Зная о таком эффекте магазины, например, специально устанавливают заниженные (не покрывающие даже средние переменные затраты) цены на некоторые свои товары – т. н. "убыточные лидеры". Расчет делается на то, что привлеченные низкой ценой покупатели больше купят и товаров с "нормальными" ценами.
|