РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНОЙ ЦЕПИ.
I. Задание на расчет (цепь постоянного тока) Электрические цепи изображены на рис. 1. К цепям приложены напряжение E= 10 B, L= 1 мГн, С= 10 мкФ. Таблица содержит вариант задания, сопротивление постоянных резисторов, номер переменного резистора, тип переходного процесса и требуемую для расчета переходную электрическую величину (ток резистора, ток конденсатора, направление ветви с катушкой индуктивности). Требуется: 1) Подобрать такое значение сопротивление переменного резистора, которое обеспечивает заданный тип переходного процесса. 2)Рассчитать классическим методом переходной процесс для указанной электрической величины 3) Рассчитать тот же переходной процесс операторным методом, пользуясь найденными в п.2 начальными условиями. 4) Построить график изменения искомой величины в интервале от t=0 до t=3T0 в случае колебательного процесса и от t=0 до t=4 Примечание 1. В таблице буквами обозначены: А – апериодический, ПА – предельный апериодический и К – колебательные переходные процессы. II.Задание на расчет (цепь переменного тока) Электрическая цепь изображена на рис. 1. К цепи приложено напряжение Если не указано, то
Примечание 2. Номер варианта (трехзначное число) задается преподавателем. Предпоследняя и последняя цифры соответствуют номеру графика напряжения u(t) на рис. 2.
2. Теоритические положения классического метода. Переходной ток i(t) (или напряжение) в любой ветви линейной цепи находится в виде суммы двух слагаемых i(t)=iпр(t)+iсв(t), где iпр(t) – принужденная (вынужденная) составляющая тока; iсв(t) – его свободная составляющая. Принужденная составляющая определяется расчетом цепи в установившимся режиме любым из известных методов (по законам Кирхгофа, методом контурных токов, методом узловых напряжений и т.д.). Свободная составляющая тока возникает в результате перехода цепи от одного установившегося режима к другому, вызванного любым переключением в цепи. Для определенности предположим, что характеристическое уравнение имеет второй порядок. Тогда в зависимости от типа корней характеристическое уравнения, различается и тип переходного процесса и вид записи iсв(t). а) Апериодический процесс. Корни характеристического уравнения разные и действительные.
б) Предельный апериодический процесс. Корни кратные: р1=р2=р.
в) Колебательный процесс. Корни комплексно-сопряженные:
Для определения постоянных интегрирования А1 и А2 необходимо: 1) Записать переходной ток в виде:
или
2) Продифференцировать записанные выражения
3) Записать выражение тока и его производной для момента времени t=0+
В выражения (4- 6) входят начальные значения тока 1) Найти величины 2) Записать начальные условия для независимых электрических величин iL(0+)=iL(0-), uC(0+)=uC(0-). 3) Записать уравнения по законам Кирхгофа для цепи в момент времени t=0+, следующей за коммутацией. При этом не записывать уравнения по второму закону Кирхгофа для контура, содержащего ветвь с индуктивностью. 4) Подставить в уравнения Кирхгофа величины К сожалению, не существуют аналогичных общих приемов для определения начального значения производной искомого тока
получаются просто:
а значения uL(0+) и iC(0+) определяются путем решения уравнения Кирхгофа (см.п.4).
Последовательность расчета переходного процесса такова: 1) Определить iпр. 2) Записать характеристическое уравнение цепи и найти его корни. Для этого в после коммутационной схеме удалить источники (закоротить источники напряжения и разорвать источники тока), оборвать любую ветвь полученной схемы, записать выражение эквивалентного комплексного сопротивления Z(p)=0, что и определяет характеристическое уравнение. Найти корни характеристического уравнения. 3) Записать переходную величину в виде (1), (2) или (3). 4) Продифференцировать записанную величину
5) Записать систему (4), (5) или (6)
6) Найти 7) Найти 8) Подставить значения 9) Записать одно из выражений (1 - 3) для переходной величины с учетом найденных постоянных А1 и А2.
3. Пример расчета переходного процесса классическим методом. Пусть требуется определить переходную величину i(t) в цепи (рис. 3.) при воздействия на неё напряжения, форма которой указана на рис. 2. E=20B, L=1мГн, С=10мкФ, R2=10 Ом, R3=30Ом. В заданной схеме переменным резистором является R1. Найдем то значение его сопротивления, при которых возможно разные типы переходного процесса. Для этого исключаем источник и разрываем любую ветвь. Выгоднее разрывать ветвь, содержащую емкость. Эквивалентное комплексное сопротивление схемы (рис.4) относительно точек разрыва:
Множитель
Преобразуем его; определим коэффициенты уравнения при разных степенях р:
или, подставляя заданные значения параметров схемы, т.е.
Корни этого уравнения:
Для предельного апериодического процесса корни характеристического уравнения одинаковы. Это означает что подкоренное выражение (8) обращается в ноль: или
откуда т.е. Из двух значений R1 выбираем только физически реализуемое: R1=22 Ом. Подставляя это значение в (8), получаем корень характеристического уравнения, обеспечивающий предельный апериодический процесс:
При R1>22 Ом корни разные, что соответствует апериодическому переходному процессу. В частности, полагая R1=22 Ом, имеем
При R1<22 Ом корни характеристического уравнения комплексно – сопряженные, что соответствует колебательному процессу. Принимаем R1=10 Ом. Тогда
I. Апериодический процесс Расчет переходной величины i(t) разбиваем на два этапа. На первом этапе находим выражение для i(t) вследствие переключения напряжения u(t) от 0 до Е. На втором находи новое выражение для i(t), которое является результатом переключения напряжения u(t) от величины Е до 0 в момент 1. Первый этап. Находим принужденную составляющую тока iпр. В установившемся режиме в схеме действует напряжение u(t)=E=const, следовательно, и все токи постоянны. Индуктивное сопротивление равно нулю
2. Корни характеристического уравнения уже определены (см. (10)). 3. Записываем переходной ток i(t) в виде (1)
4. Дифференцируем это выражение
5. Записываем i(t) и di/dt для t=0+
6. При t<0, в частности, при t=0- u(t)=0, откуда iL(0-)=0, uC(0-)=0, а также i(0-)=0. Схема для расчета начального значения тока i(0+) имеет вид рис. 6 (послекоммутационная схема). По законам коммутации iL(0+)=iL(0-)=0, uC(0+)=uC(0-)=0. Записываем уравнение по законам Кирхгофа
откуда а также 7. Находим
Так как dE/dt=0, то
Производную напряжения uC(t), легко определить через ток iC(t). Исходя из того, что
При t=0+:
8. Находим постоянные интегрирования, подставляя в систему (13) начальные значения i(0+) и
откуда А1=0,1567; А2=-0,0067. 9. Записываем выражение для переходного тока
Второй этап. Определяем время окончания действия напряжения u(t)=E:
Вводим новую переменную 1/. Так как u(t/)=0 при t/>0, то iпр(t/)=0. 2/. Корни характеристического уравнения остались без изменения, т.к. параметры схемы прежние. 3/. Переходной ток при t/>0 имеет вид
4/. 5/. 6/. Схема до вторичного переключения имеет вид рис. 7 (докумматационная схема). Переходной ток (16) в момент
Находим значения независимых величин iL и uC в момент t/=0/-, составляя системы уравнений для схемы рис. 7,
В этой системе три неизвестных: iL(0/-), uC(0/-), iC(0/-), поэтому требуется дополнительная связь для их однозначного определения. Находим эту связь, дифференцируя уравнение E=(R3+R2)i(t/)+uС(t/), составленное по 2-му закону Кирхгофа:
Величину
Выражением duC/dt/ через ток iC(t/):
подставляем в (18) и получаем
Решаем систему (17):
По законам коммутации iL(0/+)=iL(0/-)=0,1302 A, uC(0/+)=uC(0/-)=4,62 B.
Схема для расчета начального значения переходной величины i(0/+) имеет вид рис. 8 (послекоммутационная схема). По 2-му закону Кирхгофа (R3+R2)i(0/+)+uC(0/+)=0, откуда 7/. По 1-му закону Кирхгофа iC(0/+)=i(0/+) - iL(0/+)= - 0,0924- 0,1302= - 0,2226A. Аналогично (15) получаем
8/.
А/1=-0,0884, А/2=-0,003996.
9/.
График переходной величины, построенный по выражениям (16) и (19), приведен на рис. 9.
2. Предельный апериодический процесс Первый этап. Напряжение переключается от величины u=0 до u=E. 1.Согласно рис. 5
2.Корни характеристического уравнения вычислены (см. (9)). 3.Переходной ток ищем в виде (2):
4.
5.
6.7. Расчет начальных значений i(0+) и
8. Записываем систему уравнение для определения постоянных интегрирования
Решаем её определяем: А1=0,1222, А2=666,666. 9.
Второй этап.
В момент Вводим новую переменную 1/. 2/. Корень характеристического уравнения прежний: р=-12000 с-1. 3/. 4/.
6/. Согласно (21) и (20), находим значения
Дальнейшие вычисления аналогичны п.6 предыдущего раздела и касаются рис. 7:
Расчет схемы рис. 8:
7/.
8/.
9/. График переходного тока i(t), построенный согласно выражениям (21) и (22), приведен на рис. 10.
3. Колебательный процесс
Первый этап. 1. См. рис. 5.
2. Корни характеристического уравнения определены (см. (11)). 3. Переходную величину имеем в виде (3)
4.
5.
6.7. До первого переключения напряжения независимые величины имеют нулевые значения: iL(0-)=0, uC(0-)=0. Расчет начального значения производим по схеме рис. 6. Уравнения, составленные по законам Кирхгофа, те же, что и в п.п.6 и 7 разделов 1 и 2, т.е. (14), в которые не входит параметр R1. Тогда без изменения остаются и начальные значения:
8. Подставляем эти значения в систему (25):
откуда А1=0,06667, А2=-0,04364. 9. Искомое решение (23) принимает вид:
Это выражение можно привести к единой тригонометрической функции, например, к синусоидальной. Находим амплитуду приведенной синусоиды:
Начальную фазу определить легко, если предварительно спроецировать амлитуды А1, А2 на комплексную плоскость (рис. 11).
+j
A A1
A2 0
Рис. 11
Следовательно,
Второй этап. Находим время 2-го переключения напряжения:
Вводим новую переменную 1/. Так как 2/. Структура и параметры схемы не изменились, поэтому и корни характеристического уравнения остались прежними:
3/. 4/. Выражение для di/dt аналогично (24). 5/.
6/. Подставляя в (26) и (24) значение
Далее повторяем расчет схемы рис. 7 в п.6 раздела 1 и 2:
По законам коммутации
Рассчитываем схему рис. 8:
7/.
8/. Система (28) приобретает вид:
Ее решение: 9/.
График переходной величины i(t), построенный по выражениям (27) и (28) приведен на рис. 12.
4. Теоретическое положение операторного метода
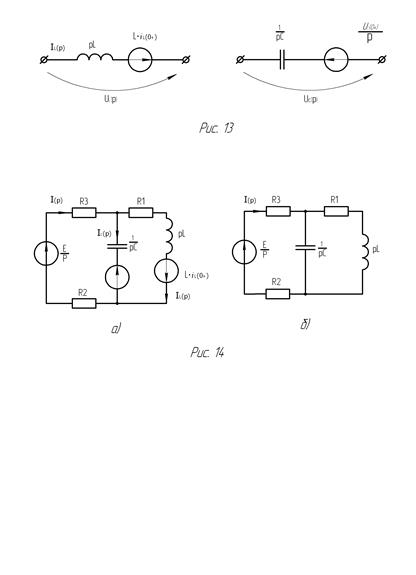
При расчете переходной величины i(t) отыскивается ее операторное изображение I(p) (операторный ток). Операторный ток определяется любым из известных методов расчета сложных цепей по операторной схеме замещения. Эта схема содержит операторные сопротивления элементов, операторного изображение внешних источников энергии (для постоянных источников E(p)=E/p и внутренние источники энергии, включенные параллельно или последовательно с реактивными элементами (рис.13). Найденный операторный ток I(p) представляется в виде отношения полиномов
Переходная величина i(t) находится по теореме разложения
где pk - корни характеристического уравнения
F1p(k) – значение полинома F1(p) при подстановке в него pk;
Теорема разложения в виде (30) применяется в предположении, что все корни характеристического уравнения F2(p)=0 разные (действительные или комплексно сопряженные). В частных случаях эта формула упрощается. Наиболее характерные из них следующие. 1. Один корень нулевой, два других p1 и p2 - равные действительные.
2. Один корень нулевой и один корень
3. Один корень нулевой, два других – комплексно -сопряженные.
5. Пример расчета переходного процесса операторным методом Пусть требуется вычислить ту же переходную величину i(t), что и в предыдущем примере. Изображаем операторную схему замещения (рис. 14. а). Из-за нулевых начальных условий для независимых величин (iL(0+)=0, uC(0+)=0) она упрощается (рис. 14, б). Находим эквивалентное операторное сопротивление этой схемы
и операторный ток
Делим числитель и знаменатель на коэффициент при старшей степени р полинома знаменателя:
1. Апериодический процесс Подставляя в (34) значения параметров схемы и величину Е=20В, получаем:
р1=-6202с-1, р2=-25798с-1. Применяем теорему разложения в форме (31). Проводим необходимые вычисления:
Следовательно,
что совпадает с выражением (16).
2. Предельный апериодический процесс
Операторный ток (34) видоизменяется:
р1=р2=-12000с-1. Воспользуемся теоремой разложения в форме (32). Предварительные вычисления:
Тогда
что совпадает с выражением (21).
3. Колебательный процесс
Применяем теорему разложения в форме (38). Производим необходимые для этого вычисления:
Следовательно,
что совпадает с выражением (27).
|

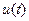 , которое меняется от
, которое меняется от  до
до  . График приведен на рис. 2. Для всех вариантов задания:
. График приведен на рис. 2. Для всех вариантов задания: в случае апериодических процессов.
в случае апериодических процессов. . Определить требуемое значение электрической величины при закорачивании сопротивления (указано в задании),
. Определить требуемое значение электрической величины при закорачивании сопротивления (указано в задании),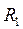 во всех схемах, кроме схемы на рис.7 - закорачивается сопротивление
во всех схемах, кроме схемы на рис.7 - закорачивается сопротивление  , на рис.8 - закорачивается сопротивление
, на рис.8 - закорачивается сопротивление 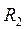 . Частота тока f =500Гц. Построить график изменения искомой величины.
. Частота тока f =500Гц. Построить график изменения искомой величины. .
.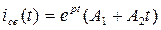 .
.
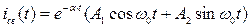
 , (1)
, (1) (2)
(2)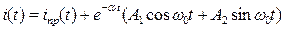 . (3)
. (3) ,
,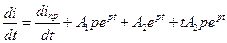 ,
,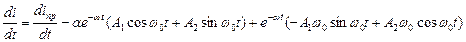 .
. (4)
(4)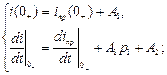 (5)
(5) (6)
(6) и его производной
и его производной 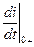 . Для вычисления
. Для вычисления 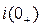 необходимо:
необходимо: и
и  путем расчета установившегося процесса в цепи до коммутации (переключения).
путем расчета установившегося процесса в цепи до коммутации (переключения).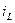 и
и 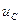 ,пользуясь законами коммутации.
,пользуясь законами коммутации. и
и 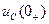 . Решая уравнения, найти
. Решая уравнения, найти 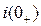 .
.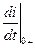 . Рекомендуется записать уравнения Кирхгофа для произвольного t после коммутации и продифференцировать их, пытались получить di/dt через известные величины. Следует иметь в виду, производные независимых величин
. Рекомендуется записать уравнения Кирхгофа для произвольного t после коммутации и продифференцировать их, пытались получить di/dt через известные величины. Следует иметь в виду, производные независимых величин
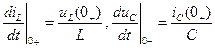 ,
, относительно точек разрыва, множитель
относительно точек разрыва, множитель  заменить оператором p. Полученное таким образом выражение приравнять к нулю:
заменить оператором p. Полученное таким образом выражение приравнять к нулю:
 (7)
(7) .
.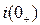 и
и  в систему (7) и решить ее относительно А1 и А2.
в систему (7) и решить ее относительно А1 и А2.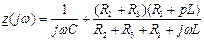 .
.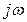 заменяем оператором p, получаем таким образом характеристическое уравнение.
заменяем оператором p, получаем таким образом характеристическое уравнение. .
.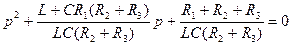 ,
, ,
,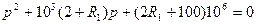 .
.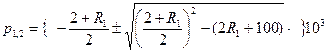 (8)
(8) ,
, ,
, ,
,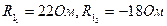 .
.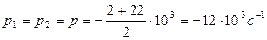 . (9)
. (9)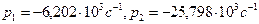 . (10)
. (10)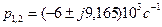 . (11)
. (11) .
. , а емкостное - бесконечности
, а емкостное - бесконечности 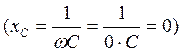 . Поэтому расчетная схема имеет вид рис. 5.
. Поэтому расчетная схема имеет вид рис. 5.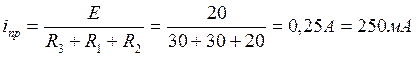 .
. .
.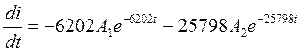 . (12)
. (12) (13)
(13) (14)
(14)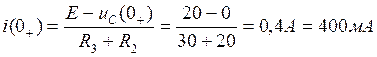 ,
, .
. . Для этого дифференцируем уравнение, записанное по 2-му закону Кирхгофа
. Для этого дифференцируем уравнение, записанное по 2-му закону Кирхгофа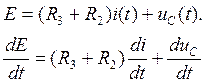 .
.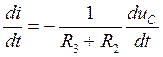 .
.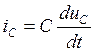 , имеем
, имеем .
.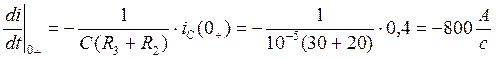 .
.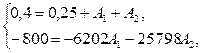
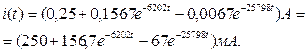 (16)
(16)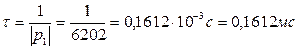 .
. . Тогда моменту переключения напряжения от значения Е до значения 0 соответствует t/=0. Для определения переходной величины i(t/) повторяем вычисления аналогичные предыдущим.
. Тогда моменту переключения напряжения от значения Е до значения 0 соответствует t/=0. Для определения переходной величины i(t/) повторяем вычисления аналогичные предыдущим. .
. .
.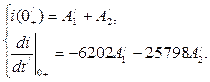
 .
. (17)
(17) . (18)
. (18) вычисляем, пользуясь выражением (12):
вычисляем, пользуясь выражением (12):
 ,
, .
.
 .
. .
.

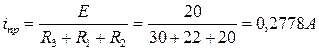 .
.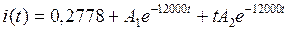 .
. . (20)
. (20)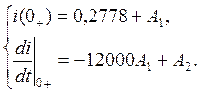
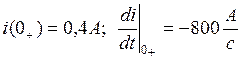 .
.
 (21)
(21)
 происходит переключение напряжения от и=Е до и=0:
происходит переключение напряжения от и=Е до и=0: .
. .
.
 .
.
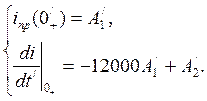
 до второго переключения:
до второго переключения: .
.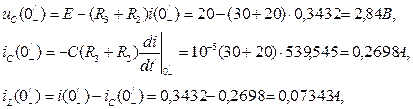

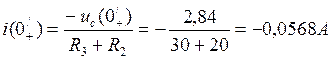 .
.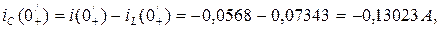


 (22)
(22)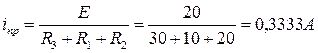 .
.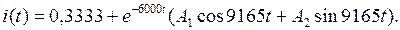 (23)
(23)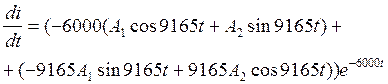 (24)
(24)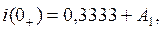
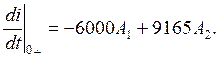 (25)
(25)

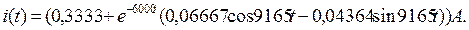 (26)
(26) .
.
 +1
+1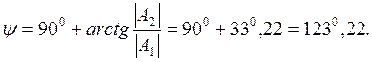
 (27)
(27) .
. , то iпр(t/)=0.
, то iпр(t/)=0.
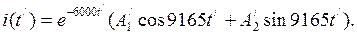
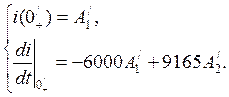 (28)
(28) , находим:
, находим:
 .
.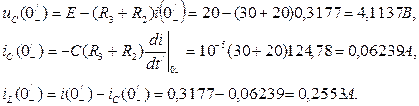



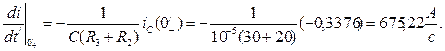
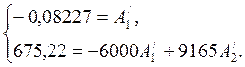
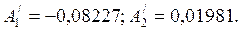
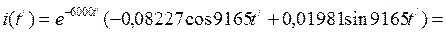
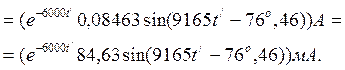 (29)
(29)
 , (30)
, (30)
 – производная полинома F2(p) по переменной p;
– производная полинома F2(p) по переменной p;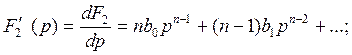
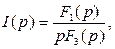
 (31)
(31)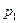 кратности 2.
кратности 2.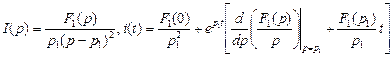 (32)
(32) (33)
(33)
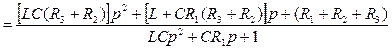
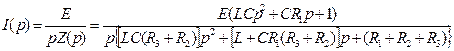 .
. . (34)
. (34)


 ,
,


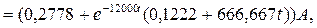
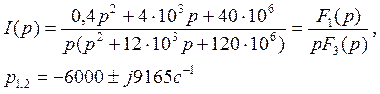

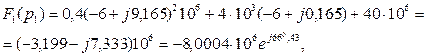
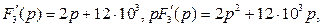
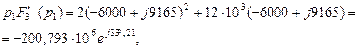
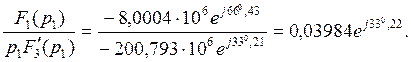
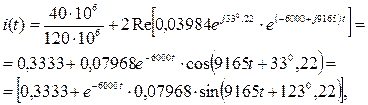

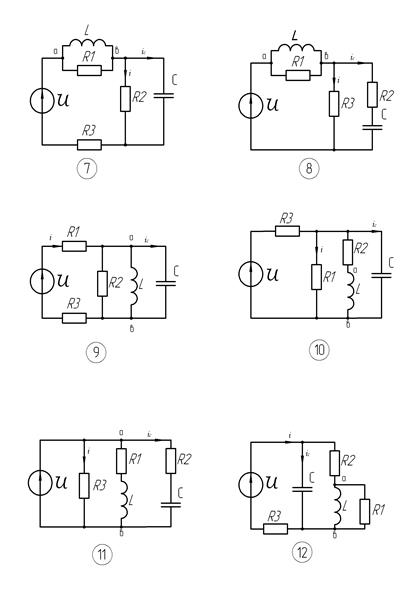
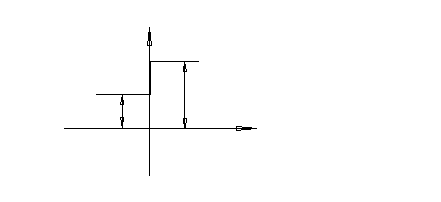 Рис.2
Рис.2