Момент силы относительно оси.
Чтобы перейти к решению задач статики для случая произвольной пространственной системы сил, необходимо ввести еще понятие о моменте силы относительно оси. Момент силы относительно оси характеризует вращательный эффект, создаваемый силой, стремящейся повернуть тело вокруг данной оси. Рассмотрим твердое тело, которое может вращаться вокруг некоторой оси z (рис. 39).
Рис.39 Пусть на это тело действует сила Для силы же В результате приходим к следующему определению: моментом силы относительно оси называется скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.
Рис.40 Момент будем считать положительным, если с положительного конца оси z поворот, который сила Из чертежа (рис.40) видно, что при вычислении момента плоскость ху можно проводить через любую точку оcи z. Таким образом, чтобы найти момент силы относительно оси z (рис. 40) надо: 1) провести плоскость ху, перпендикулярную к оси z (в любом месте); 2) спроектировать силу 3) опустить из точки О пересечения оси с плоскостью перпендикуляр на направление 4) вычислить произведение 5) определить знак момента. При вычислении моментов надо иметь в виду следующие частные случаи: 1) Если сила параллельна оси, то ее момент относительно оси равен нулю (так как 2) Если линия действия силы пересекает ось, то ее момент относительно оси также равен нулю (так как h = 0). Объединяя оба случая вместе, заключаем, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости. 3) Если сила перпендикулярна к оси, то ее момент относительно оси равен произведению модуля силы на расстояние между силой и осью. Рис. 3.4. Пример 4. Определим моменты сил
Рис.41
Моменты силы
Моменты сил В тех случаях, когда вектор силы направлен под углом к осям, полезно разложить вектор силы на составляющие параллельные осям и, затем, находить сумму моментов этих составляющих. Так моменты силы
И силы
|

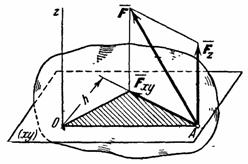
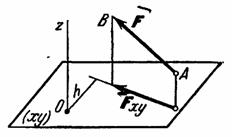
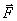 ,приложенная в точке А. Проведем через точку А плоскость ху, перпендикулярную оси z, и разложим силу
,приложенная в точке А. Проведем через точку А плоскость ху, перпендикулярную оси z, и разложим силу 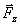 , параллельную осиz, и
, параллельную осиz, и 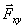 , лежащую в плоскости ху (
, лежащую в плоскости ху (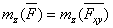 , где символ
, где символ 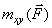 ) обозначает момент силы
) обозначает момент силы  или, согласно предыдущему равенству,
или, согласно предыдущему равенству, 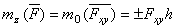 .
.
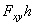 ;
; ).
). и
и 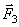 относительно осей (рис.41).
относительно осей (рис.41).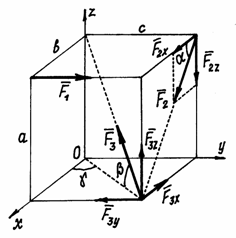
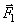 находятся просто:
находятся просто: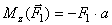 ;
; ;
;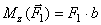 .
. и
и 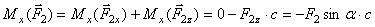 ;
;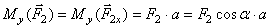 ;
; 
 .
.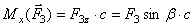 ;
;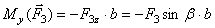 ;
; (линия действия силы
(линия действия силы 


