Зависимость между моментами силы относительно центра и относительно оси.
Пусть на тело действует приложенная в точке А сила
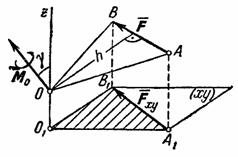
Рис.42 Проведем теперь через любую точку O 1 на оси z плоскость ху, перпендикулярную к оси; проектируя силу Но треугольник О 1 А 1 В 1 представляет собою проекцию треугольника ОАВ на плоскость ху. Угол между плоскостями этих треугольников равен углу между перпендикулярами к плоскостям, т. е. равен Умножая обе части этого равенства на 2 и замечая, что удвоенные пощади треугольников О 1 А 1 В 1 и ОАВ равны соответственно m z( Так как произведение
В результате мы доказали, что между моментом силы относительно оси и ее моментом относительно какого-нибудь центра, лежащего на этой оси, существует следующая зависимость: момент силы
|
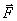(рис. 42). Проведем какую-нибудь ось z и возьмем на ней произвольную точку О. Момент силы 
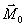перпендикулярным плоскости ОАВ, причем по модулю 
.
.
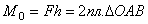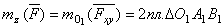. Тогда, по известной геометрической формуле, 
.
.
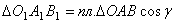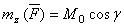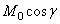дает проекцию вектора 
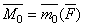на ось z, то равенство можно еще представить в виде
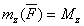или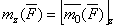 
.
