Чтобы перейти к решению задач статики для системы сил, как угодно расположенных в пространстве, оказывается необходимым несколько уточнить и расширить ряд введенных ранее понятий. Начнем с понятия о моменте силы.
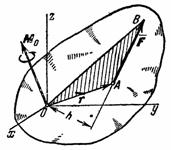
Рис.37
1. Изображение момента вектором. Момент силы 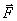 относительно центра О (см. рис. 37) как характеристика ее вращательного эффекта определяется следующими тремя элементами:
относительно центра О (см. рис. 37) как характеристика ее вращательного эффекта определяется следующими тремя элементами:
1) модулем момента, равным произведению модуля силы на плечо, т. е. 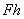 ; 2) плоскостью поворота ОАВ, проходящей через линию действия силы
; 2) плоскостью поворота ОАВ, проходящей через линию действия силы 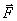 и центр О; 3) направлением поворота в этой плоскости. Когда все силы и центр О лежат в одной плоскости, необходимость задавать каждый раз плоскость поворота ОАВ отпадает, и момент можно определять как скалярную алгебраическую величину, равную
и центр О; 3) направлением поворота в этой плоскости. Когда все силы и центр О лежат в одной плоскости, необходимость задавать каждый раз плоскость поворота ОАВ отпадает, и момент можно определять как скалярную алгебраическую величину, равную 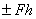 , где знак указывает направление поворота.
, где знак указывает направление поворота.
Но в случае сил, произвольно расположенных в пространстве, плоскости поворота у разных сил будут разными и должны задаваться дополнительно. Положение плоскости в пространстве можно задать, задав отрезок (вектор), перпендикулярный к этой плоскости. Если одновременно модуль этого вектора выбрать равным модулю момента силы и условиться направлять этот вектор так, чтобы его направление определяло направление поворота силы, то такой вектор полностью определит все три элемента, характеризующие момент данной силы относительно центра О.
Поэтому в общем случае момент  ) силы
) силы 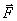 относительно центра О (рис. 37) будем изображать приложенным в центре О вектором
относительно центра О (рис. 37) будем изображать приложенным в центре О вектором 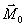 , равным по модулю (в выбранном масштабе) произведению модуля силы
, равным по модулю (в выбранном масштабе) произведению модуля силы 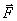 на плечо h и перпендикулярным к плоскости ОАВ, проходящей через центр О и силу
на плечо h и перпендикулярным к плоскости ОАВ, проходящей через центр О и силу 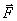 . Направлять вектор
. Направлять вектор 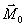 будем в ту сторону, откуда поворот, совершаемый силой, виден происходящим против хода часовой стрелки. Таким образом, вектор
будем в ту сторону, откуда поворот, совершаемый силой, виден происходящим против хода часовой стрелки. Таким образом, вектор 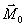 будет одновременно характеризовать модуль момента, плоскость поворота ОАВ, разную для разных сил, и направление поворота в этой плоскости. Точка приложения вектора
будет одновременно характеризовать модуль момента, плоскость поворота ОАВ, разную для разных сил, и направление поворота в этой плоскости. Точка приложения вектора 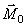 определяет положение центра момента.
определяет положение центра момента.
2. Выражение момента силы с помощью векторного произведения. Рассмотрим векторное произведение 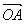 x
x 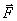 векторов
векторов 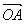 и
и 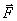 (рис. 37). По определению,
(рис. 37). По определению, 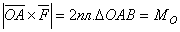 ,
,
так как модуль вектора 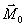 тоже равен 2 пл.
тоже равен 2 пл. 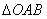 . Направлен вектор (
. Направлен вектор (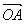 x
x 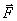 ) перпендикулярно к плоскости ОАВ, в ту сторону, откуда кратчайшее совмещение
) перпендикулярно к плоскости ОАВ, в ту сторону, откуда кратчайшее совмещение 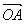 с
с 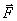 (если их отложить от одной точки) видно против хода часовой стрелки, т. е., так же, как вектор
(если их отложить от одной точки) видно против хода часовой стрелки, т. е., так же, как вектор 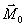 . Следовательно, векторы (
. Следовательно, векторы (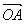 x
x 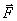 ) и
) и 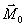 совпадают и по модулю и по направлению и, как легко проверить, по размерности, т. е. оба эти вектора изображают одну и ту же величину. Отсюда
совпадают и по модулю и по направлению и, как легко проверить, по размерности, т. е. оба эти вектора изображают одну и ту же величину. Отсюда
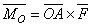 или
или  ,
,
где вектор  =
= 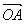 называется радиусом-вектором точки А относительно центра О.
называется радиусом-вектором точки А относительно центра О.
Таким образом, момент силы 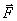 относительно центра О равен векторному произведению радиуса вектора
относительно центра О равен векторному произведению радиуса вектора  , соединяющего центр О с точкой приложения силы А, на саму силу. Этим выражением момента силы бывает удобно пользоваться при доказательстве некоторых теорем.
, соединяющего центр О с точкой приложения силы А, на саму силу. Этим выражением момента силы бывает удобно пользоваться при доказательстве некоторых теорем.


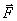 относительно центра О (см. рис. 37) как характеристика ее вращательного эффекта определяется следующими тремя элементами:
относительно центра О (см. рис. 37) как характеристика ее вращательного эффекта определяется следующими тремя элементами: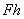 ; 2) плоскостью поворота ОАВ, проходящей через линию действия силы
; 2) плоскостью поворота ОАВ, проходящей через линию действия силы 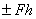 , где знак указывает направление поворота.
, где знак указывает направление поворота. ) силы
) силы 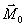 , равным по модулю (в выбранном масштабе) произведению модуля силы
, равным по модулю (в выбранном масштабе) произведению модуля силы 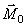 определяет положение центра момента.
определяет положение центра момента.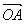 x
x 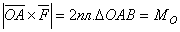 ,
,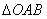 . Направлен вектор (
. Направлен вектор (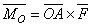 или
или  ,
, =
=  , соединяющего центр О с точкой приложения силы А, на саму силу. Этим выражением момента силы бывает удобно пользоваться при доказательстве некоторых теорем.
, соединяющего центр О с точкой приложения силы А, на саму силу. Этим выражением момента силы бывает удобно пользоваться при доказательстве некоторых теорем.


