Лист 4. Пересечение плоскостей
Согласно варианту построить: - проекции двух треугольников; - определить видимость сторон; - линию пересечения треугольников; - натуральную величину одного из треугольников. На чертеже Пересечение плоскостей студент учится графическому решению позиционных задач. Под позиционными понимаются задачи, решение которых позволяет получить ответ о принадлежности элемента (точки) или подмножества (линии) множеству (поверхности). К позиционным относят также задачи на определение общих элементов, принадлежащих различным геометрическим фигурам. Данные для позиционной задачи представлены в таблице 5. Линию пересечения заданных плоскостей можно найти: - используя вспомогательные секущие плоскости; - дважды применив решение задачи на пересечение прямой с плоскостью; - применив способ замены плоскостей проекции, введя новую плоскость проекций, перпендикулярную к одной из заданных плоскостей. Первый вариант решения обычно применяется тогда, когда проекции прямых, задающих плоскости на чертеже, не пересекаются. При этом используются плоскости уровня. Третий вариант в ряде случаев увеличивает число графических построений на чертеже. Решение необходимо выполнить по второму варианту. Для построения линии пересечения двух плоскостей необходимо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям. Эти точки определяют линию пересечения плоскостей. Пример выполнения листа Пересечение плоскостей представлен на рисунке А.3. Алгоритм решения: 1. Методом конкурирующих точек определить две стороны, участвующие в пересечении. На рисунке А.3 такими сторонами являются АВ и KD. Далее найти точку пересечения стороны АВ с плоскостью треугольника DEK. 2. Сторону АВ заключить во вспомогательную горизонтально-проецирующую плоскость 3. Найти линию пересечения плоскостей 4. Прямые AB и 2–6 лежат в одной вспомогательной плоскости 5. Аналогично, используя горизонтально проецирующую плоскость 6. Соединив одноимённые проекции точек M и N, определить горизонтальную (M /N /)и фронтальную (M //N //)проекции линии пересечения треугольников. 7. Видимость сторон треугольников определить способом конкурирующих точек. Видимые отрезки сторон треугольников выделить сплошными контурными линиями, невидимые следует показать штриховыми и тонкими линиями. Натуральную величину треугольника АВС можно найти: - методом прямоугольного треугольника; - способом замены плоскостей; - способами плоскопараллельного перемещения. Определение натуральной величины необходимо выполнить по первому варианту. Для этого следует методом прямоугольного треугольника последовательно определить натуральную величину каждой стороны треугольника АВС. Зная натуральную величину сторон А/В 0, В/С 0, С/А 0, на свободном поле листа можно построить натуральную величину треугольника АВС. Таблица 5
|

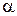 . Через фронтальную проекцию стороны А// В// провести фронтальный след фронтально проецирующей плоскости
. Через фронтальную проекцию стороны А// В// провести фронтальный след фронтально проецирующей плоскости 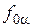 , тогда
, тогда 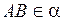 .
.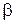 , определить точку пересечения стороны KD с плоскостью треугольника ABC (точка М).
, определить точку пересечения стороны KD с плоскостью треугольника ABC (точка М).


