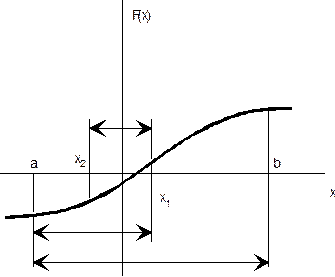Метод половинного деления (бисекции, дихотомии) является более устойчивым, чем рассмотренные выше. Существо его состоит в следующем.
Предполагается, что на отрезке [a, b] уравнение (1) имеет только один корень. Тогда F(a) и F(b) имеют разные знаки. Вычисляется первое приближение x0 как полусумма крайних значений a и b. Значение x0 делит отрезок [a, b] на две части, на одной из которых (поскольку корень единственный) функция F(x) меняет знак.
Допустим, что это отрезок [a, x0]. Вычисляем следующее приближение как полусумму a и x0. Приближение x1 делит в свою очередь отрезок [a, x0] на две части. Выбираем ту из них, на которой F(x) меняет знак и т.д. В конечном итоге получается последовательность интервалов, длина которых постепенно стягивается в точку. При этом центр интервала все более и более точно приближается к истинному значению корня.
Геометрическая интерпретация метода бисекции представлена на рис. 4.
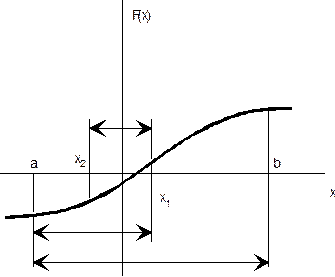
Рис.4