Роль математики в физике
Математика играет исключительно важную роль в физике. Математика дает самую высокую степень обобщения знаний. Благодаря этому она позволяет выразить законы физики в точной лаконичной форме. Физические законы, выраженные формулами и графиками, показывают вид функциональной зависимости величин, дают самую точную характеристику этой зависимости. Связь величин, выраженная математической формулой, позволяет получать теоретические выводы, которые после интерпретации, истолкования и выяснения смысла дают новые «выводные» знания. Путем преобразования математических выражений можно делать строгие логические выводы, на основе которых можно до опыта объяснять и предсказывать новые явления. Формулу, полученную экспериментально, приняв за аксиому, можно преобразовывать и получать следствия, которые могут служить для предвидения и объяснения новых явлений. Например, из экспериментального установления прямой пропорциональной зависимости Преобразование формул, выражающих эмпирические законы, и интерпретация полученных выражений нередко приводит к теоретическим открытиям. Например, исходя из закона движения планет, открытого Кеплером, Ньютон выдвинул гипотезу, согласно которой сила, удерживающая Луну на ее орбите, и сила, заставляющая падать камень на поверхность Земли с ускорением свободного падения, – это силы одной природы – силы гравитационного притяжения. Расчеты подтвердили правильность этого предположения. Так был открыт закон всемирного тяготения. По графику функции, которая является математическим выражением закона, часто можно интерпретировать, объяснить найденную зависимость величин. Например, зависимость координаты х от времени t при равномерном движении прямо пропорциональная, линейная. Следовательно, графиком, выражающим эту зависимость, является наклонная прямая линия. Наклон графика, определяемый выражением В некоторых случаях физическую величину можно вычислить по площади, ограниченной графиком, например, пройденный путь по графику скорости равномерного движения, потенциальную энергию пружины по ее деформации и др.
|

 между модулем силы упругой деформации F и самой деформацией х следует, что упруго деформированное тело обладает потенциальной энергией
между модулем силы упругой деформации F и самой деформацией х следует, что упруго деформированное тело обладает потенциальной энергией 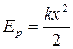 . Если изготовить пружинный пистолет, то заранее можно рассчитать, например, с какой скоростью вылетит из него шарик при выстреле.
. Если изготовить пружинный пистолет, то заранее можно рассчитать, например, с какой скоростью вылетит из него шарик при выстреле. , характеризует быстроту изменения функции х по отношению к изменению аргумента t. В частности, при равномерном движении угол наклона графика постоянен и
, характеризует быстроту изменения функции х по отношению к изменению аргумента t. В частности, при равномерном движении угол наклона графика постоянен и  равен модулю скорости движения:
равен модулю скорости движения:  . Аналогично по наклону графика скорости определяется модуль ускорения:
. Аналогично по наклону графика скорости определяется модуль ускорения:  .
.


